6.6. Примеры решения задач по квантовой оптике

Пример 1. Железный шар диаметром d = 0,1 м, нагретый до температуры Т₁=1500К, остывает на открытом воздухе. Через какое время его температура понизится до Т₂ = 1000 К? При расчете принять, что шар излучает как серое тело с коэффициентом излучения  = 0,5. Теплопроводностью воздуха пренебречь.

Решение

Количество теплоты, теряемое шаром при понижении температуры на малую величину dT, равно

dQ = c m dT, (1)

где c – удельная теплопроводность железа; m – масса шара.

Учитывая, что

m =  V= 4/3   r³, (2)

где r – радиус шара;  - плотность железа, получаем

dQ= 4/3  r³ c dT, (3)

С другой стороны, количество теплоты, теряемое шаром вследствие излучения, можно найти, используя закон Стефана-Больцмана:

dQ=   T⁴ S dt =   T⁴ 4  r² dt, (4)

где dt – время излучения, соответствующее понижению температуры на dT. Приравнивая правые части равенств (3) и (4), получаем

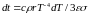. (5)

Проинтегрировав это выражение, найдем

t= c r(1/T₂³ – 1/T₁³)/ 3. (6)

После подстановки числовых значений получим t = 500 с.

Пример 2. Вследствие изменения температуры черного тела максимум спектральной плотности энергети- ческой светимости сместился с длины волны ₁ = 2,4 мкм на ₂ = 0,8 мкм. Как и во сколько раз изменилась энергетическая светимость тела и максимальная спектральная плотность энергетической светимости?

Решение

Зная длины волн, на которые приходятся максимумы лучеиспускательной способности тела, и, используя закон смещения Вина, находим начальную и конечную температуры тела

T

₁= b/ ₁, T₂= b/ ₂ .

Энергетическая светимость черного тела определяется согласно закону Стефана-Больцмана

R^*=  T⁴ ,

следовательно, R₁^*/ R₂^* = (T₂/T₁)⁴ = (₁/₂)⁴ .

Максимальное значение спектральной плотности энергетической светимости определяется по второму закону Вина

r^*_{ Tmax} = c T⁵ .

Тогда r^*_2max/ r^*_1max = (T₂/T₁)⁵ = (₁/₂)⁵ .

Подставляя числовые значения, получаем

R₂*/R₁* = 81;

r^*_2max/ r^*_1max = 243.

Пример 3. Красная граница фотоэффекта у рубидия равна ₀ =0,8мкм. Определить максимальную скорость фото- электронов при облучении рубидия монохроматическим светом с длиной волны  = 0,4 мкм. Какую задерживающую разность потенциалов нужно приложить к фотоэлементу, чтобы прекратился ток?

Решение

Энергия фотона вычисляется по формуле  =hc/ и составляет для  = 0,4 мкм  = 3,1 эВ. Эта величина значительно меньше энергии покоя электрона, поэтому максимальная кинетическая энергия фотоэлектрона может быть выражена классической формулой T_max= ½ mV_max². Выразив работу выхода через красную границу фотоэффекта, на основании уравнения Эйнштейна получим

T_max= ½ m V_max² = h c/  - h c/ ₀ .

Откуда

V_max= (2 h c(₀ - )/(m ₀ ))^1/2 .

Подставив числовые значения, найдем V_max= 0,7410⁸ м/с.

При U<0 внешнее поле между катодом и анодом фотоэлемента тормозит движение электронов. Задерживающая разность потенциалов Uз, при которой сила тока обращается в нуль, определится из уравнения e U_з =m V_max² /2.

Следовательно, U_з= hc(1/ - 1/₀) /e = 1,58 В.

Пример 4. Уединенный медный шарик облучают ультра- фиолетовыми излучением с длиной волны  = 165 нм. До какого максимального потенциала зарядится шарик?