6.4. Масса и импульс фотона. Давление света

Согласно гипотезе Эйнштейна свет испускается и поглощается в виде отдельных порций энергии - фотонов, которые можно рассматривать как частицы. Помимо энергии, фотон обладает и другими характеристиками, свойственными частице – массой и импульсом.

Массу фотона можно определить из закона пропор- циональности массы и энергии, установленного Эйнштейном

. (6.16)

Зная массу и скорость, определяем импульс:

. (6.17)

Таким образом, все корпускулярные характеристики фотона связаны с волновой характеристикой излучения - его частотой (длиной волны).

Корпускулярные свойства света позволяют достаточно просто объяснить световое давление как результат передачи импульса фотона отражающей или поглощающей поверх- ности. Пусть на поверхность с коэффициентом отражения  падает нормально монохроматический свет частоты . Давление равно суммарному импульсу, переданному единице площади поверхности в единицу времени:

. (6.18)

Если за единицу времени на единицу площади поверхности падает N фотонов, то из них N отражается и (1-)N поглощается. Каждый отраженный фотон передает поверхности импульс 2P_ф, поглощенный - P_ф. Тогда давление света равно:

.

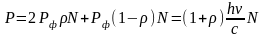Учитывая, что E = N h – есть энергия всех фотонов, а  = E/c – объемная плотность энергии излучения, получим

. (6.19)

Эта формула совпадает с выражением, полученным на основе электромагнитной теории света, т.е. световое давление одинаково успешно объясняется и волновой и квантовой теорией.

6.5. Эффект Комптона

В 1923 г. американский физик Комптон исследовал рассеяние монохроматического рентгеновского излучения легкими веществами (графит, парафин, бор и др.). Было установлено, что в рассеянном излучении, помимо исходного, присутствует излучение с большей длиной волны, причем длина волны растет с увеличением угла рассеяния. Это противоречит волновым представлениям о природе света: с позиций электромагнитной теории - при рассеянии на веществе длина волны не должна изменяться.

Эффект Комптона объясняется на основе квантовых представлений о взаимодействии фотонов с электронами. Один из видов такого взаимодействия рассматривался при обсуждении явления фотоэффекта: фотон исчезает, отдавая свою энергию электрону. При этом следует учитывать, что электрон в металле является связанным с другими электронами и ионами кристаллической решетки.

При взаимодействии фотона со свободным электроном может произойти только процесс рассеяния, в результате которого появится новый фотон, летящий под углом  к направлению движения первоначального фотона (рис.6.4) Законы сохранения следует записывать с учетом релятивистских эффектов в виде:

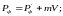
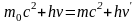. (6.20)

Здесь P_ф ,  и P’_ф , ' – импульс и частота фотона соответственно до взаимодействия и после.

Решение этих уравнений приводит к следующему выражению, определяющему изменение длины волны излучения при рассеянии на свободных электронах:

 = ^’ -  = (h/m₀c)(1 – cos) = _к(1 – cos), (6.21)

Рис.6.4

где _к = h / m₀ c = 2,43 пм – комптоновская длина волны,  - угол рассеяния фотонов.

Полученная формула соответствует экспериментально установленной зависимости длины волны рассеянного излучения от угла рассеяния. Рассеяние света на тяжёлых веществах происходит без изменения длины волны. Это объясняется взаимодействием фотонов с сильно связанными электронами: фотон упруго взаимодействует со всем атомом, масса которого гораздо больше, поэтому практически не передает ему энергии.