5.5. Примеры решения задач по волновой оптике

Пример 1. На зеркала Френеля, угол между которыми  = 10', падает монохромати­ческий свет от узкой щели S, находящейся на расстоянии r = 0,1 м от линии их пересечения Отраженный от зеркал свет дает интерференционную кар­тину на экране Э, отстоящем на расcтоянии а =2,7м от линии их пересечения, причем расстояние между интерференционными полосами равно х = 2,9 · 10^-11 м. Определить длину волны λ света.

Решение

После отражения от зеркал OK, OL световые волны распространяются так, будто вышли из двух когерентных источников S₁ и S₂, являющихся мнимыми изображениями щели S. Пусть расстояние между источниками S₁ и S₂, равно d, а расстояние от них до экрана l. Величины l, d, x,  связаны соотно­шением

λ = xd/l. (1)

Чтобы найти d и l, учтем, что точки S₁ и S₂ симметричны точке S относительно соответствующих зеркал. Поэтому S₁O = S₂O = r и S₁OS₂ = 2α. Так как угол α весьма мал и экран обычно распо­лагается параллельно отрезку S₁S₂, то можно записать:

d = 2r, l = r + а.

Подставив эти значения d ,l в формулу (1), получим

λ = 2rx/(r + а).

После подстановки числовых значений величин (предварительно выразив угол α в радианах) найдем

 = 6  10^-7 м = 0,6 мкм.

Пример 2. Для уменьшения потерь света при отражении от стекла на поверхность объектива (n₂ = 1,7) нанесена тонкая прозрачная пленка (n = 1,3). При какой на­именьшей толщине ее произойдет максимальное ослаб­ление отраженного света, длина волны которого при­ходится на среднюю часть видимого спектра (λ₀ = 0,56 мкм)? Считать, что лучи падают нормально к поверхности объектива.

Решение

Свет, падая на объектив, отражается как от перед­ней, так и от задней поверхностей тонкой пленки. Отраженные лучи интерферируют. Условие минимума интенсивности света при интерференции выражается формулой

.

Оптическая разность хода лучей, отраженных от двух поверхно­стей тонкой пленки, окруженной одинаковыми средами, определяется формулой

 = 2hn cos - ₀/2.

В данном случае пленка окружена различными сре­дами - воздухом (n₁ = 1,0) и стеклом (n₂ = 1,7). Из неравенства n₁ < n < n₂ следует, что оба луча 1 и 2, отражаясь от границы с оп­тически более плотной средой, «теряют» полуволну. Так как это не влияет на их разность хода, то следует отбросить слагаемое λ₀/2. Кроме того, полагая  = 0, получим

Δ = 2hn.

Тогда толщина пленки

h = (2k + 1)₀/4n.

Учитывая, что h - существенно положительная величина и что значению h_min соответствует k = 0, получим

h_min = λ₀/4n = 0,11 мкм.

Пример 3. Между двумя плоскопараллельными стеклян- ными пластинками заключен очень тонкий воздушный клин. На пластинки нормально падает монохроматический свет (λ₀ = 0,50 мкм). Определить угол  между пластинками, если в отраженном свете на протяжении l = 1,00 см наблюдается N = 20 интерференционных полос.

Решение

В данном случае интерферируют лучи 1 и 2, отражен­ные от двух поверхностей тонкого воздушного клина (см. рис.). Наблюдаемые на поверхности клина интерференционные полосы будут полосами равной толщины, пред­ставляя собой геометрическое место точек, соответствующих одинаковой толщине клина.

Пусть точки А, В соответствуют двум соседним интерференцион­ным полосам. Проведя прямую ВС, парал- лельную нижней пластинке, и учитывая, что искомый угол весьма мал, имеем

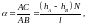(1)

где h_A, h_B — толщины воздушного клина в точках А, В.

Предпо­ложим для определенности, что АВ — расстояние между тем­ными интерференционными полосами. Тогда обе величины h_A, h_B най­дем, приравняв правые части формул и . Так как i₂ = 0, n = 1 (воздух) и h > 0, то

(2)

h = (k + 1) λ_0./2.

Поскольку величины h_A, h_B относятся к соседним полосам, то в фор­муле (2) числа k, соответствующие величи- нам h_A, h_B должны отли­чаться на единицу. Следовательно,

(3)

.

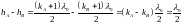Легко, убедиться, что к такому же результату придем, предполо­жив, что АВ есть расстояние между соседними светлыми полосами. Теперь из формулы (1) с учетом результата (3) найдем

 = ₀N/2l = 510^-4 рад = 140.

Пример 4. Сферическая поверхность плосковыпуклой линзы (n₁ = 1,52) соприкасается со стеклянной пластинкой (n₂ = 1,7). Пространство между линзой, радиус кри­визны которой R = 1 м, и пластинкой заполнено жидкостью. Наблю- дая кольца Ньютона в отраженном свете (λ₀ = 0,589 мкм), измерили радиус r_k десятого тем­ного кольца. Определить показатель преломления жид­кости n_ж в двух случаях:

1) r_k = 2,05 мм, 2) r_k = 1,9 мм.