2.6. Примеры решения задач по законам электромагнитной индукции

Пример 1. В однородном магнитном поле (В = 0,2Тл) равномерно с частотой ν = 600 мин^-1 вращается рамка, содержащая N = 1200 витков, плотно прилегающих друг к другу. Площадь рамки S = 100 см². Ось вращения лежит в плоскости рамки и перпендикулярна линиям магнитной индукции. Определите максимальную ЭДС, индуцируемую в рамке.

Решение

Согласно закону электромагнитной индукции

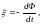
где Ф = NBScos α – полный магнитный поток, пронизывающий рамку.

ν

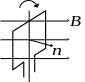При вращении рамки угол 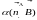, образованный нормалью n к плоскости рамки и линиями индукции В, изменятся по закону

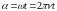
Подставив в закон электромагнит- ной индукции выражение магнит- ного потока и продифференцировав по времени, найдем мгновенное значение ЭДС индукции:

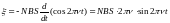
Максимальное значение ЭДС определится при условии, что sin 2πνt =1. таким образом,

.

Убедимся в том, что правая часть этого равенства дает единицу ЭДС (В):

Произведем вычисление:

.

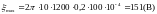Пример 2. Соленоид содержит N =1200 витков прово- да, плотно прилегающих друг к другу. При силе тока I = 4 A магнитный поток Ф = 6 мкВб. Определить индуктивность L соленоида и энергию магнитного поля соленоида.

Решение

Индуктивность L связана с потокосцеплением Ψ = LI.

Потокосцепление, в свою очередь, может быть определено через поток Ф и число витков N:

Ψ = NФ.

На основании этих формул индуктивность соленоида

.

Энергия магнитного поля соленоида

Подставим в формулы для L и W значения физических величин и произведем вычисления:

.

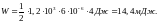Пример 3. Определить индукцию В и напряжённость Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N = 200 витков, идёт ток I =5 А. Внеш- ний диаметр d₁ тороида равен 30 см, внутренний d₂ = 20 см.

Решение

Для определения напряжённости магнитного поля внутри тороида вычислим циркуляцию вектора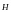 вдоль линий магнитной индукции поля: .

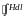Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и что во всех точках этой линии напряжённости одинаковы. Поэтому в выражении циркуляции напряжённость Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2πr, где r-радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т.е.

. (1)

С другой стороны, в соответствии с законом полного тока циркуляция вектора напряжённости магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция:

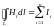. (2)

Приравняв правые части равенств (1) и (2) получим

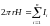. (3)

Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2πrН = NI, откуда

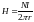. (4)

Для средней линии тороида r = (R₁+ R₂)/2= (d₁+ d₂)/4. Подставив выражение в формулу (4), найдём

. (5)

Магнитная индукция В₀ в вакууме связана с напряжённостью поля соотношением В₀=μ₀Н. Следовательно,

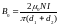. (6)

Подставив значения величин в выражения (5) и (6), получим: Н =1,37 кА/м, В₀ =1,6 мТл.

Пример 4. Чугунное кольцо имеет воздушный зазор длиной l₀ = 5мм. Длина l средней линии кольца равна 1 м. Сколько витков N содержит обмотка на кольце, если при силе тока I = 4А индукция В магнитного поля в воздушном зазоре равна 0,5 Тл. Рассеянием магнитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать.