2.2. Явление самоиндукции. Индуктивность соленоида

Электромагнитная индукция наблюдается во всех случаях, когда изменяется магнитный поток сквозь контур. Если в некотором контуре течет изменяющийся ток, то магнитное поле тока также будет изменяться. Это повлечет изменение магнитного потока через контур и, следовательно, появление ЭДС индукции. Данное явление называется самоиндукцией.

Если в пространстве, где находится контур с током, нет ферромагнетиков, то в соответствии с законом Био-Савара величина магнитной индукции B и полный магнитный поток  будут пропорциональны силе тока. Это позволяет написать

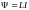. ( 2.7)

Коэффициент пропорциональности L называется индуктивностью контура. Единица индуктивности в СИ называется Генри:

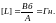
Индуктивность L зависит от геометрии контура и магнитных свойств окружающей среды.

Вычислим индуктивность соленоида. При протекании по соленоиду тока внутри него возбуждается магнитное поле, индукция которого равна

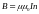, (2.8)

где n = N/l – плотность витков.

Полный магнитный поток при этом будет

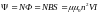, (2.9)

где l – длина соленоида, S – площадь поперечного сечения, а V- его объем.

Таким образом, индуктивность соленоида

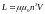. (2.10)

При изменениях силы тока I в контуре возникает ЭДС самоиндукции, равная

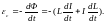
Если L = const, то

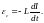(2.11)

Знак минус показывает, что ЭДС самоиндукции всегда направлена так, чтобы препятствовать изменению силы тока в соответствии с правилом Ленца.

Характерные проявления самоиндукции – экстратоки, возникающие при замыкании и размыкании электрических цепей с индуктивностью.

2.3. Расчёт токов при замыкании и размыкании цепей с индуктивностью

1. Исчезновение тока при размыкании цепи

Пусть цепь состоит из катушки с индуктивностью L, резистора сопротивлением R, источника ЭДС и ключа К (рис.2.2). Когда ключ К находится в позиции 1, в цепи течет ток I = ξ /R (r<<R). В момент t = 0 ключ перебрасывается в позицию 2.

Т ок в цепи начнет убывать и возникнет ЭДС самоиндукции, противодействующая убыванию тока. По закону Ома

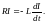(2.12)

Рис.2.2

При интегрировании уравне- ния по току от I₀ до I и по времени от 0 до t, получим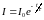

. (2.13)

где  = L/R – постоянная времени, называемая временем релаксации. Зависимость I(t) представлена кривой 1 на рис.2.3.

2. Установление тока при замыкании цепи

В момент t = 0 ключ К повернем в позицию 1 и тем самым к индуктивности подключим источник ЭДС. Ток в цепи начнет нарастать и снова возникнет ЭДС самоиндукции. По закону Ома

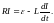(2.14)

Интегрируя по t уравнение (2.14), получим

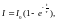(2.15)

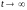г де I₀ - установившийся ток (при ). График зависимости I(t) представлен кривой 2 на рис. 2.3.