
- •Часть 1
- •Часть 1
- •Введение
- •1. Основные понятия теории графов
- •Задачи теории графов
- •1.2. Основные определения
- •1.3. Степени вершин графа
- •1.4. Изоморфизм графов
- •2. Представление графов в эвм и операции над ними
- •2.1. Матричные способы задания графов
- •2.2. Список ребер (луг) и структура смежности графа
- •2.3. Части графов
- •2.4. Основные операции над графами
- •3. Маршруты в графах
- •3.1. Понятие маршрута
- •Маршруты в неориентированных графах
- •Маршруты в ориентированных графах
- •3.2. Связность в графах.
- •В примере 3 граф имеет две сильно связных компоненты.
- •3.3. Связность и матрица смежности графа
- •3.4. Матрица взаимодостижимости
- •4. Деревья
- •4.1. Свободные деревья
- •4.2. Ориентированные, упорядоченные и бинарные деревья
- •Эквивалентное определение ориентированного дерева
- •5. Эйлеровы и гамильтоновы графы.
- •5.1. Эйлеровы графы.
- •5. 2. Алгоритм построения эйлерова цикла в эйлеровом графе
- •5.3. Гамильтоновы графы
- •5.4. Оценки числа эйлеровых и гамильтоновых графов
- •6. Фундаментальные циклы и разрезы
- •6.1. Фундаментальные циклы
- •6.2. Разрезы
- •7. Связь теории графов с бинарными отношениями и векторными пространствами
- •7.1. Отношения на множествах и графы
- •7.2. Векторные пространства, связанные с графами
- •8. Планарность и раскраска графов
- •8.1. Планарные графы
- •8.2. Раскраска графов
- •8.3. Алгоритм последовательной раскраски
- •9. Покрытия и независимость
- •9.1. Покрывающие множества вершин и ребер
- •9.2. Независимые множества вершин и ребер
- •9.3. Доминирующие множества
- •10. Кратчайшие маршруты в графах
- •10.1. Расстояния в графах
- •10.2. Алгоритм Форда-Беллмана
- •11. Задача коммивояжера
- •11.1. Постановка задачи
- •11.2. Обходы вершин графа по глубине и ширине
- •11.3. Решение задачи коммивояжера
- •12. Потоки в сетях
- •12.1. Основные определения
- •12.2. Теорема Форда и Фалкерсона
- •12.3. Алгоритм построения максимального потока
- •13. Сетевое планирование и управление
- •13.1. Элементы сетевого графика
- •13.2. Временные параметры сетевого графика
- •13.3. Распределение ограниченных ресурсов
- •14. Анализ технических систем (на примере электрической цепи)
- •14.1 Закон Кирхгофа
- •14.2. Основные уравнения
- •15. Сигнальные графы
- •15.1. Общие представления о сигнальных графах
- •15.2. Преобразования сигнальных графов
- •15.3. Формула Мэзона
- •16. Переключательные сети (схемы)
- •17. Математические машины и цепи маркова
- •Библиографический список
- •Оглавление
- •Часть 1
- •394026 Воронеж, Московский просп., 14
5. Эйлеровы и гамильтоновы графы.
5.1. Эйлеровы графы.
 Содержательная
постановка задачи о Кенигсбергских
мостах дана в теме 1. Переформулируем
эту задачу в терминах теории графов.
Для этого рассмотрим следующий
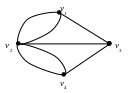
неориентированный мультиграф:
Содержательная
постановка задачи о Кенигсбергских
мостах дана в теме 1. Переформулируем
эту задачу в терминах теории графов.
Для этого рассмотрим следующий
неориентированный мультиграф:
Рис. 18
В этом графе вершины v1 и v4 соответствуют берегам, а v2 и v3 – островам. Ребра отображают мосты. Таким образом, на языке теории графов исходная задача формулируется следующим образом: существует ли в указанном мультиграфе цикл, содержащий все ребра данного мультиграфа?
Определение: Цепь (цикл), содержащая все ребра графа и притом по одному разу, называется эйлеровой цепью (эйлеровым циклом). Граф, содержащий эйлеров цикл, называется эйлеровым грфом.
Теорема. Для того, чтобы конечный связный неориентированный мультиграф был эйлеровым необходимо и достаточно, чтобы все его вершины имели чётные степени.
Д о к а з а т е л ь с т в о:
Необходимость. Предположим, что граф является эйлеровым. Это значит, что, в нём есть эйлеров чикл. При этом каждый раз, когда эйлеров цикл проходит через какую-либо вершину, он должен войти в нее по одному ребру, а выйти по другому. Следовательно, условие отсутствия вершин нечетной степени является необходимым.
Достаточность.
Предположим, что все вершины связного
графа G имеют
чётные степени. Тогда, в силу связности
графа G, для всех его
вершин выполняется условие d(v)>0.
Кроме того, в силу чётности вершин,
должно быть d(v)2
для всех v. По теореме
Эйлера имеем:![]() .Это
значит, что:
.Это
значит, что:![]() или
или
![]() ,
и следовательно граф G
не является деревом, а поэтому он содержит
хотя бы один простой цикл Z1
(Z1 - множество
ребер), тогда G\Z1
– остовный подграф, в котором все степени
вершин также четные. Исключим из
рассмотрения изолированные вершины,
тогда в графе G\Z1
существует простой цикл Z2G\Z1,
далее выделим Z3
и т.д. В результате этого получается
разбиение множества ребер на простые
циклы, то есть:
,
и следовательно граф G
не является деревом, а поэтому он содержит
хотя бы один простой цикл Z1
(Z1 - множество
ребер), тогда G\Z1
– остовный подграф, в котором все степени
вершин также четные. Исключим из
рассмотрения изолированные вершины,
тогда в графе G\Z1
существует простой цикл Z2G\Z1,
далее выделим Z3
и т.д. В результате этого получается
разбиение множества ребер на простые
циклы, то есть:![]() ,где
,где
![]() .
.
Далее,
возьмем какой либо простой цикл
![]() из полученного разбиения. Если
из полученного разбиения. Если
![]() ,
то теорема доказана. Если нет, то в силу
связности графа G,
существуют цикл
,
то теорема доказана. Если нет, то в силу
связности графа G,
существуют цикл
![]() и вершина v1
такие, что
и вершина v1
такие, что
![]() и
и
![]() .
Маршрут, объединяющий
и
.
Маршрут, объединяющий
и
![]() ,
является циклом. Если
,
является циклом. Если
![]() ,
то теорема доказана. Если нет, то имеется
чикл
,
то теорема доказана. Если нет, то имеется
чикл
![]() ,
при котором существует вершина v2
такая, что
,
при котором существует вершина v2
такая, что
![]() и
и
![]() .
Далее будем наращивать эйлеров цикл до
тех пор, пока не исчерпаем всё разбиение.
В результате получаем эйлеров цикл.
всего графа.
.
Далее будем наращивать эйлеров цикл до
тех пор, пока не исчерпаем всё разбиение.
В результате получаем эйлеров цикл.
всего графа.
5. 2. Алгоритм построения эйлерова цикла в эйлеровом графе
Этот алгоритм задается следующими правилами:
Выбирается произвольная вершина v.
Выбирается ребро e инцидентное вершине v и ему присваивается номер 1 (это ребро называется пройденным).
Каждое пройденное ребро вычеркивается и присваивается номер на 1 больший номера предыдущего вычеркнутого ребра.
При нахождении в произвольной вершине x, не выбирается ребро, соединяющее x с v, если есть возможность другого выбора.
Ребро не проходится, если оно является перешейком. Перешейк – это ребро, при удалении которого, граф, образованный невычеркнутыми ребрами, распадается на две компоненты связности, каждая из которых имеет хотя бы одно ребро.
После того, как в графе будут занумерованы все ребра, образуется эйлеров цикл, нумерация рёбер которого соответствует последовательности обхода ребер.
Пример. Найти эйлеров цикл в эйлеровом графе
П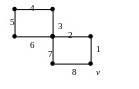 осле
выбора вершины v
и прохождения рёбер 1 и 2 имеется три
возможности: выбрать 3,6 или 7. Ребро 7
является пере-
осле
выбора вершины v
и прохождения рёбер 1 и 2 имеется три
возможности: выбрать 3,6 или 7. Ребро 7
является пере-
Рис. 19
шейком, поэтому выбирается любое из оставшихся рёбер, например 3. Далее идёт обход оставшихся рёбер получается эйлеров цикл.
