3. Маршруты в графах

3.1. Понятие маршрута

Маршрутом в графе G=(V,E) называется чередующаяся последовательность вершин и ребер (дуг) – v₁, e₁, v₂, e₂, …., v_n, e_n,v_n+1, в которой любые два соседних элемента инциденты.

Маршрут, соединяющий вершины v₁ и v_n+1 можно также задать последовательностью из одних вершин v₁, v₂, v₃,…,v_n, v_n+1 или последовательностью ребер e₁, e₂,…,e_n. Число n ребер (или дуг) в маршруте называется его длиной. Маршрут называется циклическим, если v₁=v_n+1.

Маршруты в неориентированных графах

Маршрут в неорграфе называется цепью, если все его ребра различны. Цепь называется простой, если все её вершины, кроме возможно первой и последней, различны. Циклическая цепь называется циклом, а простая циклическая цепь – простым циклом.

Неорграф без циклов называется ациклическим графом. Минимальная из длин циклов неорграфа называется его обхватом.

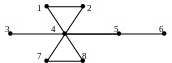
Пример 1: Рассмотрим неорграф

Рис. 9

В данном примере наборы вершин: (1,2); (1,2,4,7) являются простыми цепями,: (1,2,4,7,8,4) - непростая цепь, (1,2,4,7,8,4,2) – маршрут, который не является цепью, (1,2,4,8,4,1) – непростой цикл, (1,2,4,1) – простой цикл. Обхват графа равен 3.

Маршруты в ориентированных графах

Маршрут ориентированного графа называется путем, если все его дуги различны.

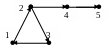Путь называется контуром, если v₁=v_n+1. Граф не имеющий контуров называется безконтурным. Вершина v называется достижимой из вершины u, если существует путь из u в v.

Пример 2: Рассмотрим ориентированный граф

Рис. 10

В данном примере наборы вершин (1,2,3,1) образуют контур. Заметим, что здесь вершина 5 – достигается из любой другой вершины, а из вершины 5 не достигается ни одна из остальных вершин.

3.2. Связность в графах.

Неорграф называется связным, если любые две его несовпадающие вершины соединены маршрутом. Граф называется связным, если соответствующий ему неорграф является связным. В данном случае соответствующий неориентированный граф получается из исходного графа путём замены всех его дуг рёбрами. Граф называется сильно связным, если для каждой пары различных вершин u и v существуют маршруты (u,v) и (v,u). Из этого определения следует, что любой связный неорграф является также сильно связным. Понятии связности и сильной связности распространяются также и на мультиграфы.

Отметим, что граф в примере 1 является сильно связным, а в приме2 – не сильно связный граф.

Пример 3. На следующем рисунке показан несвязный граф.

Р ис. 11

Всякий максимальный по включению сильно связный подграф данного графа называется его сильно связной компонентой, или сильной компонентой связности.

В примере 3 граф имеет две сильно связных компоненты.

3.3. Связность и матрица смежности графа

Теорема 1. Любой граф представляется в виде объединения непересекающихся (сильно) связных компонент. Разложение графа на (сильно) связные компоненты определяется однозначно.

Таким образом, множество вершин связных компонент, а также сильных компонент образуют разбиение множества вершин графа, причем число с(G) связных компонент графа G определяется однозначно.

Теорема 2. Если A матрица смежности графа G, то (i, j) элемент матрицы A^k=A·A·A·_·…·A (k раз), есть число (v_i, v_j) маршрутов длины k.

Следствие 1. В графе G мощности n тогда и только тогда существует маршрут (v_i, v_j) , причем v_i ≠v_j , когда (i, j) – элемент матрицы A+A²+ A³+ A⁴+…+ A^n-1 не равен нулю.

Следствие 2. В графе G мощности n тогда и только тогда существует цикл, содержащий вершину v_i когда (i, i) – элемент матрицы A+A²+ A³+ A⁴+…+ A^n-1+Aⁿ не равен нулю.

Пример. При помощи матрицы смежности определим существование всевозможных (1, 3) - маршрутов в графе, изо браженном на рисунке.

Рис. 12

П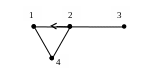 о графу находим матрицу смежности A:

A= .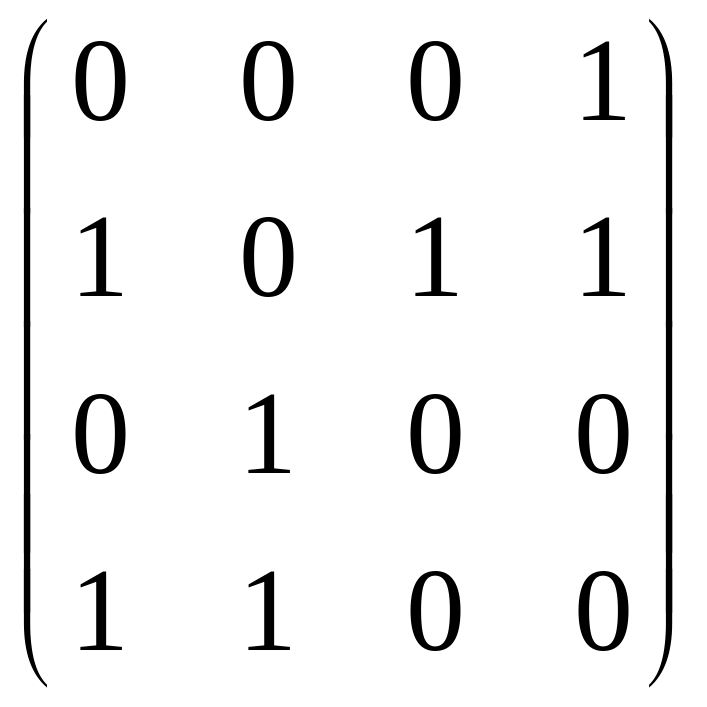

Её элемент (1,3)=0, следовательно. (1, 3) маршрутов длины 1 в графе нет. Затем находим:

A²= * = .

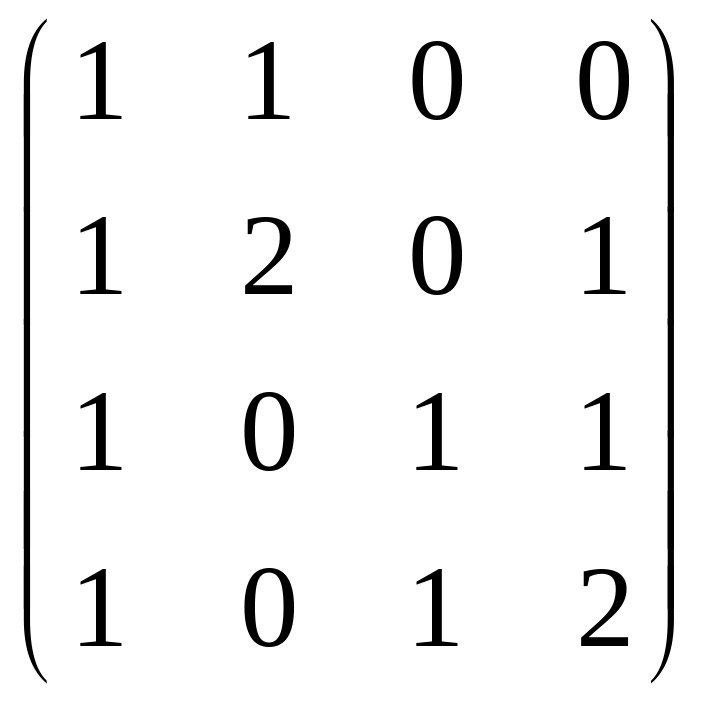В этой матрице элемент (1,3)=0, т.е. (1, 3) маршрута длины 2 в графе нет. Далее

A³= A²·A = · =

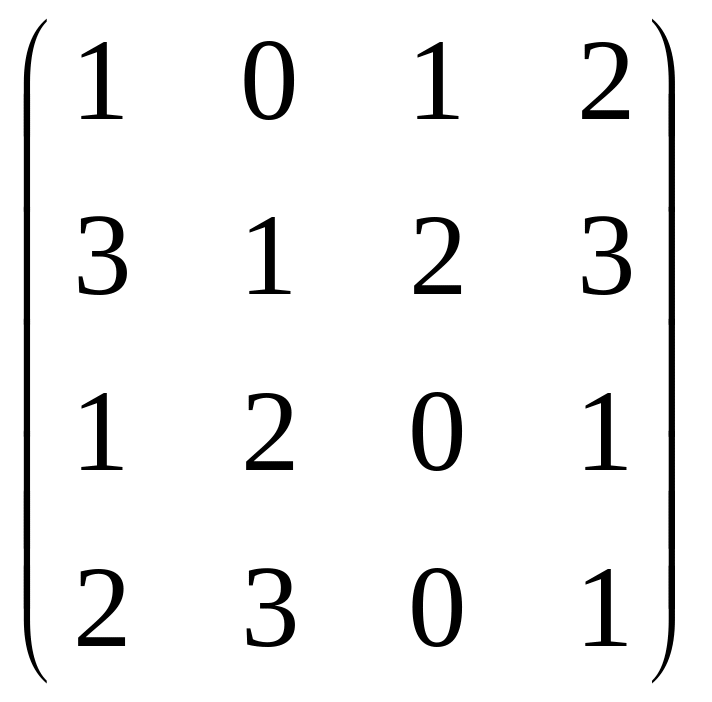
Eё элемент (1, 3)=1, т.е. существует ровно один (1, 3) - маршрут длины 3. Этот маршрут определяется набором вершин (1, 4, 2, 3)

Эту последовательность вершин можно найти на основе перемножения матрицы смежности: Элемент (1, 3) матрицы A³ получается при перемножении элемента (1, 2) матрицы A² на элемент (2, 3) матрицы A. В свою очередь элемент (1, 2) матрицы A² образуется при перемножении элемента (1, 4) матрицы A на элемент (4, 2) матрицы A, т.е. следовательно, двигаясь от 1 к 3 за 3 шага, получаем маршрут (1,4, 2, 3).

В матрице A³ элемент (4, 2) равен 3, это значит, что существуют три (4,2) маршрута длины 3 : (4, 1, 4, 2), (4, 2, 4, 2), (4, 2, 3, 2).