2.2. Список ребер (луг) и структура смежности графа

Если граф является разреженным, то есть когда число рёбер (дуг) m= много меньше числа вершин n= , то целесообразно представлять граф посредством списка рёбер (дуг). Этот список задается двумя наборами и , где - i-ая дуга графа.

Пример. Для графа, приведенного ранее, имеем:

и . Здесь для упрощения записи мы пишем 1 вместо , 2 - вместо и т.д.

Объём памяти для списка рёбер (дуг) – О(2m)

Представление графа, удобное при работе с графами, в которых добавляются или удаляются вершины, является структура смежности. Она получается путем составления для каждой вершины списка номеров вершин , для которых .

Пример. Для графа, представленного ранее, имеем:

Вершины	Список последовательностей
1	2,5,7
2	1,3,5,6
3	2,4
4	3,5,6
5	1,2,4
6	1,2,4

Объём памяти для структуры смежности – О(n+m)

2.3. Части графов

Подграфом графа называется граф , для которого и .

Полный подграф некоторого графа называется кликой этого графа.

Остовным подграфом графа называется подграф, содержащий все вершины исходного графа G, т.е. , где .

Порожденным подграфом графа на множестве вершин Vp называется граф Gp=(Vp, Ep), причем VpV ,а Ep – множество ребер или дуг графа G, оба конца которых принадлежат множеству Vp.

Пример. На следующем рисунке изображены:

а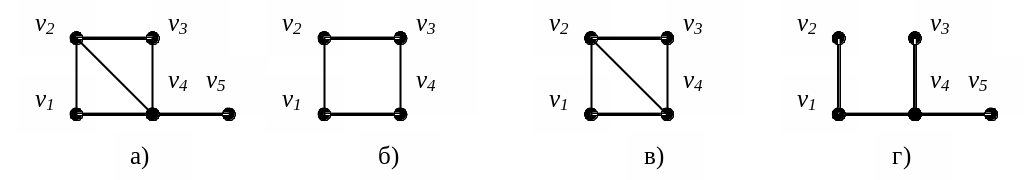 ) - исходный граф G, б) - один из его подграфов, в) - порождённый подграф графа G на множестве вершин , г) – один из остовных подграфов графа G.

Рис. 6

2.4. Основные операции над графами

Объединением графов G₁=(V₁, E₁) и G₂=(V₂, E₂) называется граф G₃=(V₁V₂, E₁E₂). Объединение называется дизъюнктным , если V₁V₂=0.

Пересечение графов G₁=(V₁, E₁) и G₂=(V₂, E₂) называется граф G₃=(V₁V₂, E₁E₂).

Аналогично определяется объединение, дизъюнктное объединение и пересечение любого количества графов. Операции объединения и пересечения являются коммутативными, т.е. G₁ G₂= G₂ G₁, а также G₁ G₂= G₂ G₁

Пример. На ниже приведённом рисунке показаны: а) – граф G₁, б) – граф G₂, в) – их объединение, г) – пересечение.

б)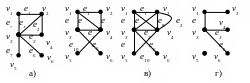

Удаление вершины. При удалении вершины из графа

Рис. 7

удаляются и все инцидентные ей рёбра (дуги).

Удаление ребра (дуги). При удалении ребра (дуги) его концевые вершины не удаляются. Операцией обратной к операции удаления ребра является операция добавления ребра.

Слияние (отождествление) вершин. Говорят, что вершины v_i и v_j в графе G отождествляются (сливаются) если они заменяются новой вершиной v_k такой, что все ребра (дуги) графа инцидентные v_i и v_j становятся инцидентными к вершине v_k .

Стягивание ребра – эта операция означает удаление ребра и отождествление его кольцевых вершин. Граф G называется стягиваемым графу Н, если граф Н может быть получен из G в результате некоторой последовательности стягиваний ребер.

Подразбиение ребра. При выполнении этой операции из графа удаляется ребро (v_i, v_j) и добавляются два новых (v_i, v_k) и (v_k, v_i), где v_k – новая вершина графа.

Пример:

На следующем рисунке представлены: а) - исходный граф, б) – граф после удаления вершины v₃, в) - результат удаления ребра e₂, г) –отождествления вершин v₃ и v₄, д) –стягивание ребра e₁, е) – подразбиение ребра e₂.

Р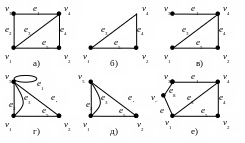 ис. 8