
- •Часть 1
- •Часть 1
- •Введение
- •1. Основные понятия теории графов
- •Задачи теории графов
- •1.2. Основные определения
- •1.3. Степени вершин графа
- •1.4. Изоморфизм графов
- •2. Представление графов в эвм и операции над ними
- •2.1. Матричные способы задания графов
- •2.2. Список ребер (луг) и структура смежности графа
- •2.3. Части графов
- •2.4. Основные операции над графами
- •3. Маршруты в графах
- •3.1. Понятие маршрута
- •Маршруты в неориентированных графах
- •Маршруты в ориентированных графах
- •3.2. Связность в графах.
- •В примере 3 граф имеет две сильно связных компоненты.
- •3.3. Связность и матрица смежности графа
- •3.4. Матрица взаимодостижимости
- •4. Деревья
- •4.1. Свободные деревья
- •4.2. Ориентированные, упорядоченные и бинарные деревья
- •Эквивалентное определение ориентированного дерева
- •5. Эйлеровы и гамильтоновы графы.
- •5.1. Эйлеровы графы.
- •5. 2. Алгоритм построения эйлерова цикла в эйлеровом графе
- •5.3. Гамильтоновы графы
- •5.4. Оценки числа эйлеровых и гамильтоновых графов
- •6. Фундаментальные циклы и разрезы
- •6.1. Фундаментальные циклы
- •6.2. Разрезы
- •7. Связь теории графов с бинарными отношениями и векторными пространствами
- •7.1. Отношения на множествах и графы
- •7.2. Векторные пространства, связанные с графами
- •8. Планарность и раскраска графов
- •8.1. Планарные графы
- •8.2. Раскраска графов
- •8.3. Алгоритм последовательной раскраски
- •9. Покрытия и независимость
- •9.1. Покрывающие множества вершин и ребер
- •9.2. Независимые множества вершин и ребер
- •9.3. Доминирующие множества
- •10. Кратчайшие маршруты в графах
- •10.1. Расстояния в графах
- •10.2. Алгоритм Форда-Беллмана
- •11. Задача коммивояжера
- •11.1. Постановка задачи
- •11.2. Обходы вершин графа по глубине и ширине
- •11.3. Решение задачи коммивояжера
- •12. Потоки в сетях
- •12.1. Основные определения
- •12.2. Теорема Форда и Фалкерсона
- •12.3. Алгоритм построения максимального потока
- •13. Сетевое планирование и управление
- •13.1. Элементы сетевого графика
- •13.2. Временные параметры сетевого графика
- •13.3. Распределение ограниченных ресурсов
- •14. Анализ технических систем (на примере электрической цепи)
- •14.1 Закон Кирхгофа
- •14.2. Основные уравнения
- •15. Сигнальные графы
- •15.1. Общие представления о сигнальных графах
- •15.2. Преобразования сигнальных графов
- •15.3. Формула Мэзона
- •16. Переключательные сети (схемы)
- •17. Математические машины и цепи маркова
- •Библиографический список
- •Оглавление
- •Часть 1
- •394026 Воронеж, Московский просп., 14
1.3. Степени вершин графа
Степенью (валентностью) (обозначение d(v) или deg(v)) вершины v простого графа G называется число ребер или дуг инцидентных данной вершине v. При подсчете валентности вершин псевдографа следует учитывать каждую петлю дважды.
Если степени всех вершин н-графа равны k, то граф называется регулярным (однородным) степени k. Если степень вершины равна 0, то она является изолированной. Если степень вершины равна 1, то вершина называется концевой (висячей, тупиковой).
Для
орграфа число дуг исходящих из вершины
v называется полустепенью исхода
![]() (v),
а входящих – полустепенью захода
(v),
а входящих – полустепенью захода
![]() (v),
При этом справедливо соотношение d(v)=
(v)+
(v).
(v),
При этом справедливо соотношение d(v)=
(v)+
(v).
Теорема
Эйлера: Сумма степеней вершин графа
равна удвоенному количеству ребер, т.е.
![]() ,
или
,
или
![]() ,
где n – число вершин; m – число
ребер (дуг). Данное утверждение доказывается
тем, что при подсчете суммы степеней
вершин каждое ребро учитывается два
раза - для одного конца ребра и для
другого.
,
где n – число вершин; m – число
ребер (дуг). Данное утверждение доказывается
тем, что при подсчете суммы степеней
вершин каждое ребро учитывается два
раза - для одного конца ребра и для
другого.
1.4. Изоморфизм графов
Граф называется
помеченным (или перенумерованным),
если его вершины отличаются друг от
друга какими либо пометками (номерами).
Граф считается полностью заданным в
строгом смысле, если нумерация его
вершин и ребер фиксирована. При этом
графы G1 и G2
называются равными (обозначение
G1 = G2), ,если
их множества вершин и ребер совпадают.
Два графа или псевдографа G1=(V1,E1)
и G2=(V2,E2)
называются изоморфными (обозначение
![]() ),
если существуют два взаимно однозначных
отображения: 1)
),
если существуют два взаимно однозначных
отображения: 1)
![]() и 2)
и 2)
![]() такие, что для любых двух вершин
такие, что для любых двух вершин
![]() в графе
в графе
![]() справедливо соотношение
справедливо соотношение
![]() .
.
Два простых графа
(без петель и кратных ребер) G1
и G2 оказываются изоморфными,
если существуют взаимно однозначное
отображение
![]() ,
такое что
,
такое что
![]() .
Таким образом, изоморфными являются
графы, которые отличаются только
нумерацией вершин и ребер. Изоморфизм
графов представляет собой отношение
эквивалентности, поскольку оно обладает
свойствами:
.
Таким образом, изоморфными являются
графы, которые отличаются только
нумерацией вершин и ребер. Изоморфизм
графов представляет собой отношение
эквивалентности, поскольку оно обладает
свойствами:
Рефлексивности -
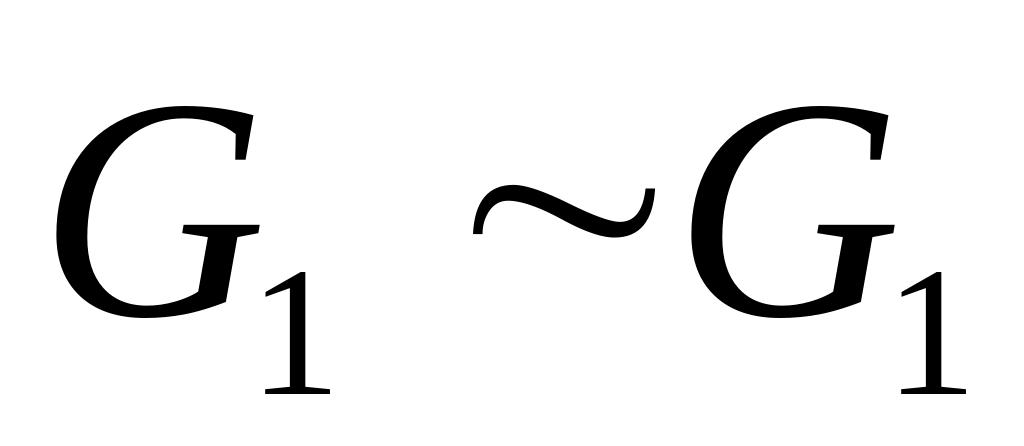 ,
причем биекция
,
причем биекция
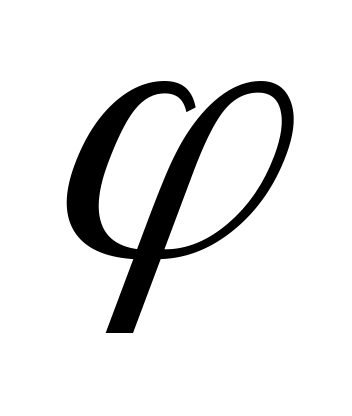 представляет собой тождественную
функцию.
представляет собой тождественную
функцию.Симметричности. Если
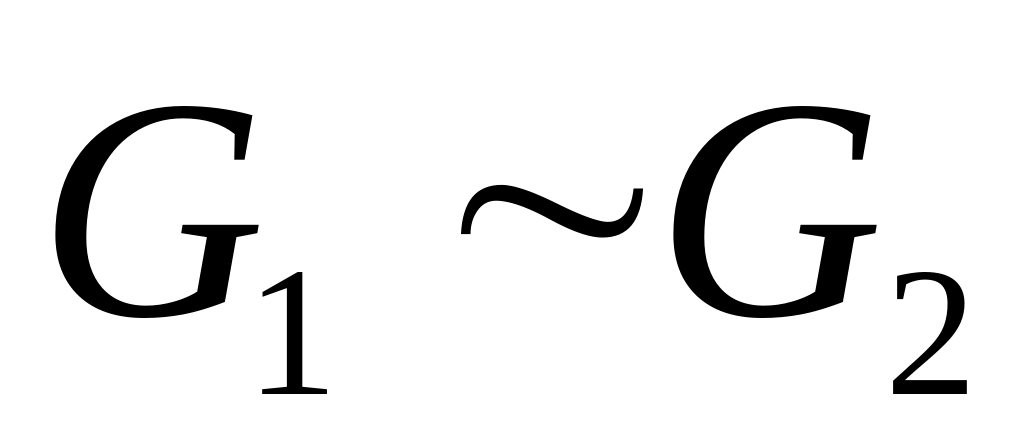 с биекцией
,
то
с биекцией
,
то
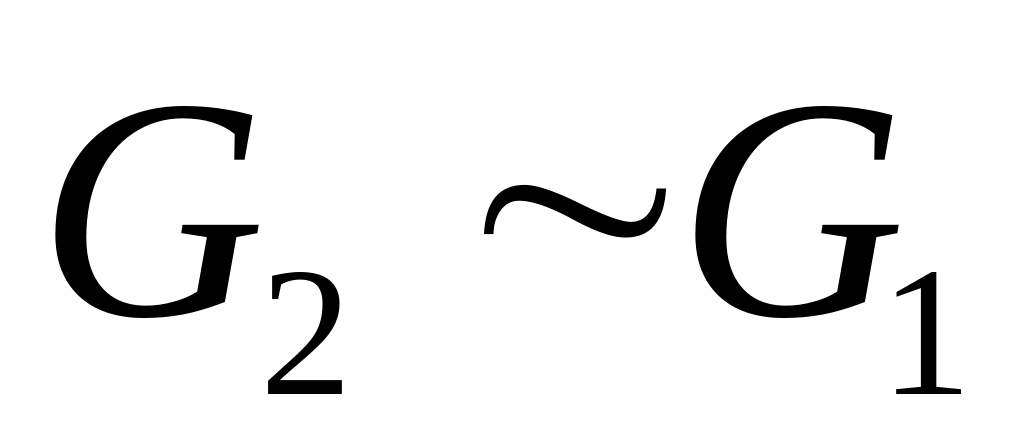 с биекцией
с биекцией
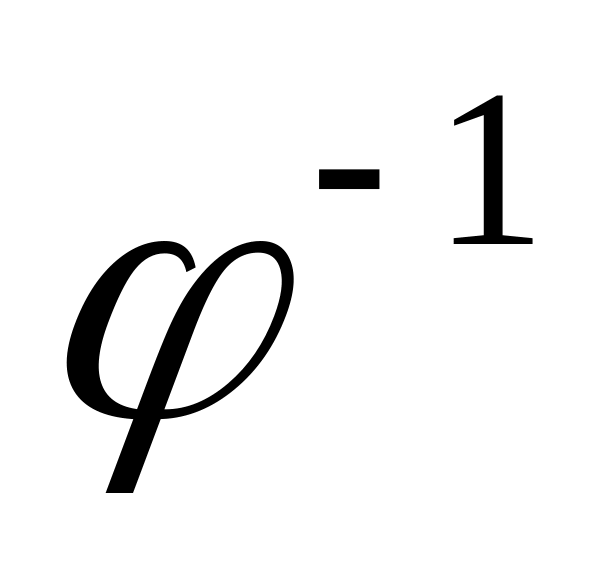 .
.Транзитивности. Если с биекцией
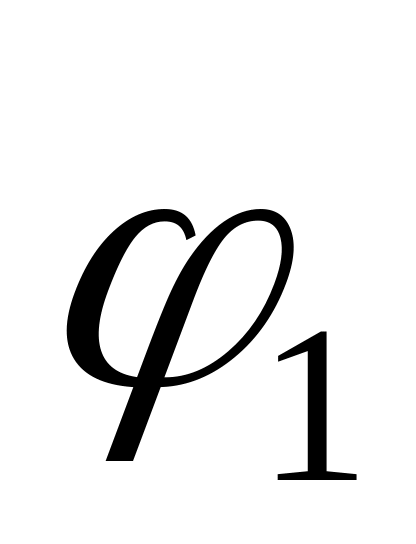 ,а
,а
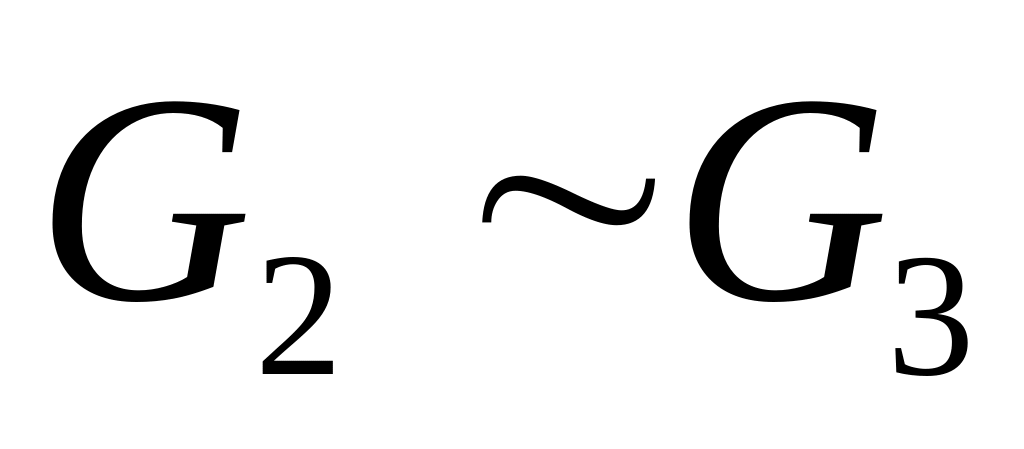 с биекцией
с биекцией
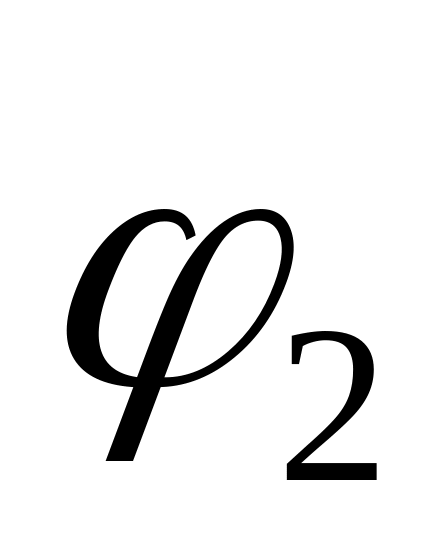 ,
то
,
то
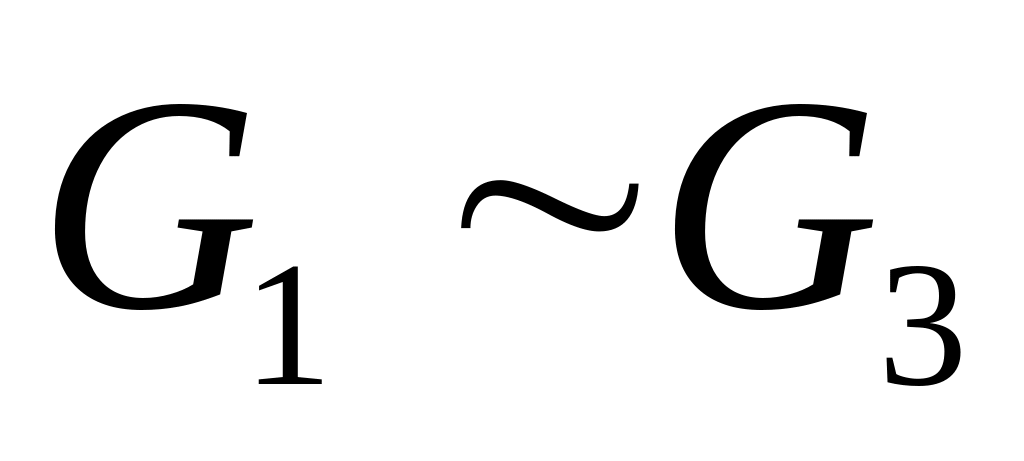 с биекцией
с биекцией
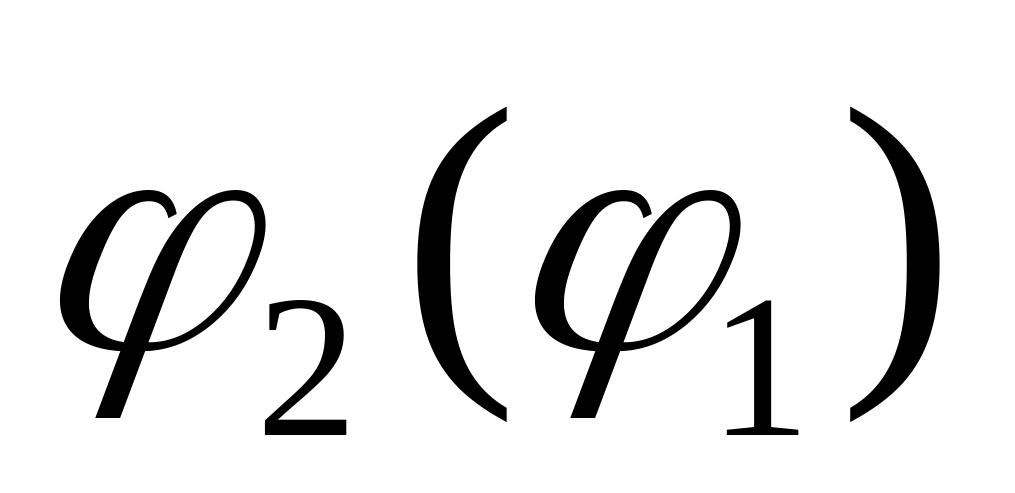 .
.
2. Представление графов в эвм и операции над ними
2.1. Матричные способы задания графов
Матрицей смежности графа G=(V,E) с n вершинами называется квадратная матрица А порядка n, элементы которой определяются следующим образом:
а) в случае неориентированного графа
![]()
б) для ориентированного графа
![]()
в)
в мультиграфе
![]() = k, где k
– кратность ребра (vi
vj).
= k, где k
– кратность ребра (vi
vj).
Пример. Для графа, изображенного на рис. 5,

Рис. 5
матрица смежности имеет вид
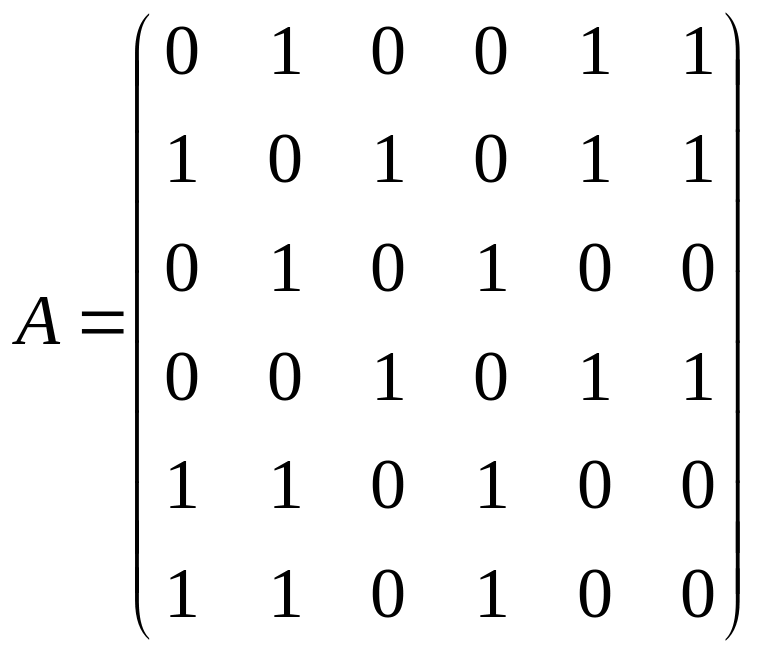
Свойства матрицы смежности: Матрица смежности неориентированного графа является симметричной относительно
главной диагонали. Диагональные элементы этой матрицы указывают на наличие петель в соответствующем графе.
Сумма элементов
матрицы А неориентированного графа
по i-ой строке (или i-му столбцу)
равна d(vi). Для
ориентированного графа сумма элементов
матрицы А по i-ой строке равна
d![]() (vi),
а по j-му столбцу d
(vi),
а по j-му столбцу d![]() (
vj).
(
vj).
Графы изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременной перестановкой строк и столбцов (i, j строк и i, j столбцов).
Объём памяти для матрицы смежности – О(n2)
Матрицей инцидентности графа G=(V, E) с n вершинами и m ребрами называется матрица В размера n×m, элементы которой определяются следующим образом:
а) для неориентированного графа
б) лля ориентированного
графа![]()
 Например,
для графа предыдущего примера:
Например,
для графа предыдущего примера:
З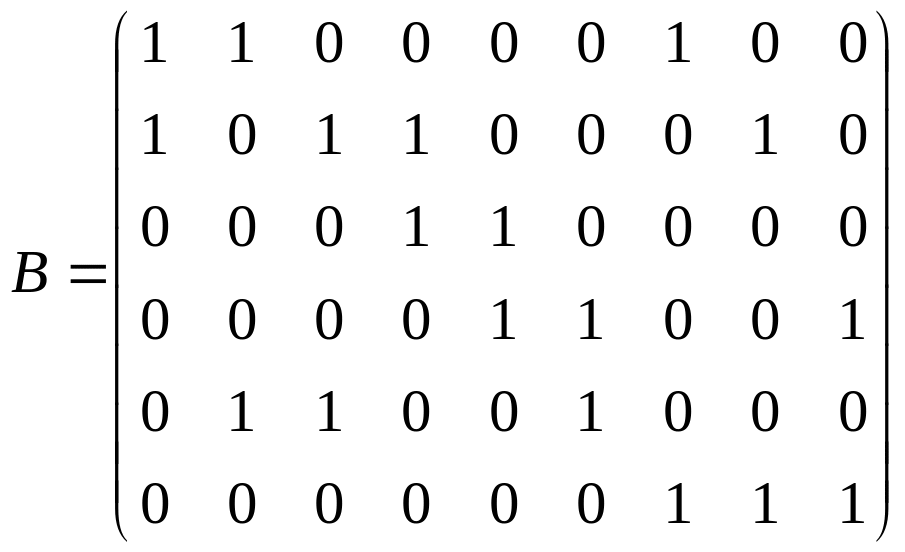 аметим,
что мультиграфы изоморфны тогда и только
тогда, когда их матрицы инцидентности
получаются друг из друга некоторыми
перестановками строк или столбцов.
аметим,
что мультиграфы изоморфны тогда и только
тогда, когда их матрицы инцидентности
получаются друг из друга некоторыми
перестановками строк или столбцов.
Объём памяти для матрицы инцидентности – О(nm)
