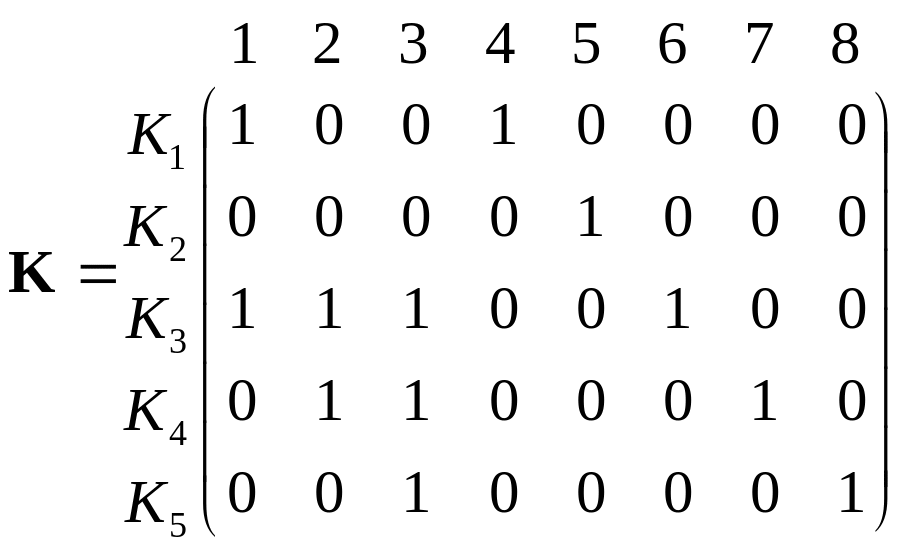- •Часть 1
- •Часть 1
- •Введение
- •1. Основные понятия теории графов
- •Задачи теории графов
- •1.2. Основные определения
- •1.3. Степени вершин графа
- •1.4. Изоморфизм графов
- •2. Представление графов в эвм и операции над ними
- •2.1. Матричные способы задания графов
- •2.2. Список ребер (луг) и структура смежности графа
- •2.3. Части графов
- •2.4. Основные операции над графами
- •3. Маршруты в графах
- •3.1. Понятие маршрута
- •Маршруты в неориентированных графах
- •Маршруты в ориентированных графах
- •3.2. Связность в графах.
- •В примере 3 граф имеет две сильно связных компоненты.
- •3.3. Связность и матрица смежности графа
- •3.4. Матрица взаимодостижимости
- •4. Деревья
- •4.1. Свободные деревья
- •4.2. Ориентированные, упорядоченные и бинарные деревья
- •Эквивалентное определение ориентированного дерева
- •5. Эйлеровы и гамильтоновы графы.
- •5.1. Эйлеровы графы.
- •5. 2. Алгоритм построения эйлерова цикла в эйлеровом графе
- •5.3. Гамильтоновы графы
- •5.4. Оценки числа эйлеровых и гамильтоновых графов
- •6. Фундаментальные циклы и разрезы
- •6.1. Фундаментальные циклы
- •6.2. Разрезы
- •7. Связь теории графов с бинарными отношениями и векторными пространствами
- •7.1. Отношения на множествах и графы
- •7.2. Векторные пространства, связанные с графами
- •8. Планарность и раскраска графов
- •8.1. Планарные графы
- •8.2. Раскраска графов
- •8.3. Алгоритм последовательной раскраски
- •9. Покрытия и независимость
- •9.1. Покрывающие множества вершин и ребер
- •9.2. Независимые множества вершин и ребер
- •9.3. Доминирующие множества
- •10. Кратчайшие маршруты в графах
- •10.1. Расстояния в графах
- •10.2. Алгоритм Форда-Беллмана
- •11. Задача коммивояжера
- •11.1. Постановка задачи
- •11.2. Обходы вершин графа по глубине и ширине
- •11.3. Решение задачи коммивояжера
- •12. Потоки в сетях
- •12.1. Основные определения
- •12.2. Теорема Форда и Фалкерсона
- •12.3. Алгоритм построения максимального потока
- •13. Сетевое планирование и управление
- •13.1. Элементы сетевого графика
- •13.2. Временные параметры сетевого графика
- •13.3. Распределение ограниченных ресурсов
- •14. Анализ технических систем (на примере электрической цепи)
- •14.1 Закон Кирхгофа
- •14.2. Основные уравнения
- •15. Сигнальные графы
- •15.1. Общие представления о сигнальных графах
- •15.2. Преобразования сигнальных графов
- •15.3. Формула Мэзона
- •16. Переключательные сети (схемы)
- •17. Математические машины и цепи маркова
- •Библиографический список
- •Оглавление
- •Часть 1
- •394026 Воронеж, Московский просп., 14
6.2. Разрезы
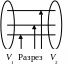 Пусть
G=(V,E)
– неорграф, V
={V1,
V2}
– разбиение множеств V.
Р
Пусть
G=(V,E)
– неорграф, V
={V1,
V2}
– разбиение множеств V.
Р азрезом
графа G
(по разбиению V)
называется множество всех ребер,
соединяющих вершины из V1
с вершинами из V2.
азрезом
графа G
(по разбиению V)
называется множество всех ребер,
соединяющих вершины из V1
с вершинами из V2.
Рис. 22
Заметим,
что в связном графе любой разрез непуст.
Непустой разрез K
неориентированного графа G
называется коциклом
(простым разрезом), если любое непустое
собственное подмножество
![]() не является разрезом. Другими словами
из К
нельзя удалить ни одно ребро с тем, чтобы
полученное множество было непустым
разрезом.
не является разрезом. Другими словами
из К
нельзя удалить ни одно ребро с тем, чтобы
полученное множество было непустым
разрезом.
Заметим, что понятие остова и коцикла является противоположными в том смысле, что остову соответствует минимальное количество ребер, которые связывают посредствам маршрутов все вершины связного графа, а коцикл состоит из минимального количества ребер, отделяющих некоторые вершины связного графа от остальных вершин.
Теорема 1. В конечном неорграфе G=(V, E), имеющим c компонент связности, множество ребер К тогда и только тогда является коциклом, когда граф (V, E\K) имеет c+1 компонент связности.
Теорема 2. В связном неорграфе остовное дерево имеет по крайней мере одно общее ребро с любым из разрезов графа.
Теорема 3. В связном неорграфе любой цикл имеет с любым разрезом четное число общих ребер.
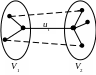 Рассмотрим
неорграф G=(V,
E)
имеющий n
вершин, m
ребер и c
компонент связности. Пусть Т
– остов графа G
и u1,
u2,
…, un-c
– множество ветвей остова Т.
Удаляя из остова Т
произвольную ветвь ui,
получим лес с (c+1)
компонентами
Рассмотрим
неорграф G=(V,
E)
имеющий n
вершин, m
ребер и c
компонент связности. Пусть Т
– остов графа G
и u1,
u2,
…, un-c
– множество ветвей остова Т.
Удаляя из остова Т
произвольную ветвь ui,
получим лес с (c+1)
компонентами
Рис. 23
связности, т.е. ребро ui является разрезом остова Т по некоторому разбиению {V1, V2}.
В
графе G
могут существовать ещё какие-то ребра
vi1,
vi2,
…, vij,
являющимися хордами остова Т
соединяющими вершины из V1
с вершинами из V2.
Множество рёбер Кi={ui,
vi1,
vi2,
…, vij}
образует простой разрез графа. Он
называется фундаментальным
разрезом
графа G,
относительно ветви ui
остова Т.
Множество {K1,
K2…,Kn-c}
всех фундаментальных разрезов графа
G,
относительно остова T,
называется фундаментальным
множеством коциклов
графа G,
относительно остова Т.
Мощность этого множества не зависит от
выбора остова Т
и равна n-c.
Число
![]() называется корангом.
называется корангом.
Фундаментальному разрезу Ki ставиться в соответствие
вектор
![]() ,
компоненты которого определяются по
правилу:
,
компоненты которого определяются по
правилу:
![]()
Фундаментальное
множество коциклов задается матрицей
фундаментальных разрезов,
строки которой являются векторами
![]() .
.
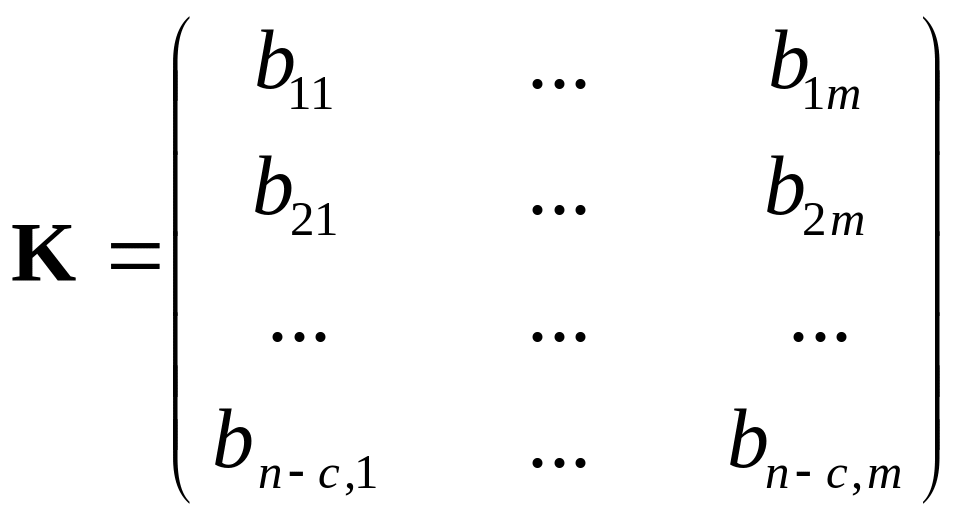
 .
.
Так как, каждый фундаментальный разрез Ki содержит ровно одну ветвь, а именно ui, то матрица К имеет следующий вид:
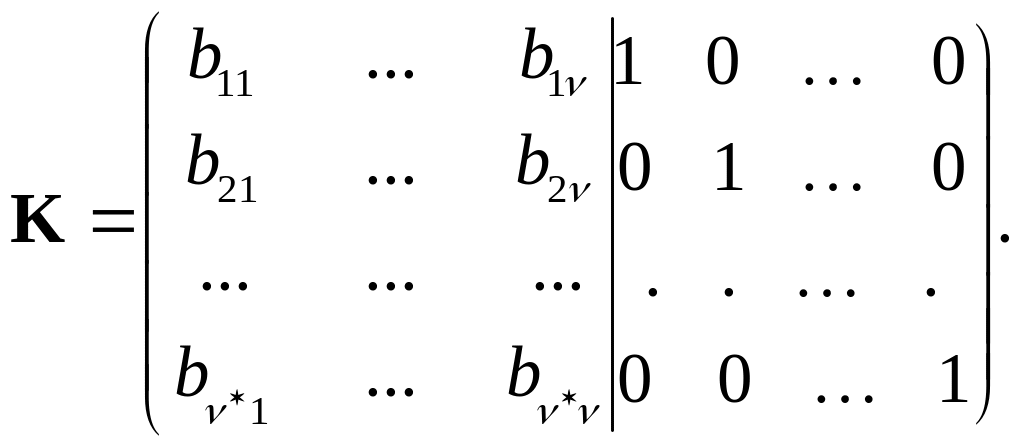
Таким
образом, матрицу К
можно представить в виде
![]() ,
где К2
– единичная матрица порядка n-c.
Заметим, что если
соответствует матрица фундаментальных
циклов, то
,
где К2
– единичная матрица порядка n-c.
Заметим, что если
соответствует матрица фундаментальных
циклов, то
![]() .
.
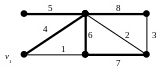 Пример:
Найти матрицу фундаментальных разрезов
графа G
изображенного на рисунке:
Пример:
Найти матрицу фундаментальных разрезов
графа G
изображенного на рисунке:
Рис. 24
Так
как, коранг
![]() то, следовательно, в данном графе имеется
пять фундаментальных разрезов (коциклов).
Ребро 4 соответствует коциклу К1={1,
4}, поскольку при удалении ребра 4 из
остова Т
множество вершин V
разбивается на две части {v1}
и V\{v1}.
А на разбиении {{v1},
{V\{v1}}}
рёбра 1 и 4 образуют разрез.
Аналогично ребру 5 соответствует коцикл
К2={5},
ребру 6 соответствует коцикл K3={1,
2, 3, 6}, ребру 7 соответствует коцикл K4={2,
3, 7} и ребру 8 соответствует коцикл K5={3,
8}. Таким образом, матрица фундаментальных
разрезов имеет вид:
то, следовательно, в данном графе имеется
пять фундаментальных разрезов (коциклов).
Ребро 4 соответствует коциклу К1={1,
4}, поскольку при удалении ребра 4 из
остова Т
множество вершин V
разбивается на две части {v1}
и V\{v1}.
А на разбиении {{v1},
{V\{v1}}}
рёбра 1 и 4 образуют разрез.
Аналогично ребру 5 соответствует коцикл
К2={5},
ребру 6 соответствует коцикл K3={1,
2, 3, 6}, ребру 7 соответствует коцикл K4={2,
3, 7} и ребру 8 соответствует коцикл K5={3,
8}. Таким образом, матрица фундаментальных
разрезов имеет вид: