
Методическое пособие 699
.pdf
через рассматриваемый элемент поверхности ребра она будет равна q sin (рис. 2.17). При этом должно быть справедливо соотношение
q sin |
t |
t ж |
, |
|
|||
или |
|
|
|
|
|
||
q sin |
|
x t1 |
t ж . |
(2.100) |
|||
h |
|||||||
|
|
|
|
|
|
||
Из равенства (2. 100) следует, что угол |
является функ- |
||||||
цией только x: |
|
|
|
|
|
||
sin |
|
|
1 |
x . |
(2.100 ) |
||
|
qh |
||||||
|
|
|
|
|
|||
Контур ребра, найденный указанным методом представ-
ляет собою дугу окружности с радиусом r, |
так как sin = x/r. |
Из уравнений (2.100 ) следует, что r = qh/ |
1. Доказано, что |
такой профиль ребра, образованный дугами окружности, обладает минимальной массой. Такое ребро и ребро треугольного сечения по массе отличаются очень мало. По технологическим причинам проще изготовить ребра треугольного профиля, поэтому на практике они используются чаще, чем ребра, образованные дугой окружности.
Ребро треугольного и трапециевидного сечения. В практике нашли широкое применение прямые ребра как треугольного сечения с острой вершиной, так и с усеченной вершиной
– трапециевидные.
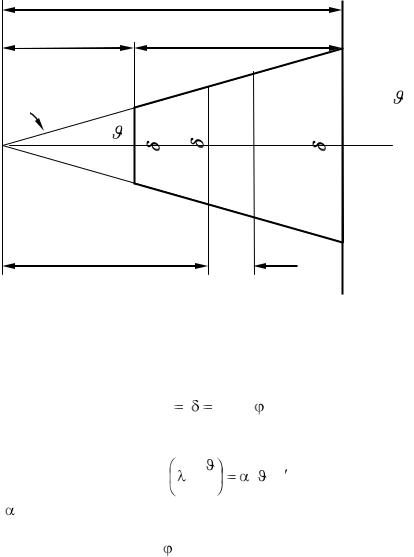
Пусть заданы размеры трапециевидного ребра (рис. 2.18) и избыточная температура 1 у его основания. За начало координат целесообразно принять вершину треугольника, направив ось x вдоль оси симметрии ребра. При этом вектор плотности теплового потока q будет направлен в сторону, противоположную положительному направлению оси x [Л. 124].
198
x2
2
2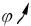
x
x1
h
1
2 |
1 |
dx
Рис. 2.18 Перенос теплоты через ребро трапециевидного сечения
Для такого ребра площадь поперечного сечения будет
функцией только координаты x: |
|
|
|||
f |
l |
2lx tg . |
(а) |
||
Количество теплоты, которое будет отдаваться в окру- |
|||||
жающую среду с элемента ребра dx, будет равно: |
|
||||
d |
f |
d |
u dx , |
(б) |
|
dx |
|||||
|
|
|
|
||
где . коэффициент теплоотдачи на поверхности ребра; u . периметр сечения ребра на расстоянии х, который можно выра-
зить как u = 2l; dx = dх/сos .
= dх/сos .
Произведя дифференцирование выражения (б) с учетом соотношения (а), получим:
198
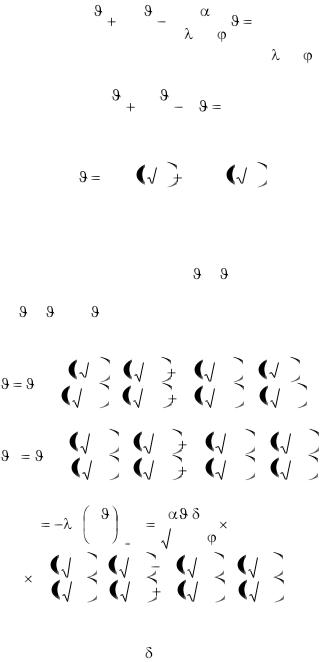
d 2 |
|
1 d |
1 |
|
|
0 . |
(в) |
|||
dx 2 |
|
|
|
|
|
|
|
|
||
|
x dx |
|
x |
|
sin |
|
||||
После введения новой переменной z = ( sin ) уравнение (в) приобретает вид:
sin ) уравнение (в) приобретает вид:
d2 |
|
1 d |
1 |
0 . |
(2.101) |
|||
|
|
|
|
|
|
|
||
dz 2 |
|
z dz |
|
z |
||||
|
|
|
|
|||||
Дифференциальное уравнение (2.101) есть модифицированное уравнение Бесселя, решение которого имеет вид:
|
|
|
|
|
|
C1I0 2 z C2 K 0 2 z , |
(2.102) |
||||
где I0 и K0 — модифицированные функции Бесселя первого и второго рода.
Постоянные С1 и С2 в уравнении (2.102) находятся из граничных условий, которые для рассматриваемого случая за-
пишутся так: при х = х1 имеет место |
= |
1. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Если пренебречь потерями тепла с торца ребра, то при х |
|||||||||||||||||||||||||||||
= х2 имеем |
= 1 и (d /dx)x=x2 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
После определения постоянных С1 |
и С2 получим: |
|
|||||||||||||||||||||||||||
для текущей температуры в ребре |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 2 z K1 2 z1 |
I1 |
2 z 2 K 0 2 z |
(2.103) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 I0 2 z1 K1 2 z 2 |
I1 2 z 2 K 0 2 z1 |
|||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
для температуры на конце ребра |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
I0 2 z 2 K1 2 z 2 |
|
I1 2 z 2 K 0 2 z 2 |
(2.104) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 I0 2 z1 K1 2 z 2 |
|
I1 2 z 2 K 0 2 z1 |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
Тепловой поток можно определить по закону Фурье:
Q |
|
|
f1 |
d |
|
|
1 1l |
|
|||||||||||||||
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x x1 |
|
z1 sin |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(2.105) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
I1 2 z1 K1 2 z2 |
I1 2 z2 K0 2 z1 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0 2 z1 K1 2 z2 |
I1 2 z2 K0 2 z1 |
|
||||||||||||||||||||
При пользовании этими формулами теплоотдача с торца может быть учтена условным увеличением высоты ребра h на половину толщины его торца 2/2.
198

Если ребро имеет треугольное сечение, то в этом случае x2 = 0, а следовательно, и z2 = 0, I1(0) = 0 и формулы (2.103) . (2.105) принимают вид:
|
I0 2 |
z |
|
; |
(2.106) |
|
1 I0 2 |
|
|
||||
z1 |
||||||
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
; |
|
|
|
(2.107) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
1 I0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 z1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Q |
1 |
|
1l |
|
I1 |
2 |
|
z1 |
|
. |
(2.108) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
z1 sin |
|
I0 |
2 |
|
z1 |
|||||||||
|
|
|
|
|
|
|
|
|||||||||
Максимальный тепловой поток через ребро треугольного сечения данной массы будет иметь место при выполнении равенства
h |
1,309 |
2 |
. |
(2.109) |
|
|
|
||||
|
3 |
|
|
|
|
1 / 2 |
|
1 |
|
|
|
|
|
|
|
||
Формулы (2.103), (2.104) и (2.105) громоздки и неудобны для практических расчетов. Поэтому расчет ребер переменного сечения можно свести к методике расчета прямых ребер постоянного сечения.
В этом случае
Q

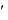 F
F q , (2.110)
q , (2.110)
где Q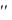 - количество передаваемой теплоты в единицу времени; F
- количество передаваемой теплоты в единицу времени; F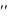 — поверхность охлаждения ребра; q = Q/F — плотность теплового потока для прямоугольного ребра, длина, высота и толщина которого равны длине, высоте толщине суженного ребра;
— поверхность охлаждения ребра; q = Q/F — плотность теплового потока для прямоугольного ребра, длина, высота и толщина которого равны длине, высоте толщине суженного ребра; 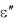 f 2 / 1 , 2 / 1 — поправочный коэффициент на
f 2 / 1 , 2 / 1 — поправочный коэффициент на
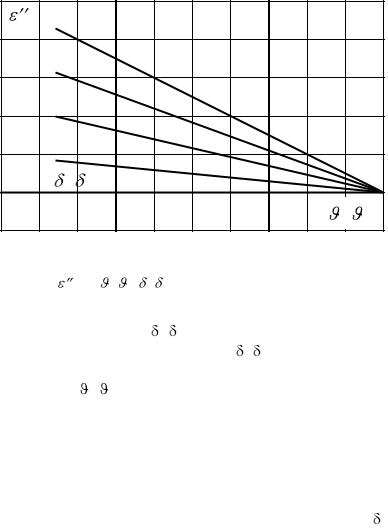
суженность ребра; 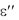 определяется по графику рис. 2.19.
определяется по графику рис. 2.19.
198
1,2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,25 |
|
|
|
|
1,1 |
|
0,50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,75 |
|
|
|
|
1,0 |
2/ 1 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2/ |
1 |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
|
Рис. 2.19 |
= f ( |
2/ 1, 2/ |
1) – вспомогательный график для |
|||
расчета ребра трапециевидного и треугольного сечений |
|
|||||
Нижняя кривая (при 2/ 1 = 1) соответствует прямому ребру постоянного сечения, а верхняя ( 2/ 1 = 0) — треугольному ребру.
Отношение 2/ 1 = 1 вычисляется по формуле (2.84). Теплоотдача с торца ребра при этом учитывается путем увеличения высоты ребра h на половину толщины торца.
2.11 Теплопроводность плоской полуограниченной однородной пластины
Рассмотрим плоскую однородную пластину шириной с постоянным коэффициентом теплопроводности и неограниченным размером в направлении оси Oy (рис. 2.20) [Л. 204].
198

y |
t1 |
|
t1 |
t1 |
|
x
0 |
t = f (x) |
Рис. 2.20 Полуограниченная пластина
Предполагается, что на поверхностях пластины, определяемых координатами х = 0, х = 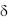 и y
и y 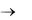 температура поддерживается постоянной и равной t1, а вдоль поверхности у = 0 температура является функцией координаты х, т. е. t = f(x). Предполагается, что пластина относительно тонкая в направлении оси Ох, а поверхности, параллельные координатной плоскости хОу, имеют идеальную тепловую изоляцию. Ввиду этого градиентом температур t/ z можно пренебречь, и температурное поле такой пластины будет двухмерным.
температура поддерживается постоянной и равной t1, а вдоль поверхности у = 0 температура является функцией координаты х, т. е. t = f(x). Предполагается, что пластина относительно тонкая в направлении оси Ох, а поверхности, параллельные координатной плоскости хОу, имеют идеальную тепловую изоляцию. Ввиду этого градиентом температур t/ z можно пренебречь, и температурное поле такой пластины будет двухмерным.
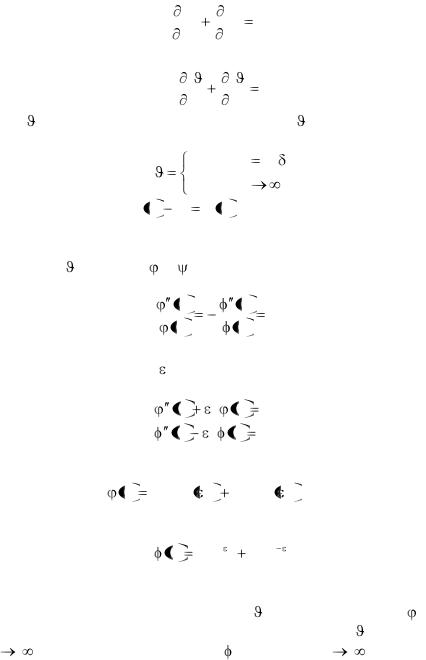
Для двухмерной стационарной задачи без внутренних источников теплоты дифференциальное уравнение теплопроводности запишется:
198
|
|
|
|
|
2 t |
|
|
|
|
2 t |
|
0 |
|
|
||||
|
|
|
|
x 2 |
|
|
|
y2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
(2.111) |
|
|
|
|
|
|
x 2 |
|
|
|
|
y2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где . температура, отсчитанная от t1, т. е. |
= t – t1. |
|||||||||||||||||
Граничные условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
при x |
0, ; |
|
(2.112) |
||||||||
|
|
|
|
|
0 |
|
при y |
; |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
f x |
|
t1 |
F x |
при y = 0. |
|
|
|||||||||||
Для решения уравнения в частных производных (2.111) |
||||||||||||||||||
воспользуемся методом разделения переменных. Предполо- |
||||||||||||||||||
жим, что |
= f(x, y) = |
(x) |
(y). Тогда уравнение (2.111) приво- |
|||||||||||||||
дится к виду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
y |
|
const |
. |
(2.113) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
x |
|
|
|
|
|
|
|
y |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Правая и левая части уравнения одинаковы и постоянны. |
||||||||||||||||||
Обозначим |
их через |
2. |
|
Таким |
образом, |
мы |
получаем два |
|||||||||||
обыкновенных дифференциальных уравнения: |
|
|||||||||||||||||
|
|
|
x |
|
|
|
2 |
|
|
x |
0 ; |
|
(2.114) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
y |
|
|
|
2 |
|
|
y |
0 . |
|
(2.115) |
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Решением дифференциального уравнения (2.114) являет- |
||||||||||||||||||
ся функция вида: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x C1 cos |
x |
C2 sin x . |
|
(2.116) |
|||||||||||||
Согласно (2.79) общее решение уравнения (2.115) будет |
||||||||||||||||||
иметь вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
C 2 e y |
C 4 e y . |
|
(2.117) |
|||||||||||
Общее решение уравнения (2.111) получим после перемножения уравнений (2.116) и (2.117). Решение (2.116) будет удовлетворять граничному условию = 0 при х = 0, когда (х)
= 0 при х = 0, а это возможно при С1 = 0. Условие |
= 0 при y |
выполняется тогда, когда (y) = 0 при y |
что воз- |
198

можно лишь при С3 = 0. Таким образом, решение для (2.111) приводится к виду
Ce y sin |
x . |
Для того чтобы полученное выражение удовлетворяло |
|
граничным условиям = 0 при х = |
должно быть sin ( ) = 0 |
или = n / (где n = 1, 2, 3 ...). |
|
Каждому значению n соответствует частное решение, а каждому частному решению соответствует свое значение постоянной интегрирования. Общее решение есть сумма частных решений для всех последовательных положительных значений чисел n:
n |
n |
y sin |
n |
|
|
|
|
|
|||
Cn e |
|
x . |
(2.118) |
||
|
|
||||
n 1 |
|
|
|
|
|
Полученное решение удовлетворяет и третьему граничному условию, т. е. = 0 при y 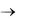 .
.
Оставшиеся постоянные Сn определяются из граничных условий = F(х) при у = О. При этом
|
n |
n |
|
|
F x |
Cn sin |
x . |
||
|
||||
|
n 1 |
|
|
Это равенство есть разложение функции F(х) в ряд Фурье по синусам. Коэффициенты ряда Фурье определяются следующим выражением:
Cn |
2 |
F x sin |
n |
x dx . |
|
|
0
Окончательное решение для температурного поля рассматриваемой задачи с учетом последнего соотношения можно записать в виде
2 n |
Cn sin |
n |
x F x sin |
n |
x dx . |
(2.119) |
|
|
n 1 |
|
|
||||
|
|
|
0 |
|
|
|
|
Итак, окончательное решение рассмотренной двухмерной задачи после определения постоянных интегрирования представится суммой бесконечного ряда.
Аналогичным образом можно пол решение и для сплош-
198
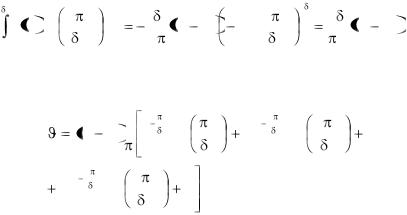
ного цилиндра при изменении температурного поля в двух измерениях. Окончательное решение, как и для пластины, представится суммой бесконечного ряда.
При решении конкретной задачи вычисляют интеграл в уравнении (2.119), исходя из условий задания температуры. Следующим
этапом является вычисление членов ряда в зависимости от условий сходимости в требуемой точности вычислений.
Например, если t = t2 = const при y = 0, то f(х) = t2, а F(х) =t2 – t1. Интеграл
F x sin |
n |
x dx |
|
t 2 t1 |
cos |
n |
x |
2 |
|
t |
2 t1 , |
|
|
n |
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
0 |
|
n |
|
||
|
|
|
|
|
|
|
|
|
|
|
||
(n = 1, 3, 5, 7, …).
Подставим этот интеграл в уравнение (2.119), получим:
|
|
|
|
|
4 |
|
|
|
|
y sin |
|
x |
1 |
e |
3 |
y sin |
3 |
|
|
|
t2 |
t1 |
|
e |
|
|
|
x |
|||||||||
|
|
|
|
|
3 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.120) |
|
1 |
|
y sin |
|
5 |
|
|
|
|
|
|
|
|||||||
e |
|
|
|
x ... . |
|
|
|
|
|
|
||||||||
5 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Можно показать, что полученный ряд сходится. Для вычисления изотерм существуют различные методы. Наиболее точным является метод, при котором y принимается в качестве постоянного параметра. По серии кривых, отвечающих постоянному значению у, строят изотермы.
2.12 Пористое охлаждение пластины
Пористые материалы находят большое применение в таких конструкциях, как высокотемпературные теплообменники, турбинные лопатки, реактивные сопла и т. д. На практике охлаждение пористых структур достигается нагнетанием жидкости или газа через капилляры твердого тела. Процесс теплообмена в таких пористых системах весьма сложен. При решении
198
задачи предполагается, что вся передача теплоты внутри плоской пластины осуществляется за счет теплопроводности через твердую фазу, и что температуры твердого тела и жидкости почти не отличаются друг от друга в любой точке пористой структуры. Эти предположения существенно упрощают решение задачи.
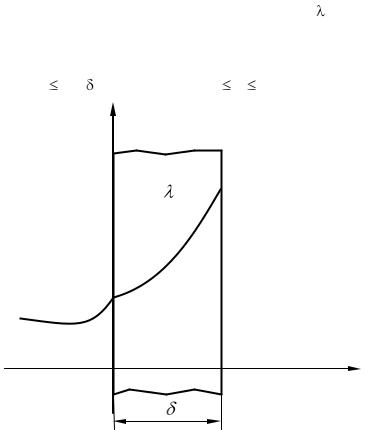
Рассмотрим показанную на рис. 2.21 плоскую пластину с постоянным коэффициентом теплопроводности с. Размеры пластины в направлениях y и z велики и температурное поле внутри пластины можно считать одномерным; последнее справедливо и для температуры охлаждающей жидкости, т. е. t = t(х) при 0 x 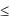 и tж = tж(x) при .
и tж = tж(x) при .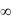 x 0.
x 0.
t
c tc2
tc1
tж0
x
Жидкость или газ
Рис. 221 Пористое охлаждение плоской пластины
На поверхности пластины при х = 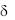 температура стенки равна tc2. Температура нагнетаемой вдоль оси Ох через пла-
температура стенки равна tc2. Температура нагнетаемой вдоль оси Ох через пла-
198
