
Методическое пособие 699
.pdf
тела конечных размеров свелось к решению задачи для безграничной пластины конечной толщины. Уравнение (3.81) можно представить в виде:
F |
|
x |
, |
x |
, |
a |
F |
|
y |
, |
y |
, |
a |
|
|
F |
z |
, |
|
z |
, |
a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
|
|
2 |
y |
|
|
|
|
|
|
2 |
|
z |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
x |
|
|
y |
y |
|
z |
|
|
|
|
z |
|
||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fx |
X, Bi x , Fo x |
Fy |
Y, Bi y , Fo y |
Fz |
Z, Bi z , Fo z |
. |
|
(3.81 ) |
|||||||||||||||
Множители в уравнении (3.81) вычисляются по формуле
(3.24).
Рассмотренный метод известен в теории теплопроводности под названием теоремы о перемножении решений. Полученное решение справедливо и для нахождения средней температуры.
Средняя безразмерная температура параллелепипеда выражается следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
y t ж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t |
ж |
|
|
|
t |
x |
t |
ж |
t |
|
|
z |
t |
ж |
, |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t 0 |
|
t ж |
|
|
|
|
|
|
t 0 |
t ж |
|
|
|
|
|
|
t 0 |
t ж |
t 0 |
|
t ж |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Biz , Foz . (3.82) |
|||||||||||||||||||||
|
|
|
|
|
|
x y |
|
z |
|
Fx Bi x , Fox |
Fy Bi y , Foy |
Fz |
|||||||||||||||||||||||||||
В уравнении (3.82) множители находятся по формуле (3.39). Заметим, что теорема о перемножении решений справедлива и в более общем случае, когда коэффициенты теплопроводности различны для различных направлений, коэффициенты теплоотдачи на гранях разные.
б) Охлаждение длинного прямоугольного стержня
Однородный стержень охлаждается в среде с постоянной температурой tж и при постоянном коэффициенте теплоотдачи на его поверхности. В начальный момент времени (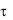 = 0) все точки стержня имеют одинаковую температуру.
= 0) все точки стержня имеют одинаковую температуру.
Поперечное сечение стержня представляет собой прямоугольник размерами 2 x 2 y (рис. 3.17). Такое тело можно рас сматривать как результат пересечения двух пластин толщиной
198
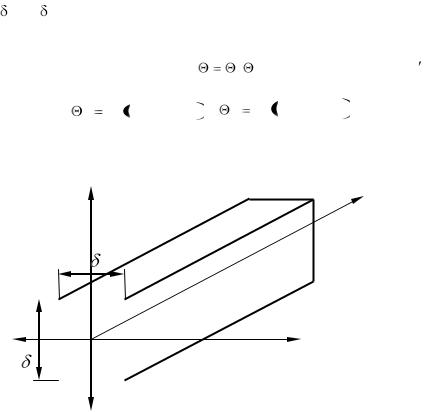
2 x и 2 y, условия однозначности для которых такие же, как и для образовавшегося стержня. Безразмерное температурное поле для поставленной задачи есть
x |
y , |
(3.82 ) |
где |
|
|
x Fx X, Bi x , Fox и y |
Fx Y, Bi y , Fo z . |
|
Множители в уравнении (3.82) вычисляются по формуле
(3.24).
y
z
2 x
- x |
|
|
|
2 |
y |
0 |
|
|
|||
|
|
|
|
- y
Рис. 3.17 К охлаждению полуограниченного прямоугольного стержня
в) Охлаждение цилиндра конечной длины
198
z
-
-
|
|
y |
z |
|
|
0 |
r |
x |
|
|
|
|
|
z |
|
|
2 |
z |
|
|
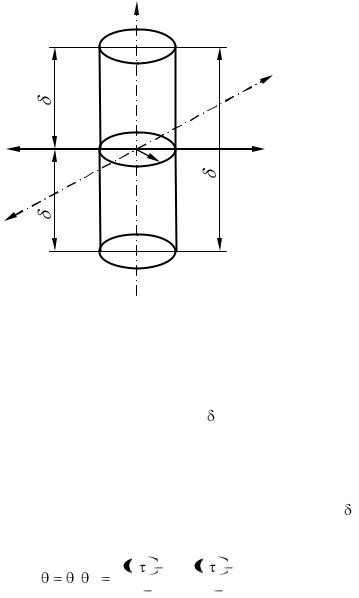
Рис. 3.18 К охлаждению цилиндра конечной длины
Однородный цилиндр охлаждается в среде с постоянной температурой tж. Коэффициент теплоотдачи с на основаниях цилиндра и его поверхности одинаков. В начальный момент ( = 0) все точки цилиндра имеют одинаковую температуру t0. Диаметр цилиндра равен 2r0, длина l = 2 z (рис. 3.18). Необходимо найти распределение температуры в цилиндре для любого момента времени и среднюю температуру как функцию времени для заданных условий однозначности. Конечный цилиндр можно рассматривать как результат пересечения безграничных цилиндра диаметром 2r0 и пластины толщиной 2 z; следовательно, и безразмерную температуру для такого тела можно записать как
= 0) все точки цилиндра имеют одинаковую температуру t0. Диаметр цилиндра равен 2r0, длина l = 2 z (рис. 3.18). Необходимо найти распределение температуры в цилиндре для любого момента времени и среднюю температуру как функцию времени для заданных условий однозначности. Конечный цилиндр можно рассматривать как результат пересечения безграничных цилиндра диаметром 2r0 и пластины толщиной 2 z; следовательно, и безразмерную температуру для такого тела можно записать как
|
t z, |
t ж |
|
t r, |
t ж |
, |
(3.83) |
z r |
|
|
|
|
|
||
t 0 |
t ж |
|
t 0 |
t ж |
|
||
|
|
|
|||||
или
198
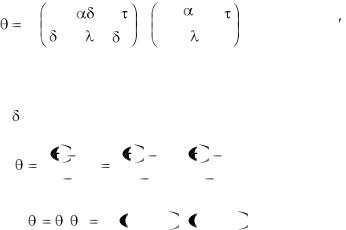
F |
z |
, |
z |
, |
a |
F |
r |
, |
r0 |
, |
a |
|
. |
(3.83 ) |
|
|
|
|
|
|
|
||||||||
z |
x |
2 |
r |
r |
|
|
|
r |
2 |
|
|
|||
|
|
|
z |
|
0 |
|
0 |
|
|
|||||
В уравнении (3.83) множители правой части находятся по формулам (3.24) и (3.53), причем в качестве определяющих линейных размеров в уравнении (3.24) берется половина высоты цилиндра z, а в уравнении (3.53) . радиус цилиндра r0. Средняя температура в цилиндре для любого момента времени
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
t ж |
|
|
|
t |
z |
|
t ж t |
r |
t ж |
, |
|
||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
t 0 |
t ж |
|
|
|
|
|
t 0 |
t ж |
t 0 |
t ж |
|
||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bi, Fo r . |
(3.84) |
|||||||||||
|
|
|
|
|
|
|
|
|
z |
|
r |
|
Fz |
Bi z , Fo Fr |
|||||||||||||||
В уравнении (3.84) множители вычисляются по форму-
лам (3.39) и (3.65).
3.9 Зависимость процесса охлаждения (нагревания) от формы и размеров тела
Скорость процесса распространения теплоты в телах зависит от отношения поверхности тел к их объему. Исследования процессов охлаждения тел указывают на то, что чем больше отношение поверхности тела к его объему, тем и скорость протекания процесса будет больше.
198
1,0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
0,5 |
|
|
3 |
|
|
5 |
|
4 |
|
|
|
|
|
|
|
||
|
|
6 |
|
|
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
|
F0 = |
/r2 |
|
|
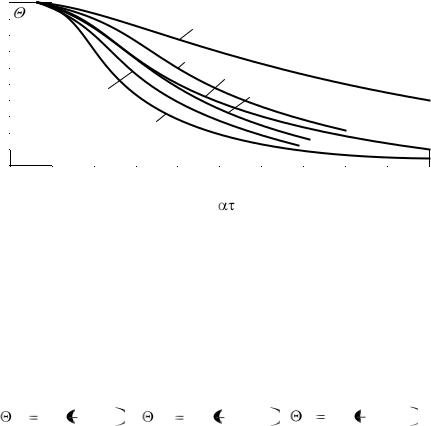
Рис. 3.19 Скорость охлаждения в центре для различных тел с одинаковым линейным диаметром l0:
1 – безграничная пластина; 2 – квадратная балка бесконечной длины; 3 – цилиндр; 4 – куб; 5 – цилиндр, длина равна диаметру; 6 – шар.
Сказанное справедливо для любых значений числа Вi и может быть наглядно продемонстрировано на примере охлаждения пластины, длинного цилиндра и шара. При Вi = 0 для пластины, цилиндра и шара уравнения температурного поля запишутся соответственно
пл |
exp |
BiFo ; |
цил |
exp 2BiFo ; |
ш |
exp 3BiFo . |
|
|
|
|
Из приведенных уравнений следует, что при одинаковом определяющем размере и прочих равных условиях наибольшая скорость изменения температуры во времени будет наблюдаться для шара. Если сравнивать отношения поверхности к объему для пластины, цилиндра и шара, то их можно представить как 1 : 2 : 3.
На рис. 3.19 приведены кривые изменения температуры во времени на оси и в центре тел различной геометрической формы при одинаковом значении числа Вi. Из рис. 3.19 следует, что для шара скорость охлаждения больше, чем для любого, другого тела. Следует помнить. что все сказанное справед-
198
ливо для тел с одинаковым характерным линейным размером l0.
3.10 Регулярный режим охлаждения (нагревания) тел
Анализ полученных решений для тел различной геометрической формы показывает, что они имеют одинаковую структуру, т. е. представляют собой сумму бесконечного ряда, члены которого расположены по быстро убывающим экспоненциальным функциям. Например, для безграничной пластины при охлаждении ее в среде с постоянной температурой tж и постоянным коэффициентом теплоотдачи 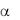 на ее поверхностях получено:
на ее поверхностях получено:
|
|
x |
|
2 |
a |
|
A n cos |
|
e |
n |
2 . |
||
|
|
|||||
n |
|
|
||||
n1
Вэтом уравнении Аn . коэффициент, свой для каждого члена ряда (не зависящий ни от координат, ни от времени), он найден из начальных условий.
Множитель cos ( nx/ ) является функцией только координаты х и его можно обозначить Un. Экспонента будет убывать пропорционально времени . Комплекс 2n / 2 представляет собой постоянное вещественное положительное число, которое можно обозначить mn, причем m будет изменяться в зависимости от номера индекса так же, как и , т. е.
m1 m 2 m3 ... m n , |
(3.85) |
где n = 1, 2, 3 …
С учетом сказанного выражение для пластины можно
представить как |
|
|
|
|
|
A |
n |
U |
n |
e mn . |
(3.86) |
|
|
|
|
||
n 1 |
|
|
|
|
|
198
ln
ln
ln |
|
I стадия |
II стадия |
x = 0
x = 1
1
180 -
2 |
|
180 |
- |
1 |
2 |
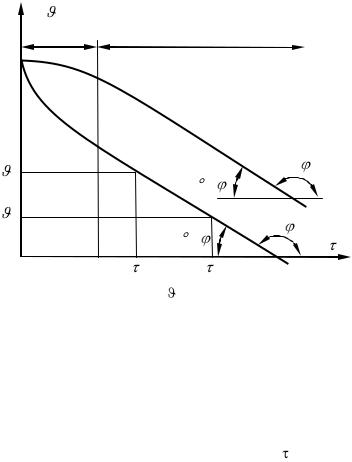
Рис. 3.20 Зависимость ln от времени при охлаждении (нагревании) тел
Для тел других геометрических форм температурное поле также будет описываться уравнением вида (3.86). Специфика геометрической формы учитывается различным видом множителей Аn и Un. Для тел одной и той же формы различным начальным распределениям температуры будут соответствовать разные совокупности чисел Аn.
При малых значениях 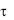 от
от 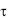 = 0 до
= 0 до 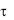 = 1 распределение температуры внутри тела и скорость изменения во времени температуры в отдельных точках тела зависят от особенностей начального распределения температур. В этих условиях поле температур в теле будет определяться не только первым, но и последующими членами ряда (3.86).
= 1 распределение температуры внутри тела и скорость изменения во времени температуры в отдельных точках тела зависят от особенностей начального распределения температур. В этих условиях поле температур в теле будет определяться не только первым, но и последующими членами ряда (3.86).
Это первый период охлаждения, при котором скорость изменения температуры внутри тела зависит от вида начального распределения температуры, называют неупорядоченной стадией процесса охлаждения (нагревания). Благодаря неравенству (3.85) с увеличением времени 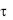 последующие члены
последующие члены
198
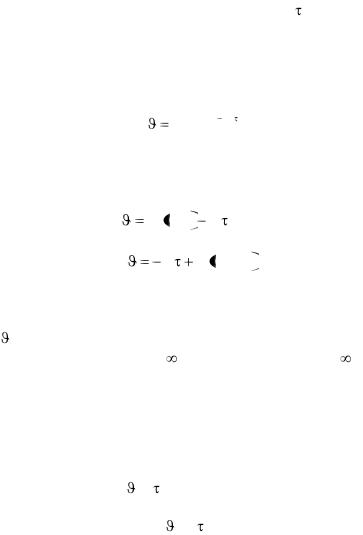
ряда (3.86) будут быстро убывать, т. е. ряд становится быстросходящимся.
Начиная с некоторого момента времени 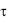 > 1 начальные условия начинают играть второстепенную роль и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формой и размерами. Температурное поле описывается первым членом ряда (3.86):
> 1 начальные условия начинают играть второстепенную роль и процесс полностью определяется только условиями охлаждения на границе тела и среды, физическими свойствами тела и его геометрической формой и размерами. Температурное поле описывается первым членом ряда (3.86):
m1 . (3.87)
Это соотношение показывает, что изменение избыточной температуры как в пространстве, так и во времени не зависит от начального распределения температуры. Логарифмируя по-
следнее уравнение и опуская индексы, получаем: |
|
||
ln |
ln AU |
m |
|
или |
|
|
|
ln |
m |
C x, y, z . |
(3.88) |
Из уравнения (3.88) следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линей ному закону. Графическая зависимость между ln и временем будет иметь вид прямой (рис. 3.20). При длительном охлаждении (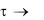 или, что то же, F0
или, что то же, F0 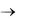 ) все точки тела в конце концов принимают одинаковую температуру, равную tж (наступило стационарное со стояние).
) все точки тела в конце концов принимают одинаковую температуру, равную tж (наступило стационарное со стояние).
Таким образом, весь процесс охлаждения можно разделить на три стадии.
Первая стадия (неупорядоченного) режима характеризуется большим влиянием начального распределения температу-
ры, и зависимость между и |
описывается уравнением (3.86). |
Вторая стадия охлаждения называется регулярным ре- |
|
жимом, и зависимость между |
и описывается уравнением |
(3.87). |
|
Третья стадия охлаждения соответствует стационарному режиму, когда температура во всех точках тела равна температуре окружающей среды (имеет место тепловое равновесие).
Остановимся на более подробном рассмотрении второй
198

стадии охлаждения.
После дифференцирования обеих частей уравнения (3.88) по времени получим:
1 |
|
|
m const . |
(3.89) |
|
|
|
||
|
|
|||
|
|
r |
|
|
В левой части уравнения (3.89) стоит выражение для относительной скорости изменения температуры, и оно равняется постоянной величине m, не зависящей ни от координат, ни от времени.
Величина m измеряется в 1/с и называется темпом охлаждения. При наступлении регулярного режима темп охлаждения не зависит ни от координат, ни от времени и является величиной постоянной для всех точек тела. Темп охлаждения, как это следует из уравнения (3.89), характеризует относительную скорость изменения температуры в теле и зависит только от физических свойств тела, процесса охлаждения на его поверхности, геометрической формы и размеров тела.
Итак, регулярный режим охлаждения (нагревания) тел характеризуется тем, что изменение температурного поля во времени, описывается простой экспонентой и относительная скорость охлаждения m для всех точек тела остается величиной, не зависящей ни от координат ни от времени.
Если экспериментально определить изменение избыточной температуры во времени и построить зависимость в полулогарифмических координатах, то из рис. 3.20 следует, что темп охлаждения в стадии регулярного режима найдется как
ln 1 |
ln 2 |
m const. |
|
2 |
1 |
||
|
Выражение для зависимости темпа охлаждения m от физических свойств тела, его геометрической формы и размеров, а также условий теплообмена на поверхности тела можно найти из анализа теплового баланса.
Изменение внутренней энергии тела
198

dQ |
c V |
v |
d , |
(3.90) |
||
|
||||||
где, с – удельная теплоемкость, Дж/(кг К); V – объем тела, м3; |
||||||
. плотность вещества, кг/м3; |
|
|
v . средняя по объему избыточ- |
|||
|
|
|||||
ная температура, С; . время, с.
С другой стороны, за тот же промежуток времени вся теплота должна быть отведена с поверхности тела в окружаю-
щую среду за счет теплоотдачи |
|
|
|
|
|
|
|
|
|
|
|
|||||
dQ |
|
|
|
|
F Fd ; |
|
|
(3.91) |
||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
||||||||||||||
Приравнивая выражения (3.90) и (3.91), находим: |
||||||||||||||||
|
|
|
v |
|
|
|
|
F |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
c V |
|
|
F |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
или, если разделить полученное выражение на |
|
v |
и учесть, |
|||||||||||||
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что c V = С, Дж/К – полная теплоемкость тела,
|
1 |
|
|
|
v |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
||
|
|
v |
|
|
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
||
CF . (3.92)
В левой части этого выражения стоит относительная скорость охлаждения m, 1/с, и если отношение F / v обозначить через , (3.92) можно записать:
m |
|
|
F |
|
|
|
|||
|
|
|
|
|
|
C |
|||
|
|
|||
Из уравнения (3.93) следует, что относительная скорость |
||||
охлаждения или, иначе говоря, темп охлаждения m однородного и изотропного тела при конечном значении коэффициента теплоотдачи пропорциональна коэффициенту теплоотдачи, поверхности тела и обратно пропорциональна его теплоемкости (первая теорема Кондратьева [Л.76]).
В уравнении (3.93) множитель 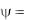
 F / v называется ко-
F / v называется ко-
эффициентом неравномерности распределения температуры в теле и зависит от условий охлаждения на поверхности тела. Для выяснения характера зависимости коэффициента 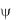 от
от
198
