
Методическое пособие 699
.pdf
числа Bi, учитывающего условия протекания процесса на поверхности, рассмотрим два предельных случая:
а) Bi 0 (практически Bi<0,1)
Как было сказано, эти условия соответствуют внешней задаче, когда распределение температуры в теле зависит от его размеров и физических свойств и, следовательно, усредненные по поверхности и объему температуры будут одинаковы:
F  v (рис. 3.8). Коэффициент неравномерности распределения температуры в теле
v (рис. 3.8). Коэффициент неравномерности распределения температуры в теле
F 1
v
б) Bi (практически Bi>100)
(практически Bi>100)
При этих условиях задача становится внутренней и процесс охлаждения определяется только размерами тела и его физическими свойствами.
В силу большой интенсивности теплообмена температура на поверхности тела принимает постоянное значение, равное температуре окружающей среды (рис. 3.7). Коэффициент неравномерности распределения температуры
F 0 .
v
198
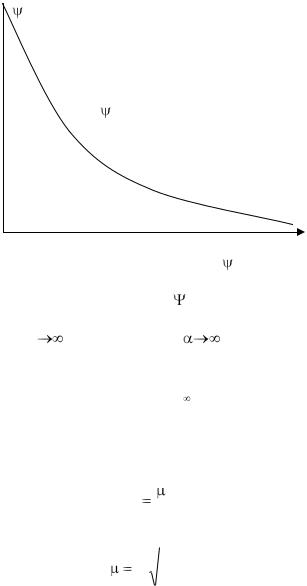
1,0
=f(Bi)
|
|
|
Bi |
0 |
|
|
|
|
Рис. 3.21 Зависимость |
= f(Bi) |
|
Из сказанного следует, что |
будет изменяться от нуля |
||
до единицы (рис. 3.21). |
|
|
|
При Bi |
или, что то же, |
, |
темп охлаждения m |
становится прямо пропорциональным коэффициенту температуропроводности тела a, м2/с (вторая теорема Кондратьева):
a = Km . |
(3.94) |
Коэффициент пропорциональности К зависит только от геометрической формы и размеров тела. Докажем это на примере охлаждения однородной безграничной пластины. Напомним, что
m |
|
2a |
|
, |
||
|
l2 |
|||||
|
0 |
|
|
|
|
|
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
l0 |
|
m |
. |
(3.95) |
||
|
|
|||||
|
|
a |
|
|||
Рассмотрим характеристическое уравнение для безграничной пластины
198

|
ctg |
|
. |
|
|
Bi |
|
||
При Bi |
имеем ctg 0, |
а стремится к своему пре- |
||
дельному значению /2; при Bi |
0 ctg |
и устремится к |
||
нулю. |
|
|
|
|
Следовательно, величина |
для пластины во всем диа- |
|||
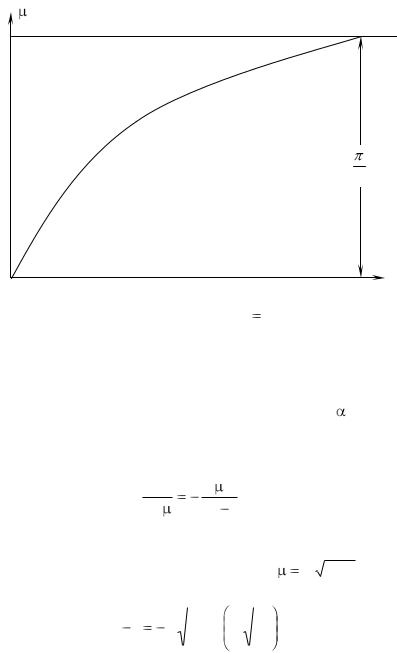
пазоне значений чисел Bi изменяется от нуля до своего предельного значения, равного /2 (рис. 3.22). Для тел другой геометрической формы имеют место свои изменения величины .
Так как при Bi (практически Bi>100) при охлаждении бесконечной пластины можно принять = /2, то из уравнения (3.95) получаем:
(практически Bi>100) при охлаждении бесконечной пластины можно принять = /2, то из уравнения (3.95) получаем:
|
|
2 |
|
||
m |
|
|
a . |
(3.96) |
|
2l |
0 |
||||
|
|
|
|||
Напомним, что для пластины характерным линейным |
|||||
размером является половина ее толщины, т.е. l0 = |
. Тогда из |
||||
уравнения (3.96) получаем:
|
|
|
a |
|
1 |
|
m |
Km , |
|
|
|
|
|
||||
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
где K |
1 |
|
. коэффициент пропорциональности для без- |
|||||
|
|
|||||||
/ 2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|
граничной пластины, который определяется только формой и геометрическими размерами.
Коэффициенты пропорциональности для тел других геометрических форм [Л. 76]:
для шара:
1
K 2 ;
r0
для параллелепипеда:
198

K |
|
|
|
1 |
|
|
; |
|
|
|
|
|
|||||
|
2 |
2 |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
l1 |
l2 |
l3 |
||||
для цилиндра конечной длины:
K |
|
1 |
|
. |
|
|
|
|
|||
2,405 |
2 |
2 |
|||
|
|
||||
|
|
|
|||
|
|
|
|
r0 l
На основе теории регулярного режима разработаны различные экспериментальные методики определения теплофизических характеристик разных материалов [Л. 139, 142]. При определении физических параметров тела поступают следующим образом.
Для определения коэффициента температуропроводности используют а-калориметр, имеющий форму цилиндра или шара. Создают условия, близкие к а , измеряют изменение избыточной температуры во времени и строят зависимость в полулогарифмических координатах (рис. 3.23). Тогда
m |
ln 1 |
ln 2 |
. |
|
2 |
1 |
|||
|
|
Из уравнения а = Km находят коэффициент температуропроводности.
находят коэффициент температуропроводности.
198
2
Bi
0
Рис. 3.22 Зависимость  f1 (Bi)
f1 (Bi)
Для определения коэффициента теплопроводности выбирают ламбда-калориметр. Обычно калориметр строят в виде шара. Сущность метода заключается в том, что создают условия охлаждения, когда коэффициент теплоотдачи остается конечной величиной, и при этих условиях определяется темп охлаждения описанным выше способом. Далее из характеристического уравнения, которое для шара имеет вид
1 |
Bi 1 , |
(3.97) |
ctg |
находят коэффициент теплопроводности.
Напомним, что для шара характерным линейным раз-
мером является его радиус r0; |
величина |
|
r0 m / a . Тогда |
||||||
уравнение (3.97) принимает вид: |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Bi 1 |
r |
|
m |
ctg r |
m |
; |
|||
|
|
|
|||||||
|
0 |
|
a |
0 |
|
a |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
198 |
|
|
|
|
|||

тогда
|
|
|
|
|
|
|
r0 |
|
|
|
; |
(3.98) |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
1 r |
m |
ctg r |
m |
|
|||||||||
|
|
|
|
|
|
||||||||
0 |
|
a |
0 |
|
a |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
здесь измеряется в Вт/(м К). |
|
|
|
|
|
|
|
|
|
|
|
||
В уравнении (3.98) неизвестная величина |
определяет- |
||||||||||||
ся на эталонном калориметре, изготовленном из материала с известным коэффициентом теплопроводности.
Мы рассмотрели метод регулярного теплового режима для условий, когда температура среды постоянна (tж = const) и который Г.М. Кондратьев назвал регулярным режимом первого рода.
В последние годы получили развитие и широкое распространение методы регулярного режима для случаев, когда
температура среды – линейная функция времени t ж |
t ж 0 b |
||
и |
температура |
среды – периодическая функция |
времени |
t ж |
t ж 0 t m cos |
(где . частота колебаний, tm – амплитуда |
|
колебания температуры среды). Эти два случая получили название методов регулярного режима второго и третьего рода.
ln
0
Рис. 3.23 К определению темпа охлаждения m
198

А.В. Лыков в монографии показал, что регуляризация кинетики нагревания тела происходит не только по температурным полям, но и по потокам теплоты. Поэтому при нагревании нет надобности различать регулярные режимы первого, второго и третьего родов. В качестве общего свойства теплового регулярного режима можно принять соотношение
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
m(t |
ж |
t) , |
(3.99) |
|||
|
|
|
|||||
d |
|
||||||
|
|
|
|
|
|
||
где t - средняя по объему тела температура; tж – температура среды; m – коэффициент пропорциональности, называемый темпом нагревания (охлаждения).
Из соотношения (3.99) следует, что скорость нагревания тела в стадии регулярного теплового режима dt/d пропорциональна разности температур среды и средней по объему тела, причем коэффициент пропорциональности m определяется не только характерными размерами тела, физическими свойствами и условиями теплообмена на поверхности, но и характером изменения температуры среды. С подобным изложением приведенного обобщенного метода можно познакомиться в указанной монографии А.В. Лыкова.
пропорциональна разности температур среды и средней по объему тела, причем коэффициент пропорциональности m определяется не только характерными размерами тела, физическими свойствами и условиями теплообмена на поверхности, но и характером изменения температуры среды. С подобным изложением приведенного обобщенного метода можно познакомиться в указанной монографии А.В. Лыкова.
Теория регулярного режима может быть применена при решении таких практических задач, как определение времени прогрева (охлаждения) тел, определение теплофизических параметров вещества, коэффициента теплоотдачи , коэффициента излучения и термических сопротивлений. Достоинство метода заключается в простоте техники эксперимента, достаточной точности получаемых результатов и малой продолжительности эксперимента.
198
3.11 Приближенные методы решения задач теплопроводности
В настоящее время существует много различных приближенных методов расчета теплопроводности; которые приводят к удовлетворительным результатам. Приближенные методы решения задач чаще всего применяются в случае, когда точные аналитические методы расчета затруднительны. Рассмотрим некоторые из этих методов.
а) Численный метод.
Аналитические решения, полученные путем непосредственного интегрирования дифференциальных уравнений, дают возможность вычислить температуру в любой точке данной системы. В противоположность этому в основу численного метода положено уравнение в форме конечных разностей, с помощью которого вычисляем температуру в некоторых, заранее выбранных точках данной системы. Это равноценно математическим приемам приближенного интегрирования. Следует отметить, что если получение точного аналитического решения связано с трудностью удовлетворения граничных условий, которые не всегда осуществимы, то при помощи численного метода всегда возможно, по крайней мере приближенно, удовлетворять граничным условиям конкретной задачи.
Из численных методов решения задач теплопроводности в настоящее время наиболее ценным и широко используемым является метод конечных разностей.
Сущность метода заключается в том, что в дифференциальном уравнении производные искомой функции заменяются приближенными соотношениями между конечными разностями в отдельных узловых точках температурного поля. В результате такой замены получаем уравнение в конечных разностях, решение которого сводится к выполнению простых алгебраических операций. Расчетное соотношение приводится к вид, где будущая температура в рассматриваемой узловой точке является функцией времени, настоящей температуры в рассматриваемой точке и настоящей температуры в соседних точках. Такие уравнения составляются для всех узловых точек
198

рассматриваемой области, включая граничные. В результате получаем замкнутую систему алгебраических уравнений. Ввиду однотипности вычислений при решении такой системы представляется широкая возможность для использования современной вычислительной техники.
Для получения расчетных формул при численном интегрировании в настоящее время широко пользуются методом тепловых балансов и математическими операциями при замене в дифференциальных уравнениях производных функций конечными разностями.
В качестве конкретного примера формулу для численного интегрирования одномерной нестационарной задачи методом тепловых балансов. Пусть в этом случае процесс теплопроводности описывается уравнением
dt |
a |
d2 t |
(3.100) |
|
dr |
dx 2 |
|||
|
|
Первым шагом численного метода расчета является разбиение данной системы на соответствующее количество объемов и присвоение номера центральным точкам каждого из этих объемов. Предполагается, что термические свойства каждого такого объема сосредоточены в центральной узловой точке. Передача теплоты между узловыми точками осуществляется через условные тепловыделяющие стержни.
В нестационарном состоянии в каждой точке не только происходит подвод или отвод теплоты. Но и изменяется внутренняя энергия.
Изменение внутренней энергии зависит от изменения температуры в узловой точке во времени, от теплоемкости элементарного объема, который она представляет, и плотности вещества. Такой подход к вычислению температуры носит название метода приближенной численной итерации.
Рассмотрим применение метода к расчету температурного поля в плоской стенке уравн ен ие (3 100) . Для знакомства
с применением численного метода к другим задачам теплопроводности следует обратиться к специальной литературе.
198
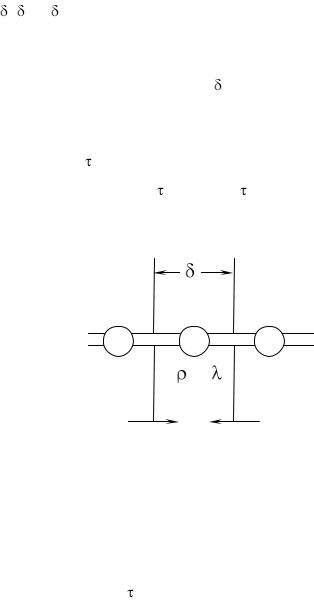
Разбиваем стенку на элементарные объемы
V= × ×1= 2 (рис.3.24). Полагаем, что удельная теплоемкость с и коэффициент теплопроводности λ в пределах элементарного участка постоянны. Очевидно, количество теплоты, подводимое стержнем к узловой точке, определится по закону Фурье: q=. λ (dt/dx). Если расстояние достаточно мало, то можно выразить q через разности, т.е. q=. ( λ / δ ) t, где t – разность температур между смежными узловыми точками. Обще количество теплоты, проводимое стержнем за конечное приращение времени , равно:
Q=q F=- |
λ |
t F, |
(3.101) |
|
δ |
||||
|
|
|
где для одномерной системы проводящая площадь F=,м 2 .
2 |
1 |
3 |
c, |
,V, |
|
Q21 |
|
Q31 |
Рис. 3.24 Разбиение и числовая сетка для нестационарной
одномерной задачи
Изменение внутренней энергии в рассматриваемой узло-
вой точке за время |
|
U=cpV t / =cpV(t / .t), |
(3.102) |
198
