
Методическое пособие 699
.pdfбесчисленного количества явлений выделить конкретно рассматриваемый процесс и дать его полное математическое описание, к дифференциальному уравнению необходимо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти особенности называются условиями однозначности или краевыми условиями.
Условия однозначности включают в себя: геометрические условия, характеризующие форму и
размеры тела, в которых протекает процесс; физические условия, характеризующие распределения
температур в изучаемом теле в начальный момент времени; временные (начальные) условия, характеризующие рас-
пределение температур в излучаемом теле в начальный момент времени;
граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.
Геометрическими условиями задаются форма и линейные размеры тела, в котором протекает процесс.
Физическими условиями задаются физические параметры тела, λ, с, ρ и др. и может быть задан закон распределения внутренних источников теплоты.
Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределения температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть записано следующим образом:
при τ = 0
t=f(x,y,z). |
(1-42) |
В случае равномерного распределения температуры в |
|
теле начальное условие упрощается: |
|
при τ = 0 |
|
t=t0=const. |
(1-43) |
Граничные условия могут быть заданы несколькими способами.
198

а) Граничные условия первого рода. При этом задается распределение температуры на поверхности тела для каждого момента времени:
tс=f(x,y,z, ). |
(1-44) |
где tс – температура на поверхности тела; x,y,z – координаты поверхности тела.
В частном случае, когда температура на поверхности является постоянной на протяжении всего времени протекания процессов теплообмена, уравнение (1-34) упрощается и принимает вид:
tс=const.
б) Граничные условия второго рода. При этом задаются значения теплового потока для каждой точки поверхности тела и любого момента времени.
Аналитически это можно представить следующим об-
разом: |
|
qп=f(x,y,z, ), |
(1-45) |
где qп - плотность теплового потока на поверхности тела; x,y,z
–как и в случае (1-44) – координаты на поверхности тела.
Впростейшем случае плотность теплового потока по поверхности и во времени остается постоянной:
qп= q0=const. |
(1-46) |
Такой случай теплообмена имеет место, например, при нагревании различных металлических изделий в высокотемпературных печах.
в) Граничные условия третьего рода. При этом задается температура окружающей среды tж и закон теплообмена между поверхностью тела и окружающей средой. Граничное условие третьего рода характеризует закон теплообмена между поверхностью и окружающей средой в процессе охлаждения и нагревания тела. Для описания процесса теплообмена между поверхностью тела и средой используется закон НьютонаРихмана.
Процесс теплообмена между поверхностью тела и средой относится к очень сложным процессам и зависит от большого количества параметров.
198

Согласно закону Ньютона-Рихмана количество теплоты, отдаваемое единицей поверхности в единицу времени, пропорционально разности температур поверхности тела tc и окружающей среды tж (tc> tж):
q= ( tc -tж), |
(1-48) |
где - коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м2 К).
Коэффициент теплоотдачи характеризует интенсивность теплообмена между поверхностью тела и окружающей средой. Численно он равен количеству теплоту, отдаваемому (или воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой, равной одному градусу.
Согласно закону сохранения энергии количество теплоты, которое отводится с единицы поверхности в единицу времени вследствие теплоотдачи [уравнение (1-48)], должно равняться теплоте, подводимой к единице поверхности в единицу времени вследствие теплопроводности из внутренних объемов тела, [уравнение (1-10) *], т. е.
t c |
t |
|
t |
, |
(1-49) |
|
ж |
|
|||||
n |
||||||
|
|
|
c |
|
где n – нормаль к поверхности тела; индекс «с» указывает на то, что температура и градиент относятся к поверхности тела
(при n = 0).
Окончательно граничное условие третьего рода можно записать в виде
t |
|
|
t c |
t ж . |
(1-50) |
|
|
|
|||
n |
|
||||
c |
|
|
|||
Уравнение (1-50) по существу является частным выражением закона сохранения энергии для поверхности тела.
Коэффициент теплоотдачи зависит от большого числа факторов. Однако во многих случаях коэффициент теплоотдачи можно считать неизменным, поэтому мы будем в дальнейшем при решении задач теплопроводности принимать величину постоянной.
198
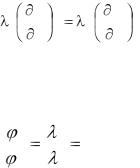
Граничные условия четвертого рода характеризуют условия теплообмена системы тел или тела с окружающей средой по закону теплопроводности. Предполагается, что между телами осуществляется идеальный контакт (температуры соприкасающихся поверхностей одинаковы).
В рассматриваемых условиях имеет место равенство тепловых потоков, походящих через поверхность соприкосновения:
|
t1 |
|
|
t 2 |
. |
(1-51) |
|
1 |
n c |
2 |
n |
||||
|
|
||||||
|
|
|
|
||||
В задачах с граничным условием четвертого рода задается отношение тангенсов угла наклона касательных к температурным кривым в точке соприкосновения тел или тела и среды
(рис. 1-12):
tg |
1 |
|
2 |
const |
(1-52) |
|
tg |
2 |
1 |
||||
|
|
|||||
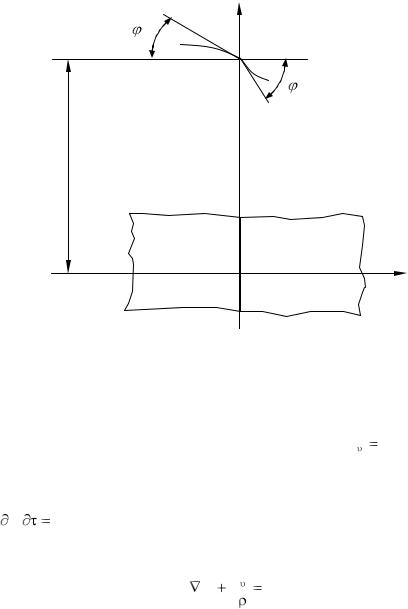
Так как при совершенном контакте оба тела на поверхности соприкосновения имеют одинаковую температуру, то касательные у поверхности раздела проходят через одну и ту же точку (рис. 1-12).
Дифференциальное уравнение (1-39) совместно с условиями однозначности дают полную математическую формулировку конкретной задачи теплопроводности. Поставленная таким образом задача разрешается аналитическим, численным или экспериментальным методом. В случае экспериментального решения задач теплопроводности используются методы физического моделирования или тепловых аналогий (гл. 5 и 6).
198
1 |
t1 |
t |
|
|
|
t2 |
|
|
2 |
|
c |
|
|
) |
|
|
2 |
|
|
(t |
|
|
= |
|
|
c |
|
|
) |
|
|
1 |
|
|
(t |
|
|
1 |
2 |
n |
|
|
|
Рис. 1.3 К граничным условиям четвертого рода |
|
2 ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ |
|
РЕЖИМЕ |
|
2.1 Передача теплоты через плоскую стенку ( q 0 ) |
|
При установившемся, или стационарном тепловом режи- |
ме |
температура тела во времени остается постоянной, т.е. |
t / |
0 . |
|
При этом дифференциальное уравнение теплопроводно- |
сти будет иметь вид:
a 2 t |
q |
0 |
(2-1) |
|
|
||||
c |
||||
|
|
|
или
198

|
|
|
2 t |
|
q |
0 . |
|
(2-1 ) |
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
|
Если внутренние источники теплоты |
отсутствуют |
||||||||||
( q |
0 ), то уравнение (2-1) упроститься и примет вид: |
|||||||||||
|
|
|
|
|
|
2 t |
0 |
|
|
(2-2) |
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
2 t |
|
|
2 t |
|
0 . |
(2-2 ) |
|
|
|
x 2 |
|
|
y2 |
|
z 2 |
|||||
|
|
|
|
|
|
|
||||||
В настоящей главе рассматривается теплопроводность в телах простейшей геометрической формы. При этом случаи,
когда внутренние источники теплоты отсутствуют ( q |
0 ) и |
когда они имеются ( q 0 ), рассматриваются раздельно. Первым объектом рассмотрения является передача теплоты через плоскую стенку при q 0 .
а) Граничные условия первого рода
Рассмотрим однородную и изотропную стенку толщиной  с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживают постоянными
с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживают постоянными
температуры tc1 и tc2.
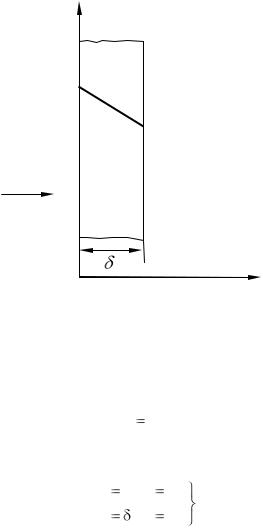
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Если ось Ox направить, как показано на рис. 2-1, то температура в направлении осей Oy и Oz будет оставаться постоянной:
t |
|
t |
0 . |
|
|
|
|
y |
|
z |
|
|
|
198
t
tc1
tc2
q
x
0
Рис. 2.1 Однородная плоская стенка
В связи с этим температура будет функцией только одной координаты x и дифференциальное уравнение теплопроводности для рассматриваемого случая запишется в виде
d 2 t |
0 . |
(2.3) |
|
dx 2 |
|||
|
|
Граничные условия в рассматриваемой задаче зададим следующим образом:
при |
x |
0 t |
t c1 |
; |
(2.4) |
|
при |
x |
t |
t c2. |
|||
|
||||||
Уравнение (2-3) и условия (2-4) дают полную математическую формулировку рассматриваемой задачи.
В результате решения поставленной задачи должно быть найдено распределение температуры в плоской стенке, т.е. t = f(x), и получена формула для определения количества теплоты, проходящего в единицу времени через стенку.
198

Закон распределения температур по толщине стенки найдется в результате двойного интегрирования уравнения (2.3).
Первое интегрирование дает:
dt |
C1 . |
(2.5) |
|
|
|||
dx |
|||
|
|
После второго интегрирования получим:
t C1 x C2 . |
(2.6) |
Из уравнения (2-6) следует, что при постоянном коэффициенте теплопроводности температура в стенке изменяется по линейному закону. Постоянные С1 и С2 в уравнении (2.6) определяются из граничных условий:
при x = 0 t = tc1 и C2 = tc1;
при x = 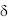 t = tc2 и C1
t = tc2 и C1 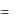 t c1 t c2 .
t c1 t c2 .
Подставляя значения постоянных С1 и С2 в уравнение (2.6), получим закон распределения температуры в рассматриваемой плоской стенке:
t t |
|
t c1 t c2 |
x . |
(2.7) |
|
c1 |
|||||
|
|
|
|||
Если отсчет избыточной температуры в стенке вести от наименьшей заданной температуры tc2, то уравнение (2.7) можно привести в безразмерному виду.
Обозначим t t t c2 - |
текущий температурный напор |
или избыточная температура; |
t 0 t c1 t c2 - полный темпера- |
турный напор или наибольшая избыточная температура. После введения этих обозначений уравнение (2.7) запи-
шется следующим образом: |
|
|
|
|
|
|
|
|
|
t |
t |
|
|
t 0 |
x |
(2.8) |
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
t |
|
1 |
|
x |
. |
|
|
|
t 0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
198
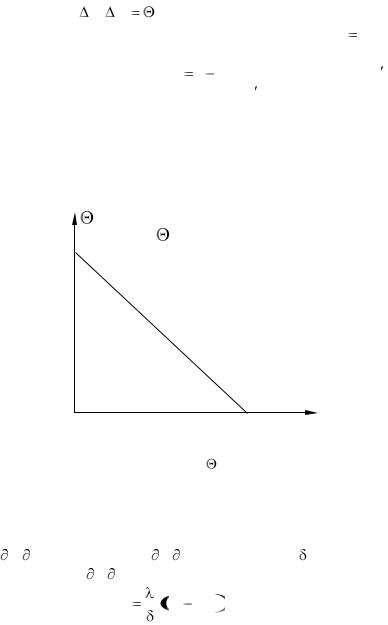
Обозначим t / t 0 |
- безразмерный температурный |
напор или безразмерная избыточная температура x / 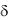 X - безразмерная координата; получим:
X - безразмерная координата; получим:
 1 X. (2.8 )
1 X. (2.8 )
Уравнение температурного поля (2.8 ) является универсальным. Его универсальность заключается в том, что распределение температуры в стенке можно представить единой прямой в отрезках на осях для любого заданного значения tc1, tc2 и 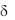 (рис. 2.2). В ряде случаев пользоваться безразмерными уравнениями весьма удобно.
(рис. 2.2). В ряде случаев пользоваться безразмерными уравнениями весьма удобно.
= 1 - x
1
0 1
Рис. 2.2 Безразмерное поле температур в плоской стенке = 1 - x
Для определения количества теплоты, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ox, воспользуемся законом Фурье, согласно которому
q = - 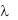 t/ x. Учитывая, что t/ x= C1 = (tc1 – tc2)/ , после подстановки значения t/ x в выражение закона Фурье получим:
t/ x. Учитывая, что t/ x= C1 = (tc1 – tc2)/ , после подстановки значения t/ x в выражение закона Фурье получим:
q |
|
t c1 t c2 . |
|
Из уравнения (2.9) следует, что количество теплоты, проходящее через единицу поверхности стенки в единицу време-
198

ни, прямо пропорционально коэффициенту теплопроводности , разности температур на наружных поверхностях стенки tc1 – tc2 и обратно пропорционально толщине стенки . Следует указать, что тепловой поток определяется не абсолютным значе-
нием температур, а их разностью tc1 – tc2 = |
t, которую принято |
называть температурным напором. |
|
Отношение / , Вт/(м2 К) называют тепловой проводи- |
|
мостью стенки, а обратная величина / , |
м2 К/Вт - тепловым |
или термическим сопротивлением стенки. Последнее представляет собой падение температуры в стенке на единицу плотности теплового потока. Зная плотность теплового потока, легко вычислить общее количество теплоты Q , которое передается через поверхность стенки величиной F за промежуток времени :
Q |
qF |
|
|
(t c1 t c2 )F . |
(2.10) |
||||
|
|
||||||||
Из уравнения (2.9) найдем: |
|
|
|
|
|
|
|||
|
t c1 |
t c2 |
|
q |
. |
|
|||
|
|
|
|
|
|
|
|
||
После введения этого выражения в уравнение темпера- |
|||||||||
турного поля (2.7) получим: |
|
|
|
|
|
|
|
|
|
|
|
t t c1 |
|
|
q |
x . |
(2.11) |
||
|
|
|
|
|
|||||
Из уравнения (2.11) следует, что при прочих равных условиях температура в стенке убывает тем быстрее, чем больше плотность теплового потока.
Выражения (2.7) и (2.9) получены в предположении, что = const. В действительности является переменной величи-
ной.
Рассмотрим случай, когда коэффициент теплопроводности является функцией температуры:
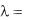 (t) .
(t) .
Для многих материалов зависимость коэффициента теплопроводности от температуры близка к линейной:
198
