
Методическое пособие 699
.pdf
где t- температура в данной узловой точке в момент времени ;
t / - температура в момент времени |
+ |
|
|
|
|
|
; c - удельная тепло- |
|||||||||||||||||||||||||||
емкость; p - плотность вещества; V - элементарный объем. |
||||||||||||||||||||||||||||||||||
На основании сказанного уравнение теплового баланса |
||||||||||||||||||||||||||||||||||
для узловой точки 1 (рис.3.24) будет иметь вид: |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Q |
|
+Q |
|
|
= |
cpV |
(t /1 |
.t |
|
|
) |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
21 |
31 |
|
1 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
λ |
(t |
|
- t |
|
) ×1+ |
λ |
(t |
|
- t |
|
) |
|
×1= |
cpV |
(t / 1 -t |
|
). |
||||||||||||||||
|
δ |
1 |
|
2 |
|
|
|
δ |
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
τ |
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решая последнее уравнение относительно неизвестной |
||||||||||||||||||||||||||||||||||
температуры t / 1 , получаем; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
t / 1 = |
|
τλ |
(t |
|
|
+ t |
|
+ |
|
|
1 |
|
|
-2t |
|
) |
|
(3.103) |
||||||||||
|
|
|
|
|
|
|
|
2 |
3 |
|
|
τλ |
|
|
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
cpV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
срV |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если учесть, |
что |
λ / cp |
|
|
|
a |
|
|
коэффициент |
температуро- |
||||||||||||||||||||||||
проводности вещества, |
V= δ2 |
|
и |
|
|
|
а/ δ2 =Fo. число Фурье, то |
|||||||||||||||||||||||||||
уравнение (3.103) принимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
t / 1 =Fo t 2 |
|
|
|
|
t 3 |
|
|
t1 |
1 |
|
|
|
2 |
|
(3.104) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Fo |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Уравнение (3.104) является основой численного метода расчета нестационарной теплопроводности. Для расчета тем-
пературы t / 1 по (3.104) необходимо выбрать определенное значение Fo. При этом важно помнить, что выбор Fo ограничен условием
Fo |
1 |
|
(3.105) |
2 |
|
||
|
|
|
|
Как показывает анализ, только при этом обеспечивается |
|||
устойчивость уравнения (3.104). Если же Fo |
1 2 т.е. нару- |
||
шить условие (3.105), то изменение температуры в процессе расчета приобретает беспорядочный скачкообразный характер и расчет перестает быть верным. Поэтому при выборе проме-
198
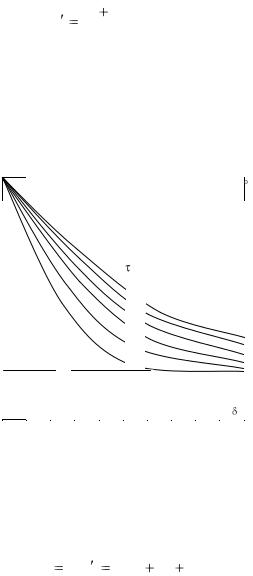
жутков δ и τ необходимо заботиться о том, чтобы условие
(3.105) выполнялось. Если выбрать δ и |
τ из условий Fo =1/2, |
||
то уравнение (3.104) принимает вид: |
|
||
t1 |
t 2 t3 |
(3.106) |
|
2 |
|
||
|
|
|
|
Формула (3.106) широко используется при графическом решении нестационарных задач теплопроводности. При этом будущая температура данной узловой точки не зависит от ее настоящей. При других значениях Fo уравнение (3.104) приводит к более сложным результатам:
|
|
|
|
|
t - C |
|
|
|
|
|
-200 |
|
|
|
мин |
|
-150 |
|
|
|
1,8 |
|
|
|
|
|
1,5 |
|
|
|
|
|
1,2 |
|
-100 |
|
|
|
0,9 |
|
|
|
|
|
0,6 |
|
|
|
|
|
0,3 |
|
-50 |
|
t |
|
|
37,7 |
|
|
|
|
|
||
|
|
|
|
|
-0 |
|
|
|
|
|
x/ |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
Рис. 3.25 Сравнения численных расчетов с точным решением распределения температур (Fo=1/4) в плоской стенке. Линии соответствуют аналитическому решению, точки . численному расчету
Fo |
1 |
, t2 |
1 |
|
(t1 t 2 t 3 ) |
(3.107) |
|
3 |
3 |
||||||
|
|
|
|
||||
и
198

Fo = |
1 |
, t |
1 |
(t3 t 2 2t1 ). |
(3.108) |
|
4 |
4 |
|||||
|
|
|
|
Из уравнений (3.106) - (3.108) следует, что уменьшение значений Fo увеличивает число вычислений и густоту сетки, однако при этом повышается точность вычислений.
4
1 |
0 |
3 |
y |
|
|
|
2 |
|
|
|
x |
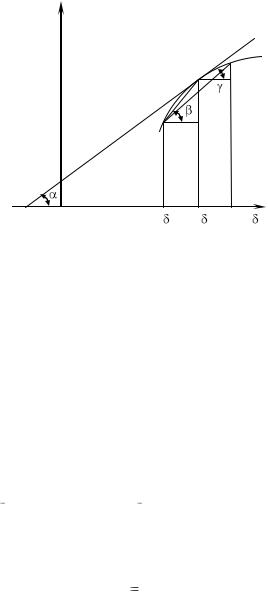
Рис. 3.26 Сетка узловых точек для двухмерной нестационарной задачи
Для случая, когда одна из поверхностей пластины изолирована и на ней не происходит теплообмена, а на другой коэффициент теплоотдачи α  уже при выборе Fo=1/4 приближенный численный метод практически не отличается от тонкого расчета. Сравнение таких расчетов приведено на рис.3.25. Пользуясь изложенным методом, можно получить исходное уравнение для численного расчета и для других задач нестационарной теплопроводности. В частности, для двухмерной задачи после разбиения тела на элементарные объемы с размерами ячеек х= у= δ схема узловых точек будет выглядеть, как показано на рис.3.26. Составляя уравнение теплового баланса для центральной точки, получаем:
уже при выборе Fo=1/4 приближенный численный метод практически не отличается от тонкого расчета. Сравнение таких расчетов приведено на рис.3.25. Пользуясь изложенным методом, можно получить исходное уравнение для численного расчета и для других задач нестационарной теплопроводности. В частности, для двухмерной задачи после разбиения тела на элементарные объемы с размерами ячеек х= у= δ схема узловых точек будет выглядеть, как показано на рис.3.26. Составляя уравнение теплового баланса для центральной точки, получаем:
198
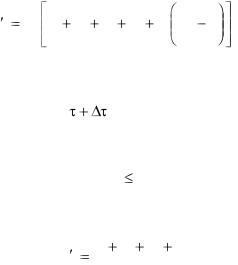
t 0 Fo t1 t 2 |
t 3 |
t 4 |
|
t 0 |
1 |
4 , |
(3.109) |
||
|
|
||||||||
F |
|||||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
|
|
где t o, t1 ,t 2 t 3 ,t 4 - температура |
в |
|
соответствующей узловой |
||||||
точке в момент времени |
τ ; t 0 |
/ - |
|
температура в центральной |
|||||
точке в момент времени |
. |
|
|
|
|
|
|
|
|
Для этой двухмерной задачи промежутки δ и |
τ должны |
||||||||
выбираться из условия |
|
|
|
|
|
|
|
|
|
|
Fo |
|
1 |
|
|
|
(3.110) |
||
|
4 |
|
|
|
|||||
|
|
|
|
|
|
||||
аналогично условию (3.105) для одномерной задачи.
При значении Fo=1/2 уравнение (3.109) принимает вид:
t |
|
t1 t 2 |
t3 |
t 4 |
(3.111) |
0 |
|
4 |
|
||
|
|
|
|
|
При этом будущая температура узловой точки не зависит от ее настоящей.
Для замены производных функции в дифференциальном равнении разностными отношениями можно воспользоваться математическими операциями. Такой подход не является более строгим, но он дает возможность решать задачи при разнообразных краевых условиях, оценить погрешность перехода от дифференциального уравнения к уравнению в конечных разностях и более просто провести анализ условий устойчивости и сходимости решения.
198
t
|
B |
C |
|
K |
|
|
m |
|
A |
m E |
|
D
m |
|
x |
0 |
(m-1) x |
m x (m+1) x |
|
Рис.3.27 К выводу формул для замены первой и второй производной разностными отношениями
Получим приближенную замену первой и второй производной через разностные отношения некоторой функции t=f(x), где под х можно понимать любую независимую переменную.
Прежде всего интервал изменения функции разобьем на одинаковые участки δ x .
Каждая точка будет иметь свою абсциссу, отличающуюся на величину δ x . иначе говоря, координату точки x m заменим
m δ x . (m = 1,2,3,….). Отметим на кривой t=f(x), точки А (t m , m δ x . ), B(t m 1, (m.1) δ x . ) и C (t m 1, (m+1) δ x . ).
Касательная в точке А (t m , m δ x . ), образует угол α m с положительным направлением оси абсцисс, тогда производная функции для рассматриваемой точки А (t m , m δ x . )
t / |
m |
tg α m . |
(3.112) |
Если интервал разбиения δ x . .величина малая, то с доста- |
|||
точным приближением угол |
α m можно заменить |
углами |
|
|
198 |
|
|
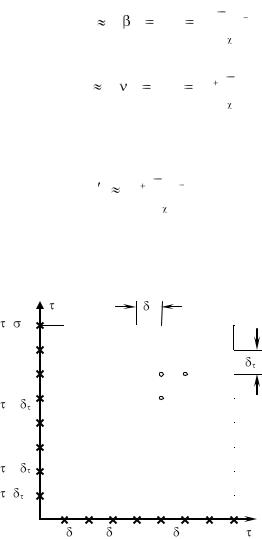
β m или ν m (см. рис.3.27) , образованными секущими ВА и АС. При этом производная в точке А (t m , m δ x . ) запишется следующим образом:
t |
/ |
|
tg |
|
|
AE |
|
t m |
t m 1 |
(3.113) |
|
|
m |
m |
|
BE |
|
g |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
tg |
|
CK |
|
t m 1 |
t m |
. |
(3.114) |
|
|
m |
m |
AK |
|
g |
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
Если угловой коэффициент касательной AD заменить на угловой коэффициент секущей ВС, получим выражение для производной в точке А следующего вида:
t |
|
t m 1 t m 1 |
. |
(3.115) |
m |
|
|||
|
2g |
|
||
|
|
|
||
Полученные выражения (3.113).(3.115) равноценны ля замены первой производной функции и называются соответственно: предыдущее, последующее и симметричное разностные отношения.
|
|
|
x |
|
|
= |
|
|
|
|
|
|
|
|
2 |
3 |
|
=k |
|
|
1 |
|
|
=2 |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
x |
0 |
x= x |
x=2 x |
x=m x |
x=m |
|
|
|||||
Рис. 3.28 К получению расчетной сетки и |
|||||
составлению уравнений для узловых точек |
|||||
198

Если заменить кривую на участке ВС ломаной ВАС, имеющей в точке А два наклона, то получим выражение для торой производной функции t=f(x):
t |
1 t m 1 |
t m |
|
t m t m 1 |
1 |
t m 1 |
t m 1 2t m . (3.116) |
|||||
g |
x |
|
g |
x |
|
g |
x |
|
g2 x |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Приведенные формулы (3.114)-(3.116) наиболее часто используются при численном интегрировании уравнений теплопроводности. Используем полученные формулы для преобразования дифференциального уравнения к конечно.разностной форме. Преобразование проведем на примере одномерной нестационарной задачи теплопроводности безграничной стенки
уравн ен ие(3 100) :
dt |
|
d 2 t |
|
|
a |
|
. |
d |
dx 2 |
||
Так как температура t(x, τ) является функцией двух пере-
менных, удобно выбрать прямоугольную сетку. Весь интервал х от 0 до l по оси абсцисс разобьем на одинаковые интервалы δ x . а отрезок времени от τ 0 до  = разделим на равномер-
= разделим на равномер-
ные интервалы δ τ (рис.3.28). Восстановленные перпендикуля-
ры к координатным осям в точках деления при пересечении образуют расчетные узловые точки. Тогда температура для уз-
ловой точки l с координатами |
x |
mδx и |
τ |
kδ τ , запишется |
||||||||
так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t1 |
|
t1 m x , k |
tm,k . |
|
|
|
|
|
|
Для точки 2 с координатами x = m x |
и |
τ |
δ τ |
k |
1 δ x |
|||||||
имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
t2 m x k 1 |
tm, k 1 ; |
|
|
|
||||
для |
точки |
3 |
с |
координатами |
x |
x |
m |
1 x |
и |
|||
k |
1 |
получим |
|
|
|
|
|
|
|
|
||
t3 |
t3 |
m 1 |
x |
k |
1 |
tm 1,k 1 и т.д. |
|
|
|
|
||
198
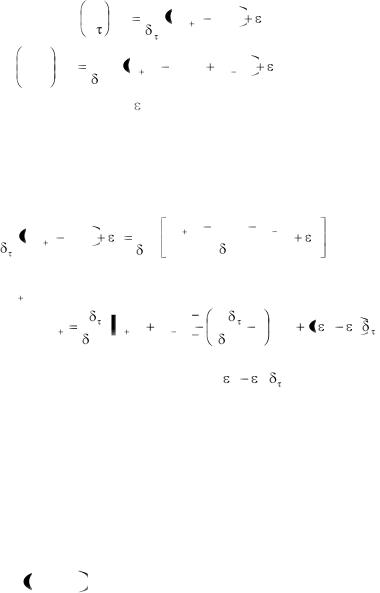
Заметим в точке 1 (m δx , k δτ ) частные производные в уравнении теплопроводности разностными отношениями:
|
|
|
|
dt |
|
|
|
1 |
t m,k 1 |
t m,k |
1 ; |
(3.117) |
||
|
|
|
|
d |
|
|
m,k |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d2 t |
1 |
|
t m 1,k |
2t m,k |
t m 1,k |
|
(3.118) |
||||||
|
dx |
|
|
|
|
|
|
|
2. |
|||||
|
2 |
m,k |
|
2 x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
В этих выражениях 1 , |
ε3 - остаточные члены, |
учиты- |
||||||||||||
вающие переход от производных функций к разностным отношениям. Можно показать, что эти члены стремятся к нулю при стремлении к нулю интегралов разбиения δx и δτ. . Диффе-
ренциальное уравнение в конечно-разностной форме запишется следующим образом:
1 |
t m,k 1 |
t m,k |
|
|
a |
|
|
t m 1,k |
|
2t m,k |
t m 1,k |
|
(3.119) |
|||
|
|
1 |
|
2 |
|
|
|
2 x |
|
|
2 |
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решая уравнение (3.119) относительно будущей темпера- |
||||||||||||||||
туры t m,k 1 в рассматриваемой точке, получаем: |
|
|
||||||||||||||
|
|
t m,t 1 |
a |
|
t m 1,k |
t m 1,k |
|
2a |
1 t m,k |
a 2 |
1 . . |
|||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
2 x |
|||||||||||
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.120) |
Очевидно, |
остаточный |
член |
(a 2 |
1 ) в |
уравнении |
|||||||||||
(3.120) будет стремиться к нулю при стремлении к нулю δτ .
Следовательно, чем более мелкие интервалы выбраны для сетки узловых точек, тем меньше ошибка перехода от дифференциального уравнения к уравнению в конечных разностях. Ошибки ε1 и ε2 можно оценить, воспользовавшись разложени-
ем функции t в ряд Тейлора.
Отбрасывая остаточный член в уравнении (3.120) и обозначая приближенное значение величины t m,k через Tm,k, полу-
чим приближенное решение для будущей температуры в узловой точке mδx,kδτ :
198

Tm,k 1 |
a |
|
Tm 1,k |
Tm 1,k |
2a |
1 Tm,k . |
(3.121) |
|
|
|
|||||
2 |
|
2 x |
|||||
|
ч |
|
|
|
|||
В уравнении |
(3.121) |
комплекс a / |
2 x Fo имеет |
смысл |
|||
числа Фурье для элементарного объема расчетной области, тогда
Tm,k 1 Fo Tm 1,k Tm 1,k 2Fo 1 Tm,k. |
( 3 121 ) |
Если нам известно распределение температуры в расчетной области в какой-либо (например, начальный) момент времени, то. Пользуясь системой уравнений полученного типа, можно рассчитать температуру в узловых точках для последующего момента времени τ δ τ. Температура в узловых точ-
ках, находящихся на границах области интегрирования, известна из граничных условий.
Из уравнения (3.121) следует. Что значения расчетных температур зависят от числа Fo, т.е. от способа разбиения про- странственно-временной области. Выбирая интервалы разбиения δ x и δ τ , мы можем получить любое значение числа Fo. Од-
нако, как показывает анализ, решение устойчиво не при любом значении Fo, а следовательно, выбор величин δ x и δ τ не произ-
волен. Анализ отклонения числового расчета от точного решения показывает, что устойчивость расчета для рассматриваемой задачи обеспечивается только при том условии, когда в
уравнении (3.120) |
|
|
(2Fo-1) |
0 |
(3.122) |
Выражение (3.122) является основным условием, кото- |
||
рое ограничивает произвольный |
выбор |
интервалов сет- |
ки δ x и δ τ . Точно такое же условие обеспечения численного ин-
тегрирования было получено методом тепловых балансов (выражение (3.105)).
Нетрудно получить конечно-разностное выражение и для двухмерной нестационарной задачи теплопроводности t(x,y, ). Дифференциальное уравнение для такой задачи имеет вид:
198

d t |
a |
d2 t |
|
d2 t |
. |
(а) |
d |
dx2 |
|
dy2 |
|||
|
|
|
|
В этом случае температуре для любой узловой точки должно присваиваться три индекса t k где m, n, . индексы координат, k.индекс времени. Разобьем область интегрирования на одинаковые интервалы. Тогда. Пользуясь ранее полученными соотношениями, для узловой точки с координатами
y , k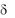 получим:
получим:
dt
d
k |
1 |
|
|
|
|
|
t k 1 |
t k |
|
; |
|
|
|
1 |
|||
|
|
m,n |
m,n |
|
m,n
|
d 2 t |
k |
1 |
|
t mk 1,n |
t mk 1n |
2t m,nk |
2 ; |
|||
|
dx 2 |
m,n |
2 |
|
|||||||
|
|
|
x |
|
|
|
|
|
|||
|
d 2 t |
|
k |
|
1 |
|
t m,nk |
|
t m,nk |
1 2t m,nk |
3 . |
|
dy |
|
|
2 y |
1 |
||||||
|
m,n |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
Подставляя полученные выражения для производных (без |
|||||||||||
остаточных членов |
ε1, ε2, ε3 ) |
в дифференциальное уравнение |
|||||||||
(а), получаем приближенное выражение для будущей темпера-
туры в точке |
m |
m , n |
y , k |
|
: |
|
|
|
|
|
|
|
|
|
||||||
|
1 |
T k 1 |
T k |
|
a |
T k |
|
T k |
|
2T k |
|
|
a |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
m,n |
|
m,n |
2 |
|
m 1,n |
m 1,n |
m,n |
2 |
|
|
(3.124) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
y |
|
|||
|
T k |
T k |
|
2T k . |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
m,n 1 |
|
m,n 1 |
|
|
|
m,n |
|
|
|
|
|
|
|
|
|
|
|
Полагая δx |
δy и решая (3.124) |
относительно |
|
будущей |
||||||||||||||||
температуры в рассматриваемой узловой точке, получаем: |
||||||||||||||||||||
Tk 1 |
|
a |
Tk |
|
Tk |
|
Tk |
Tk |
|
4a |
1 Tk |
|
. (3.124 ) |
|||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
m,n |
2 |
|
m 1,n |
|
m 1,n |
|
m,n 1 |
m,n 1 |
2 x |
|
m,n |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначая, как и в предыдущем случае, |
a / |
|
2x Fo, то |
|||||||||||||||||
выражение (3.124 ) приводим к виду |
|
|
|
|
|
|
|
|||||||||||||
Tk 1 |
|
Fo Tk |
|
Tk |
|
Tk |
|
Tk |
|
4Fo |
1 Tk |
. (3.124 ) |
||||||||
|
m,n |
|
|
m 1,n |
|
m 1,n |
m,n 1 |
m,n 1 |
|
|
|
m,n |
|
|
||||||
198
