
Методическое пособие 699
.pdf
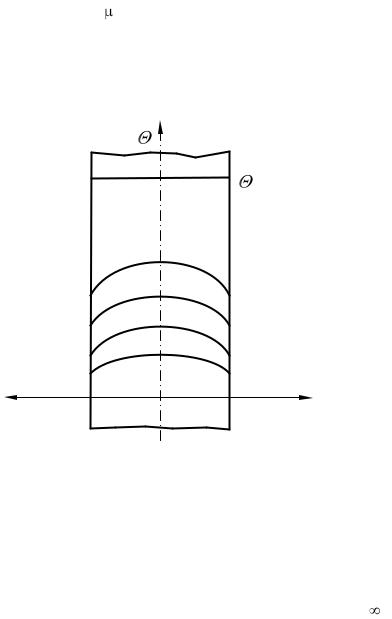
Из уравнения (3.24) следует, что в условиях охлаждения (нагревания) пластины для любого момента времени при заданных граничных условиях поле температуры имеет вид симметричной кривой с максимумом на оси пластины (Х = 0). Для каждого последующего момента времени будет своя кривая, монотонно убывающая к поверхностям пластины. При этом для любого момента времени касательные к кривым в точках Х = ± 1 проходят через две направляющие точки + А и
– А . расположенные на расстоянии ± Х0 от поверхности пла-
стины, X0 = 1/Bi (рис. 3.6).
Для доказательства этого важного свойства рассмотрим температурное поле для произвольного момента времени
Fo>0.
Умножив граничнoe условие (3.6) при x = 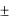 на / 0, получим:
на / 0, получим:
|
0 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
x |
0 |
|||||
|
x |
||||||
|
|
|
|||||
x
Записывая последнее выражение в безразмерных величинах, будем иметь:
|
Bi X 1 . |
(а) |
|
X |
|||
X 1 |
|
Из рисунка следует, что
|
|
X 1 |
tg . |
(б) |
||
X |
X 1 X |
0 |
||||
|
|
|||||
Сравнивая выражения (а) и (б), получаем:
X0 |
1 |
. |
(3.29) |
|
|||
|
Bi |
|
|
Из уравнения (3.29) следует, что расстояние точки А от поверхности определяется заданными условиями однозначности, которые справедливы для любого момента времени. Следовательно, касательные ко всем температурным кривым в
198

точке пересечения с поверхностью пластины и неизменных граничных условиях всегда будут проходить через точку А. Сказанное справедливо не только для пластины, но и для цилиндра, шара и тел других геометрических форм.
= 1; F0 = 0
F01 > F0
F02 > F01
x = 0 |
|
= 1 |
|
|
x |
- x - А |
|
+ А + x |
|
|
0 |
- x0 |
2 |
+ x0 |
Рис. 3.6 Изменение температурного поля в плоской неограниченной стенке при ее охлаждении
Доказанное свойство температурных кривых дает возможность определить характер изменения температуры в теле при заданном значении числа Bi. Рассмотрим при этом три случая.
1. Случай, когда Bi 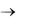 (практически Bi > 100). Если число Bi стремится к бесконечности, то температура поверхности пластины сразу становится равной температуре окружающей среды, в которую помещена пластина. Последнее видно из уравнения (3.29): при Bi
(практически Bi > 100). Если число Bi стремится к бесконечности, то температура поверхности пластины сразу становится равной температуре окружающей среды, в которую помещена пластина. Последнее видно из уравнения (3.29): при Bi 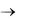 X0 = 1/Bi = 0. Это озна-
X0 = 1/Bi = 0. Это озна-
198
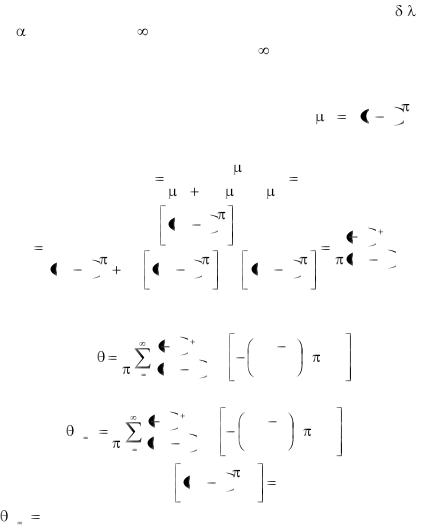
чает, что точка пересечения касательных к температурным кривым находится на поверхности пластины. Из Bi = ( / ) / (1/ ) следует: Bi  при заданных физических параметрах и толщине пластины тогда, когда
при заданных физических параметрах и толщине пластины тогда, когда 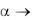 , т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физически-
, т.е. когда имеет место очень большая интенсивность отвода теплоты от поверхности. В этих случаях процесс охлаждения определяется физически-
ми свойствам и размерами тела. |
При этом |
|
n |
2 n |
1 |
|
, и |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тогда коэффициент ряда (3.24): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
D n |
|
|
|
|
2 sin |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
cos |
n sin |
n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 sin |
2n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1 n 1 |
||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
2n |
1 |
|
|
|
sin |
|
2n |
1 |
|
|
cos 2n |
1 |
|
|
|
|
|
|
|
2n |
1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Общее решение для рассматриваемого случая принимает |
||||||||||||||||||||||||||||||||||||
вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
1 n |
1 |
exp |
|
|
|
2n |
1 |
|
2 |
|
2 Fo |
. |
(3.30) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
n |
1 2n |
|
1 |
2 |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Тогда температура на оси пластины (X = 0) |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
1 n |
1 |
|
exp |
|
|
2n |
1 2 |
|
|
2 Fo . |
|
(3.31) |
||||||||||||||
|
|
|
X |
0 |
|
|
|
|
|
2n |
1 |
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
При |
Х |
= |
1 |
|
cos |
2n |
1 |
|
X |
0 , |
|
|
и, следовательно, |
|||||||||||||||||||||||
|
|
2 |
|
|
|||||||||||||||||||||||||||||||||
X 1 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
198
F0 = 0 |
|
= 1 |
|
F01 |
|
|
F02 |
|
|
F03 |
|
- x |
F04 |
+ x |
|
||
|
0 |
|
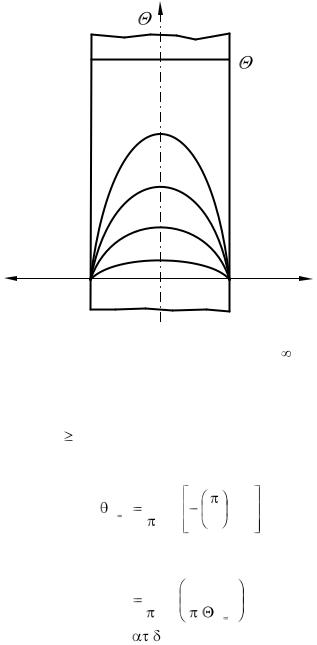
Рис. 3.7 Распределение температуры в плоской стенке при ее охлаждении в условиях Bi 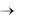 ; F01 <
; F01 <
F02 < F03 < F04
Распределение температуры в пластине при Fo > 0 показано на рис. 3.7; здесь Fo1 < Fo2 < Fo3 < Fo4 < ... < Fon. Как было сказано, при Fo 0,3 ряд (3.24) быстро сходится и ошибка не превышает 1%, если отбросить все члены ряда, кроме первого. При этих условиях уравнение (3.31) принимает вид:
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
|
exp |
|
|
Fo . |
(3.32) |
|||||
X 0 |
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Если уравнение (3.32) прологарифмировать и решить от- |
|||||||||||
носительно числа Fo, то получим: |
|
|
|
|
|||||||
Fo |
|
4 |
ln |
4 |
|
|
1 |
. |
(3.33) |
||
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
X 0 |
|
||
Учитывая, что Fо = |
/ 2, уравнение (3.33) можно запи- |
||||||||||
сать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
198 |
|
|
|
|
|
|
|
||

2 |
2 |
1 |
ln |
4 |
|
1 |
. |
(3.33 ) |
|
a |
|
X 0 |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
По формуле (3.33) можно определить время, необходимое для прогрева середины пластины до заданной температуры.
2. Очень малые числа Bi (практически Bi < 0,1). Если
число Bi мало, то все коэффициенты членов ряда Dn |
0, по- |
|||||||
скольку теперь n = (n-1) |
, за исключением D1, который равен: |
|||||||
D1 |
|
|
2 sin |
1 |
|
|
1. |
|
|
1 |
sin |
1 cos |
1 |
|
|
||
|
|
|
0 |
|
||||
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
Из выражения Bi = ( / ) / (1/ |
) видно, что малые значе- |
|||||||
ния числа Bi могут иметь место при малых размерах толщины пластины, при больших значениях коэффициента теплопроводности и малых значениях коэффициента теплоотдачи . Следует заметить, что при малых значениях 1 функции tg 1 и sin 1 можно заменить через их аргументы, и тогда характеристическое уравнение (3.14) запишется:
1 |
|
1 |
. |
|
|
|
|
||
|
|
|
||
1 |
|
Bi |
||
|
|
|
||
Учитывая сказанное, уравнение (3.24) можно переписать |
||||
так: |
|
|
|
|
|
|
|
|
2 Fo |
|
|
|
|
|
|
cos |
1 |
X exp |
|
cos BiX exp BiFo . |
(3.34) |
|||||
|
|
|
1 |
|
|
|
|
|
|
|
Найдем температуры на оси и па поверхности пластины: |
||||||||||
при X = 0 |
X = 0 = exp (.Bi Fo); |
(3.35) |
||||||||
|
|
|
|
|
|
|
||||
при Х = 1 |
X 1 |
cos |
|
Bi exp BiFo . |
(3.36) |
|||||
|
|
|
|
|
|
|
|
|
|
|
Отношение температур на оси и поверхности пластины |
||||||||||
X 0
X 1
exp BiFo |
1. |
|||
|
|
|
||
|
|
|
||
cos Bi exp BiFo |
||||
|
||||
198
F0 = 0 |
= 1 |
|
F01 |
|
F02 |
|
F03 |
|
F04 |
- x |
+ x |
|
0 |
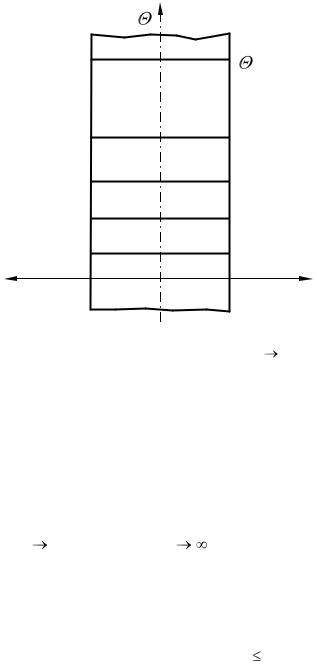
Рис. 3.8. Распределение температуры в плоской стенке при ее охлаждении в условиях Bi 0; F01 <
F02 < F03 < F04
При малых Bi температура на поверхности пластины незначительно отличается от температуры на оси. Это указывает на то, что температура по толщине пластины распределяется равномерно и кривая температур остается почти параллельной оси ОХ для любого момента времени (рис. 3.8).
Касательные к температурным кривым в точках пересечения их с поверхностью должны пересекаться с осью абсцисс
в бесконечности: |
|
при Bi 0 имеем Xo = 1/Bi |
. |
В рассматриваемом случае процесс нагрева и охлаждения тела определяется интенсивностью теплоотдачи на поверхности пластины. Иначе говоря, процесс выравнивания температуры в теле происходит существенно интенсивнее, чем отвод теплоты с поверхности. Задача становится внешней.
3. Число Bi находится в пределах 0,1 Bi < 100. В рас-
198
сматриваемом случае n есть функция Bi, т. е. зависит от толщины пластины. Температурные кривые для любого момента времени будут выглядеть, как показано на рис. 3.9. В этом случае интенсивность процесса охлаждения (нагревания) определяется как внутренним, так и внешним термическими сопротивлениями.
F0 = 0 |
= 1 |
|
F01 |
|
F02 |
|
F03 |
|
F04 |
- x |
+ x |
|
0 |
Рис. 3.9 Распределение температуры в плоской стенке при ее охлаждении в условиях, когда Bi – конечная величина; F01 < F02 < F03 < F04
3.4 Определение количества теплоты, отданного пластиной в процессе охлаждения
Количество теплоты Qп, Дж, которое отдает или воспринимает пластина с обеих сторон за время от 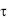 = 0 до
= 0 до 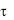 = , должно равняться изменению внутренней энергии пластины за период полного ее охлаждения (нагревания):
= , должно равняться изменению внутренней энергии пластины за период полного ее охлаждения (нагревания):
198

Qp 2 f c t 0 t ж . |
(3.37) |
Тогда за любой промежуток времени от 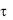 = 0 до 1 или, что то же, от Fo до Fo1, внутренняя энергия пластины изменится на
= 0 до 1 или, что то же, от Fo до Fo1, внутренняя энергия пластины изменится на
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q Qп Q1 |
2 f c t 0 t ж |
1 |
|
|
t1 |
t ж |
, |
||
|
|
|
t 0 |
t ж |
|||||||
|
|
|
|
|
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
||
|
|
|
Q Qп 1 |
|
|
, |
|
|
|
|
(3.38) |
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
||||||||
где Q1 t1 t ж / t 0 |
t ж средняя безразмерная температура |
||||||||||
по толщине пластины в момент времени |
1. |
|
|
|
|
||||||
Из соотношений (3.37) и (3.38) следует, что расчет количества теплоты, отданного или воспринятого пластиной, сводится к нахождению средней безразмерной температуры в интересующий нас момент времени. Средняя безразмерная температура для слоя пластины от оси симметрии до плоскости Х найдется как
1 |
X |
|
|
dX |
|
X |
||
0 |
в соответствии с теоремой о среднем.
Если в это выражение подставить под знак интеграла значение из уравнения (3.24) и проинтегрировать в пределах от нуля до единицы, то получим:
|
|
2 sin2 |
|
|
2 Fo . |
|
|
|
n |
|
exp |
(3.39) |
|
2 |
|
|
||||
n sin n cos |
|
|
n |
|
||
n 1 n |
n |
|
|
|||
Подставив в уравнение (3.38) вычисленное по формуле (3.39) значение средней температуры пластины для интересующего нас момента времени, получим количество теплоты, отданное пластиной в окружающую среду за рассматриваемый промежуток времени.
При Bi 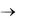 (практически Bi > 100) уравнение (3.39) принимает вид:
(практически Bi > 100) уравнение (3.39) принимает вид:
198

|
|
|
|
|
|
8 |
|
|
|
|
|
2n |
1 |
2 |
|
|
|||
|
|
|
|
|
|
|
|
|
exp |
|
2 Fo . |
(3.40) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n 1 |
2 |
2n |
1 2 |
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
Если Bi |
|
0 (практически Bi < 0,l), уравнение (3.39) при- |
|||||||||||||||||
нимает вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
exp |
BiFo . |
|
|
(3.41) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
При значениях числа Fo |
0,3 для пластины можно огра- |
||||||||||||||||||
ничиться первым членом ряда (3.39), тогда |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2sin2 |
1 |
|
|
exp |
2 Fo . |
(3.42) |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 sin |
1 cos |
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||||
Множитель 2 sin2 |
1/( 21 + |
1 cos |
|
1 sin |
1) зависит только |
||||||||||||||
от числа Bi и может быть представлен как некоторая функция M(Bi), тогда уравнение (3.42) запишется:
M Bi exp |
12 Fo . |
(3.42 ) |
Функция M(Bi) может быть заранее рассчитана и представлена в таблицах. Тогда расчет средней температуры будет сводиться к вычислению экспоненты.
3.5 Охлаждение (нагревание) бесконечно длинного цилиндра
Цилиндр радиусом го отдает тепло окружающей среде через свою боковую поверхность; коэффициент теплоотдачи 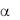 во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды tж постоянна. В начальный момент времени при
во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды tж постоянна. В начальный момент времени при 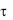 = 0 температура является некоторой функцией t (r, 0) = f(r). Отсчет температуры цилиндра будем вести, как и в § 3.3, от температуры среды, т. е. t – tж = . При этих условиях уравнение теплопроводности принимает вид:
= 0 температура является некоторой функцией t (r, 0) = f(r). Отсчет температуры цилиндра будем вести, как и в § 3.3, от температуры среды, т. е. t – tж = . При этих условиях уравнение теплопроводности принимает вид:
2 |
1 |
|
|
|
|||
a |
|
|
. |
(3.43) |
|||
|
|
|
|
|
|||
r 2 |
|
r r |
|||||
|
|
|
|
||||
Граничные и начальные условия: при = 0 и 0 r r0
198
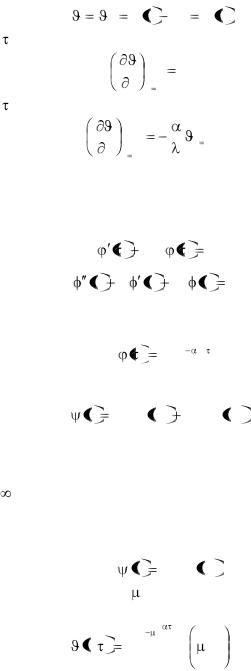
0 |
|
f |
r |
|
t ж F r ; |
|||
при > 0 и r = 0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
0 ; |
||
|
|
|
r |
|
||||
|
|
|
r |
0 |
|
|
||
при > 0 и r = r0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
r r . |
|
r |
r r |
|
|
||||
|
|
0 |
||||||
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
Сформулированную задачу решим с помощью разделения переменных, т. е. 0'(г, т) ==ф(т)ф(г). Подставляя это выражение в уравнение (3.43), получим два обыкновенных дифференциальных уравнения вида
|
|
|
|
ak 2 |
0 ; |
|
(3.44) |
r |
1 |
r k 2 |
r 0 . |
|
(3.45) |
||
|
|
|
|
||||
|
r |
|
|||||
|
|
|
|
|
|
||
Из предыдущего параграфа известно, |
что |
уравнение |
|||||
(3.44) имеет решение: |
|
|
|
|
|
|
|
|
|
|
|
C1e |
k 2 . |
|
(а) |
Уравнение (3.45) есть уравнение Бесселя, общий инте- |
|||||||
грал которого имеет вид: |
|
|
|
|
|
|
|
r C2 J 0 kr C3 Y0 kr , |
|
(б) |
|||||
где С1 и С2 . постоянные интегрирования, J0 |
и Y0 |
. Бесселя |
|||||
первого и второго рода нулевого порядка. Так как температура на оси цилиндра (r = 0) должна быть конечной величиной, а Y0(0) 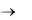 , то из физических соображений частное решение уравнения (3.45) не должно содержать бесселеву функцию второго рода и С3 должно быть равно нулю.
, то из физических соображений частное решение уравнения (3.45) не должно содержать бесселеву функцию второго рода и С3 должно быть равно нулю.
С учетом сказанного уравнение (б) принимает вид:
|
r C2 J 0 |
kr . |
|
(в) |
|||||
Если обозначить kr0 = , тогда частное решение уравне- |
|||||||||
ния (3.43) будет иметь вид: |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
r |
|
|
|
|
|
|
r 2 |
|
|
|
|||
r, |
Ce |
|
0 J 0 |
|
|
|
. |
(в) |
|
|
|
r0 |
|||||||
|
|
|
|
|
|
|
|
||
198
