
Методическое пособие 699
.pdf
стину жидкости при x . равна tж0. Температуры tc2 и tж0 известны. Задан удельный массовый расход охлаждающей жидкости G, кг/(м2 c), теплоемкость срж и теплопроводность ж которой постоянны. Необходимо найти распределение температуры в такой пористой стенке.
Будем рассматривать пористость пластины p как отношение объема пор ко всему объему материала. Для равномерной пористости можно считать, что на единице поверхности, нормальной к направлению потока жидкости, сечение для прохода жидкости fж = 0, а сечение твердого скелета, участвующего в теплопроводности, равно fc = 1 – fж = 1 . p. Отметим также, что если удельный массовый расход натекающей жидкости равен G, то массовый расход внутри пластины будет равен G/р.
Процесс переноса теплоты в таком пористом теле можно представить как теплопроводность самой пластины и теплообмен между твердым телом и жидкостью, протекающей через поры пластины.
Плотность теплового потока за счет теплопроводности самой пластины в сечениях х и х + dx запишется:
|
q x |
|
|
|
dt |
1 |
p |
|
|
|
c |
|
dx |
||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
q x dx |
|
d |
|
t |
|
dt |
dx 1 p . |
|
c |
dx |
|
|
dx |
||||
|
|
|
|
|
|
|
||
В условиях стационарного режима изменение теплового потока на участке dx произойдет вследствие теплообмена между твердым телом и протекающей через поры жидкостью, т. е.
dq qx qx dx Gcрж dt
или
|
dt |
1 p |
|
dt |
1 p |
|
|
d 2 t |
dx Gcрж dt . |
c dx |
c dx |
c dt 2 |
1 p |
||||||
Следовательно, для области 0 x |
дифференциальное |
||||||||
198
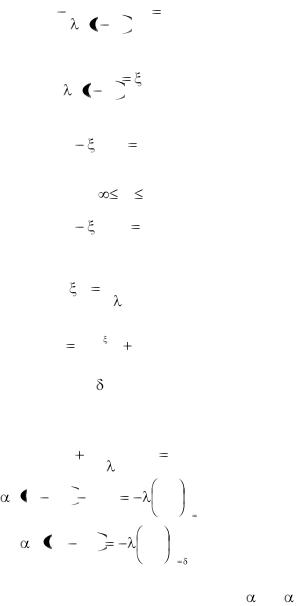
уравнение запишется: |
|
|
|
|
|
|
|
|
|
d 2 t |
|
Gcрж |
|
|
dt |
0 . |
(а) |
|
dx 2 |
|
c 1 |
p dx |
||||
|
|
|
|
|||||
Если обозначить
Gcрж |
|
, |
|
|
c |
||
c 1 p |
|||
|
|
то соотношение (а) запишется:
|
|
d2 t |
|
|
|
dt |
|
|
0 . |
|
|
|
|
|
|
(2.121) |
||||
|
|
dx 2 |
|
c |
|
dx |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Аналогичным образом можно получить дифференциаль- |
||||||||||||||||||||
ное уравнение и для области . |
|
|
x |
|
0: |
|
|
|
|
|
|
|||||||||
|
|
d 2 t |
|
|
|
|
dt |
|
|
0 , |
|
|
|
|
|
(2.122) |
||||
|
|
dx 2 |
|
ж dx |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gcрж |
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
ж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ж |
|
|
|
|
|
|
|
|
|
|
|
||
Общее решен уравнения (2.121) имеет вид: |
|
|||||||||||||||||||
|
|
t |
C1e c x |
C2 . |
|
|
|
|
|
|
||||||||||
Постоянные С1 |
и С2 определяются из граничных усло- |
|||||||||||||||||||
вий: при х = 0 t = tc1 и при х = |
|
|
|
|
t = tc2. |
|
|
|
||||||||||||
Уравнения теплопроводности и граничные условия име- |
||||||||||||||||||||
ют вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 t |
|
G ж cрж |
|
dt |
|
0 |
; |
|
(2.127) |
|||||||||
|
|
dx 2 |
|
|
|
|
|
|
|
|
dx |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
г t г |
|
t c1 |
|
G |
ж r |
|
|
|
|
|
dt |
|
; |
(2.128) |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
dx |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|||
|
|
t c2 |
t ж |
|
|
|
|
|
|
|
|
dt |
|
|
|
, |
|
(2.129) |
||
ж |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
dx x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
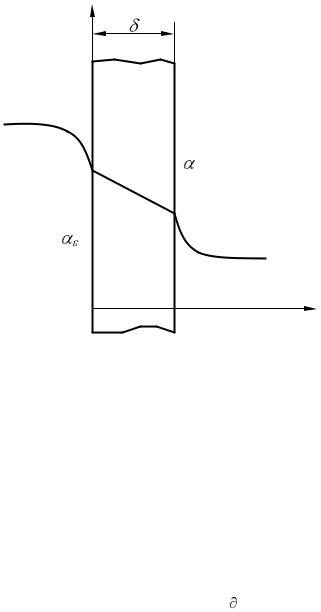
где (кроме обозначений, указанных на рис. 2.23); r – теплота парообразования; срж — теплоемкость жидкости; г и ж — коэффициенты теплоотдачи на поверхностях стенки, обра-
198
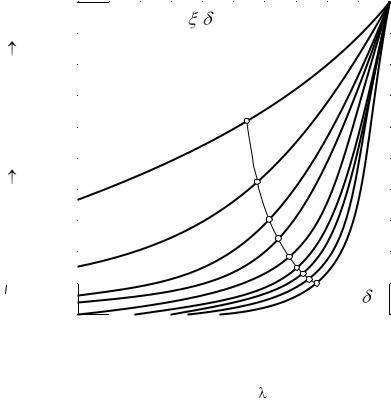
щенных соответственно к газу и жидкости. |
|
|
|||||
|
1,0 |
|
|
= 0 |
|
|
|
|
|
|
0 |
|
|
|
|
) |
0,8 |
|
|
|
|
|
|
ж0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– t |
|
|
|
|
|
|
|
с2 |
|
|
|
|
|
|
|
).(t |
0,6 |
|
|
|
|
|
|
ж |
|
|
|
|
|
|
|
– t |
|
|
1 |
|
|
|
|
(t |
|
|
|
|
|
|
|
) |
0,4 |
|
|
|
|
|
|
ж0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
t |
|
|
|
|
|
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с2 |
|
|
|
|
|
|
|
).(t |
|
|
|
|
|
|
|
ж |
|
|
|
|
|
|
|
– t |
|
|
3 |
4 |
5 |
|
|
(t |
|
|
|
|
|
|
x/ |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
0 |
0,2 |
0,4 |
|
0,6 |
0,8 |
1,0 |
|
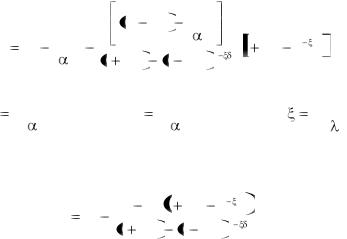
Рис. 2.22 Распределение температуры и средняя температура |
||||||
|
|
|
в пористой пластине |
|
|
||
Коэффициент теплопроводности в уравнении (2.127) в общем случае должен учитывать теплопроводность твердого скелета стенки и охлаждающей жидкости. Для металлических пористых стенок, имеющих высокий коэффициент теплопроводности и малый суммарный объем пор, теплопроводностью жидкости можно пренебречь. В этом случае, как и в предыдущей задаче, можно принимать .
Опустив промежуточные выкладки, приведем окончательное решение уравнения (2.127) при граничных условиях
(2.128) и (2.129):
198
|
|
|
|
|
|
|
t г |
t |
|
G ж r |
|
|
|
|
|
|
|
|
|
|
|
G |
ж r |
|
ж |
|
|
|
|
|
|
|
|
||||
t |
t |
|
|
|
|
|
|
г |
1 k |
|
e |
x |
, (2.130) |
|||||
г |
|
|
|
1 k г |
|
1 k ж e |
г |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
г |
|
|
|
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k г |
G ж cрж |
; |
|
|
k ж |
|
G ж cрж |
; |
|
|
|
|
Gж cрж |
. |
||||
|
г |
|
|
|
ж |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если охлаждение пористой стенки осуществляется без испарения охлаждающей жидкости, т. е. r = 0, то уравнение (2.130) принимает вид:
|
|
t г |
t ж 1 |
k г |
e |
x |
|
|
t t |
г |
|
|
|
|
|
. |
(2.131) |
|
k г |
|
k ж |
|
||||
|
|
1 |
1 |
e |
|
|||
2.13 Теплопроводность при наличии внутренних источников теплоты
В рассмотренных ранее задачах внутренние источники теплоты отсутствовали.
Однако в ряде случке внутри объектов исследования могут протекать процессы, в результате которых будет выделяться или поглощаться теплота. Примерами таких процессов могут служить: выделение джоулевой теплоты при прохождении электрического тока по проводникам; объемное выделение теплоты в тепловыделяющих элементах атомных реакторов вследствие торможения осколков деления ядер атомного горючего, а также замедления потока нейтронов; выделение или поглощение теплоты при протекании ряда химических реакций и т. д.
198
t
t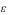
ж
tc1
tc2
tж
x
0
Рис. 2.23 Пористое охлаждение пластины (граничные условия третьего рода)
При исследовании переноса теплоты в таких случаях важно знать интенсивность объемного выделения (поглощения) теплоты, которая количественно характеризуется мощностью внутренних источников теплоты qv, Вт/м3. Если величина qv положительна, то говорят, что в теле имеются положительные источники теплоты. При отрицательных значениях qv имеются отрицательные источники (стоки) теплоты.
В зависимости от особенностей изменения величины в пространстве можно говорить о точечных, линейных, поверхностных и объемных источниках теплоты.
Для стационарного режима при t/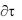 = 0 дифференциальное уравнение теплопроводности (1.24) при наличии источников теплоты имеет вид:
= 0 дифференциальное уравнение теплопроводности (1.24) при наличии источников теплоты имеет вид:
198
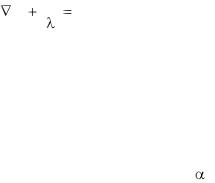
2 t |
q v |
0 . |
(2.132) |
|
а) Теплопроводность однородной пластины
Рассмотрим длинную пластину, толщина которой 2 — величина малая по сравнению с двумя другими размерами.
— величина малая по сравнению с двумя другими размерами.
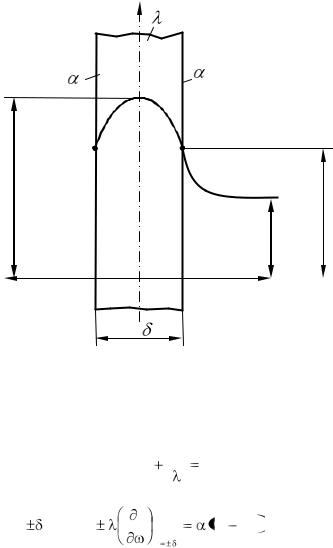
Источники теплоты равномерно распределены по объему и равны qv = const. Заданы коэффициенты теплоотдачи 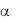 и температура жидкости вдали от пластины tж, причем = const и tж = const. Благодаря равномерному охлаждению температуры обеих поверхностей пластины одинаковы. При указанных условиях температура пластины будет изменяться только вдоль оси х, направленной нормально к поверхности тела. Температуры на оси пластины и на ее поверхности обозначим соответственно через t0 и tc; эти температуры неизвестны (рис. 2.24). Кроме того, необходимо найти распределение температуры в пластине и количество теплоты, отданное в окружающую среду.
и температура жидкости вдали от пластины tж, причем = const и tж = const. Благодаря равномерному охлаждению температуры обеих поверхностей пластины одинаковы. При указанных условиях температура пластины будет изменяться только вдоль оси х, направленной нормально к поверхности тела. Температуры на оси пластины и на ее поверхности обозначим соответственно через t0 и tc; эти температуры неизвестны (рис. 2.24). Кроме того, необходимо найти распределение температуры в пластине и количество теплоты, отданное в окружающую среду.
198
t = const
tж
t0
|
tж |
|
|
|
c |
|
|
t |
|
ж |
|
|
t |
|
- x |
+ x |
|
|
0 |
|
|
|
|
|
2 |
|
Рис. 2.24 Теплопроводность плоской пластины при наличии внутренних источников теплоты
Дифференциальное уравнение (2.132) в рассматриваемом случае упрощается и принимает вид:
|
|
d2 t |
|
q v |
0 . |
(2.133) |
|
|
dx 2 |
|
|
||||
|
|
|
|
|
|||
Граничные условия: |
|
|
|
|
|
|
|
при x = имеем |
|
t |
|
|
t c |
t ж . |
|
|
|
|
|
|
|||
|
|
|
|
|
|||
x
Поскольку граничные условия для обеих сторон пластины одинаковы, температурное поле внутри пластины должно быть симметричным относительно плоскости х = 0. Теплота с одинаковой интенсивностью отводится через левую и правую поверхности тела. Одинаково и тепловыделение в обеих половинах пластины. Это означает, что можно далее рассматривать
198
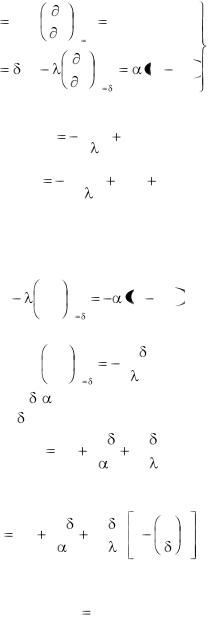
лишь одну половину пластины, например правую (рис. 2.24), и записать граничные условия для нее в виде
x |
0; |
t |
|
0; |
|||
|
|
|
|
||||
x x |
0 |
||||||
|
|
(2.134) |
|||||
x |
; |
|
|
t |
|
t c t ж . |
|
|
|
|
|
||||
|
|
x |
|
||||
|
|
|
|
|
x |
||
После интегрирования (2.133) получим:
dt |
|
q v x |
C1 |
; |
(2.135) |
dx |
|
|
|||
|
|
|
|
|
|
q |
x 2 |
|
|
||
t |
v |
|
C1x C |
2 . |
(2.136) |
|
2 |
||||||
|
|
|
|
|||
Постоянные интегрирования С1 и С2 определяются из граничных условий (2.134).
При х = 0 из уравнения (2.135) получаем С1 = 0; при х = 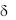 получаем:
получаем:
|
|
dt |
|
|
|
|
|
|
t c |
t ж . |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
dx |
|
x |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Из (2.135) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
q v |
. |
|
|
|
|
|
|
||||
|
|
|
dx |
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тогда tc = tж + qv / |
|
; подставив это выражение в уравне- |
||||||||||||||||||
ние (2.136), при х = |
получим: |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
q v |
|
|
|
q v |
2 |
|
|
|
|
|
||
|
C2 |
|
t |
|
|
|
|
|
|
|
. |
|
|
|
||||||
|
|
ж |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставив значения постоянных С1 и С2 |
в выражение |
|||||||||||||||||||
(2.136), найдем уравнение температурного поля: |
|
|||||||||||||||||||
|
|
|
q v |
2 |
|
|
|
|
|
x |
|
2 |
|
|
||||||
t z |
t ж |
|
|
|
|
q v |
|
1 |
|
|
|
. |
(2.137) |
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В рассматриваемой задаче тепловой поток изменяется вдоль оси х:
q q v x .
198

При х = 0 и q = 0 (это следует из условия: при х = 0 имеем (dt/dx)x = 0 = 0) Тепловой поток с единицы поверхности пластины при x = 
q t c t ж |
q v , |
(2.138) |
и общее количество теплоты, отданное всей поверхностью в единицу времени (вся поверхность F равна двум боковым поверхностям F1)
Q qF q v 2F1 |
(2.139) |
Из уравнения (2.137) следует, что температура в плоской стенке в случае симметричной задачи распределяется по параболическому закону.
Если в уравнении (2.137) положить  , то полученное выражение будет представлять температурное поле для граничных условий первого рода, ибо при
, то полученное выражение будет представлять температурное поле для граничных условий первого рода, ибо при 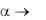 получим tж
получим tж 
tс.
С учетом сказанного уравнение (2.137) принимает вид:
t t |
|
q v 2 |
x 2 . |
(2.140) |
|
c |
2 |
|
|||
|
|
|
|
||
|
|
|
|
|
|
При этом температура на оси симметрии пластины (х =
0)
|
q v |
2 |
|
t 0 t c |
|
. |
|
2 |
|
||
|
|
|
а перепад температур между осью симметрии стенки и ее поверхностью
t 0 |
t c |
q v 2 |
q |
. |
(2.141) |
|
2 |
|
2 |
||||
|
|
|
|
|
||
До сих пор мы полагали, что коэффициент теплопроводности материала стенки постоянен. При больших перепадах температур может возникнуть необходимость в учете зависимости коэффициента теплопроводности от температуры. Часто эта зависимость имеет линейный характер:
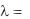 0 1 bt .
0 1 bt .
Тогда
198

q v x |
0 1 bt |
dt |
. |
(а) |
|
||||
|
|
dx |
|
|
Разделяя переменные и интегрируя последнее уравнение, получаем:
|
t 2 |
|
|
1 q v x 2 |
|
|||||||
t b |
|
|
|
|
|
|
|
|
|
C . |
(б) |
|
2 |
|
|
|
0 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
При х = 0 имеем t = t0, в этом случае из уравнения (б) |
||||||||||||
следует: |
|
|
|
|
|
|
|
|
|
|
|
|
|
C t |
|
|
|
b |
t |
2 |
. |
|
|
||
|
0 |
2 |
0 |
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
Подставляя найденное значение С в выражение (6) и решая квадратное уравнение относительно t, получаем следующее уравнение температурной кривой:
б) Теплопроводность однородного цилиндрического стержня
Рассмотрим круглый цилиндр (рис. 2.25), радиус которого мал по сравнению с длиной цилиндра. При этих условиях температура будет изменяться только вдоль радиуса.
Внутренние источники теплоты равномерно распределены по объему тел Заданы температура окружающей среды tж = const и постоянный по всей поверхности коэффициент теплоотдачи. При этих условиях температура во всех точках внешней поверхности цилиндра будет одинакова.
Для цилиндра, как и для пластины, задача будет одномерной и симметричной. Уравнение (2.132) при этом имеет вид:
d 2 t |
1 dt |
|
q v |
0. |
(2.143) |
|||
|
|
|
|
|
|
|
||
dr 2 |
|
r dr |
|
|
||||
|
|
|
|
|
||||
Граничные условия:
198
