
Методическое пособие 699
.pdf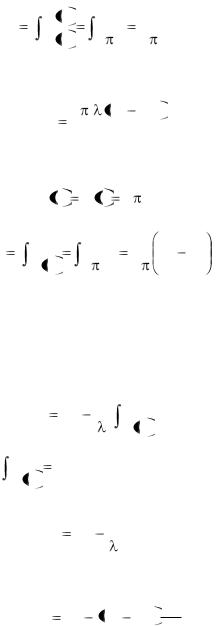
|
n 2 |
d n |
r2 |
|
In 2 |
|
|
|
|
|
|
|
||
n |
n |
|
F n |
r |
|
1 |
|
|
|
|
|
1 |
|
1 |
dr |
1 |
ln |
r2 |
. |
|
|
|
|
|
||
2 rl |
|
2 l |
|
r1 |
|
С учетом полученного значения |
I n 2 |
выражение (2.68) |
|||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
1 |
|
принимает вид: |
|
|
|
|
|
|
|
Q |
2 l |
t c1 |
t c2 |
. |
(2.70) |
||
|
ln |
r2 |
|
|
|||
|
|
|
|
|
|
||
|
|
r1 |
|
|
|
||
|
|
|
|
|
|
||
в) Для шаровой стенки n = r, n1 = r1 |
и n2 = r2, а |
||||||
F n |
F r |
4 |
r 2 , |
|
|
||
тогда
n 2
In 2
n1
n1
dn |
r2 |
dr |
1 |
1 |
1 |
|||
|
||||||||
|
|
|
|
|
|
|
|
|
F n |
r |
4 r 2 |
4 |
|
r |
|
r |
|
|
|
|
|
1 |
2 |
|||
|
1 |
|
|
|
|
|
|
|
и формула (2-68) применительно к шаровой стенке принимает вид:
Интегрируя выражение (2.67) в пределах от n1 до любой текущей координаты и в интервале температур от tc1 до t, получаем уравнение для температурного поля:
n 2
Обозначая
n1
сать:
|
t t c1 |
Q n |
dn |
. |
|||
|
|
n |
1 |
F n |
|||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
dn |
I n |
, последнее уравнение можно запи- |
|||||
|
|||||||
|
|||||||
|
n |
|
|
|
|
|
|
F n |
1 |
t t |
|
Q |
I |
n |
. |
|
c1 |
n |
|||||
|
|
1 |
||||
|
|
|
|
|
||
Подставляя в полученное выражение значение теплового потока Q из (2.68), получаем:
I n
t t c1 t c1 t c2 nn1 . (2.72)
I n 2
1
198

In
Отношение n1 в уравнении (2.72) можно рассматривать
In 2
n1
как некоторую приведенную безразмерную координату Х, которая зависит от геометрической формы стенки. Уравнение (2.72) можно привести к безразмерному виду:
|
|
|
|
|
|
t |
t |
c2 |
|
|
|
I nn |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
. |
(2.73) |
||
|
|
|
|
|
t c1 |
|
t c2 |
|
I nn 2 |
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
С обозначениями |
|
t |
|
t c2 |
|
|
(безразмерная температу- |
|||||||
|
|
t c1 |
|
t c2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ра) и |
|
I nn |
X |
уравнение (2.73) принимает вид: |
|
||||||||||
1 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
I n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
X . |
|
(2.73 ) |
|
|
Уравнение (2-73) является |
обобщенным |
выражением |
||||||||||||
температурного поля в безразмерных величинах для всех трех геометрических форм.
Приведенная безразмерная координата в уравнении (2.73 ) вычисляется с учетом геометрической формы стенки:
для плоской стенки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
XП |
x |
; |
|
|
(2.74) |
|||||||||
|
|
|
|
|
|
|||||||||||||
для цилиндрической стенки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln |
|
|
r |
|
|
|
|
|
|
|
|
||||
X |
X |
|
|
r1 |
; |
|
|
|
|
|
|
(2.75) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
Ц |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|||||
для шаровой стенки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X |
X Ш |
|
|
|
|
d1 |
|
d |
|
. |
(2.76) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
d1 |
d 2 |
|
|
|
|||||||||
198

Уравнения (2.68) и (2.73 ) получены при постоянном коэффициенте теплопроводности стенки. Аналог образом можно получить обобщенные зависимости и для случая, когда коэффициент теплопроводности является функцией температуры.
2.6 Пути интенсификации теплопередачи
а) Интенсификация теплопередачи путем увеличения коэффициентов теплоотдачи
Из уравнения теплопередачи
Q kF t
следует, что при заданных размерах стенки и температурах жидкостей величиной, определяющей теплопередачу, является k. Но поскольку теплопередача — явление сложное, то правильное решение можно найти только на основе анализа частных составляющих, характеризующих процесс. Так, например, если мы имеем дело с плоской стенкой, для которой
|
|
|
k |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||
то при |
0 (что можно принять для тонких стенок с боль- |
||||||||||||||||||||||||||
шим коэффициентом |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
k |
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
. |
(2.77) |
||
|
|
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
2 |
|
|
2 |
|
|
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Из уравнения (2.77) следует, что коэффициент теплопе- |
|||||||||||||||||||||||||||
редачи не может быть больше самого малого . При |
1 |
||||||||||||||||||||||||||
коэффициент теплопередачи стремится к |
2. |
|
|
|
|||||||||||||||||||||||
Проследим это на числовых примерах. |
|
|
|
||||||||||||||||||||||||
а) 1) |
1 = 40 и |
2 =5000 Вт/(м2 К); |
|
|
|
|
|
||||||||||||||||||||
2) 1 = 40 и 2 =10000 Вт/(м2 К); |
|
|
|
|
|
||||||||||||||||||||||
198

По формуле (2.77) находим, что коэффициенты теплопе-
редачи будут равны: |
|
||
k1 |
39,7 Вт/(м2 К) и k 2 |
39,8 Вт/(м2 К) |
|
б) 1) |
1 = 80 и |
2 =5000 Вт/(м2 К); |
|
2) 1 = 200 и |
2 =5000 Вт/(м2 К); |
||
Для случая (б) находим, что коэффициенты теплопереда- |
|||
чи становятся равными: |
|
||
k1 |
78,8 Вт/(м2 К) и k 2 |
192 Вт/(м2 К) |
|
б) Интенсификация теплопередачи за счет оребрения |
|||
стенок |
|
|
|
При передаче теплоты через цилиндрическую стенку |
|||
термические сопротивления l/ |
1d1 и l/ 2d2 определяются не |
||
только значениями коэффициентов теплоотдачи, но и размерами самих поверхностей. При передаче тепла через шаровую стенку влияние диаметров d1 и d2 оказывается еще сильнее, что видно из соотношений l/ 1d12 и l/ 2d22. Отсюда следует, что если мало, то термическое сопротивление теплоотдачи можно уменьшить путем увеличения соответствующей поверхности. Такой же результат можно получить и для плоской стенки, если одну из поверхностей увеличить путем оребрения. Последнее обстоятельство и положено в основу интенсификации теплопередачи за счет оребрения. При этом термические сопротивления станут пропорциональными величинами
1 |
и |
1 |
. |
|
|
||
1F1 |
2 F2 |
Следует указать, что при использовании метода оребрения нужно руководствоваться следующими соображениями: если 1 << 2, то оребрять поверхность со стороны 1 следует до тех пор, пока 1F1 не достигает значения 2F2. Дальнейшее увеличение поверхности F1 малоэффективно. Ребристые поверхности изготавливаются или в виде сплошных отливок или отдельных ребер, прикрепленных к поверхности.
198
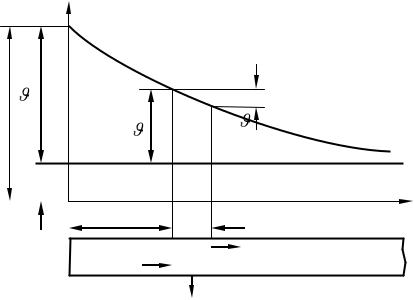
Строгое аналитическое решение задачи о распространения тепла в ребре связано со значительными трудностями. В основу решения поэтому кладут некоторые допущения, которые позволяют сравнительно простым путем получить нужный результат. Ниже рассмотрим метод решения задач о теплопроводности в ребрах простейших геометрических форм.
2.7 Теплопроводность в стержне (ребре) постоянного поперечного сечения
а) Дифференциальное уравнение его решения.
Ребра в поперечном сечении могут иметь профиль самой различной геометрической конфигурации (прямоугольник, круг, треугольник и другие фигуры, в том числе и неправильной геометрической формы).
t
1 |
d |
tж |
|
x |
|
|
|
|
|
|
|
dx |
|
|
|
||
|
Qx |
|
Qx+ |
|
|
||
|
|
|
|
|
|
d |
|
|
|
||
Рис. 2-12 Перенос теплоты через стержень
198

Рассмотрим распространение тепла прямом стержне с постоянным поперечным сечением по длине. Обозначим площадь поперечного сечения стержня через f и периметр через u. Стержень находится в среде с постоянной температурой tж, коэффициент теплоотдачи от поверхности стержня к окружающей среде будем считать постоянным для всех поверхности. Будем полагать также, что коэффициент теплопроводности материала стержня достаточно велик, а поперечное сечение очень мало по сравнению с его длиной. Последнее дает основание пренебречь изменением температуры в поперечном сечении и считать, что она изменяется только вдоль оси стержня. Для удобства дальнейших выкладок отсчет температуры будем вести от tж = const. Отсчитанную таким образом избыточную температуру стержня обозначим через . Очевидно,
t t ж ,
где tж – температура среды, окружающей стержень; t – текущая температура стержня.
Если задана температура основания стержня t1 то избыточная температура стержня (рис. 2.12) будет:
1 t1 t ж .
На расстоянии х от основания стержня выделим элемент стержня длиной dx. Уравнение теплового баланса для рассматриваемого элемента можно записать:
Q x 
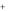 dQ , (а)
dQ , (а)
где Qx – количество теплоты, входящее в левую грань элемента за единицу времени; Qx+dx - количество теплоты, которое выходит из противоположной грани элемента за то же время; dQ – количество теплоты, отдаваемое за единицу времени наружной поверхностью элемента окружающей его среде.
Согласно закону Фурье |
|
|
|
Qx |
d |
f |
|
dx |
|||
|
|
||
и |
|
|
198

Qx |
|
|
d |
|
d |
|
dx f , |
|||
dx |
|
|
|
|
|
|
|
|||
dx |
|
|
|
|||||||
|
|
|
dx |
|
||||||
откуда |
|
|
|
|
|
|
|
|
|
|
Q x |
|
f |
|
d |
f |
d 2 |
dx . |
|||
dx |
|
dx |
dx 2 |
|||||||
|
|
|
|
|
|
|
||||
Следовательно,
Qx Qx dx f |
d 2 |
dx . |
|
dx 2 |
|||
|
|
С другой стороны, согласно закону Ньютона-Рихмана: dQ 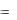 p udx .
p udx .
(б)
(в)
Приравнивая (б) и (в) получаем следующее дифференциальное уравнение, описывающее изменение температуры стержня:
|
d 2 |
|
p u |
|
|
m2 |
, |
(2.78) |
|
|
dx 2 |
f |
|
||||||
|
|
|
|
|
|||||
где |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
p u |
; |
|
(г) |
||
|
|
|
|
|
|||||
|
|
|
f |
|
|||||
величина m измеряется в 1/м.
Из выражения (г) видно, что для ребра, форма и размеры которого заданы, при условии постоянства коэффициента теплоотдачи p по всей поверхности и постоянства коэффициента в рассматриваемом интервале температур, величина m = const. Тогда общий интеграл для уравнения (2.78) будет:
C1e mx C2 e mx . |
(2.79) |
Значения постоянных С1 и С2 определяются из граничных условий. Граничные условия могут быть заданы поразному в зависимости от длинны стержня и других факторов.
б) Стержень бесконечной длины
В начальном сечении стержня температура поддерживается постоянной, т. е. при х = 0 величина = 1. Если длина
198
стержня l |
, то вся теплота, подводимая к стержню, будет |
|
отдана им в окружающую среду и при x |
имеем = 0. |
|
Подстановка граничных условий в уравнение (2.79) дает: |
||
при x = 0 |
1 = C1 + C2; |
|
при x |
C1e = 0. |
|
Последнее равенство возможно только при С1 = 0. Таким |
||
образом, С2 = |
1. Подставляя эти значения постоянных С1 и С2 |
|
в уравнение (2-79) получаем: |
|
|
|
1e mx . |
(2.80) |
Последнее равенство можно записать в виде:
e mx , |
(2.80 ) |
1
где - безразмерная температура, выраженная в долях температуры 1 начального сечения стержня.
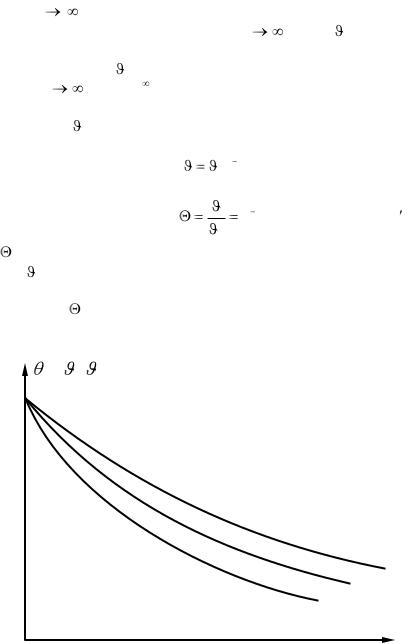
На рис. 2.13 представлена зависимость безразмерной температуры от длины стержня при различных значениях параметра m (m1 < m2 < m3).
= / 1
1
m1
m2
m3
x
0
Рис. 2.1 Изменение температуры по длине стержня
198

Из рассмотрения рис. 2.13 следует, что безразмерная температура убывает тем сильнее, чем больше множитель m.
При x |
все кривые асимптотически приближаются к = 0. |
||
|
|
|
|
Из |
уравнения m |
p u / f следует, что величина m |
|
пропорциональна теплоотдаче с боковой поверхности и обрат-
но пропорциональна 
 f . фактору, определяющему передачу теплоты теплопроводностью вдоль стержня. Отсюда следует, что при оребрении нужно выбирать материал для ребер с большим коэффициентом теплопроводности. Последнее приводит к уменьшению m и сохранению больших избыточных температур вдоль стержня. При p / = const величина m возрастает с возрастанием u/f, что указывает на более эффективную работу ребер с профилями, имеющими меньшее отношение u/f при том же поперечном сечении.
f . фактору, определяющему передачу теплоты теплопроводностью вдоль стержня. Отсюда следует, что при оребрении нужно выбирать материал для ребер с большим коэффициентом теплопроводности. Последнее приводит к уменьшению m и сохранению больших избыточных температур вдоль стержня. При p / = const величина m возрастает с возрастанием u/f, что указывает на более эффективную работу ребер с профилями, имеющими меньшее отношение u/f при том же поперечном сечении.
Количество теплоты, передаваемое стержнем окружающую среду, очевидно, будет равняться количеству теплоты, проходящему через его основание.
Через основание стержня проходит тепловой поток
Q |
d |
f ; |
|
|
|||
dx |
|||
|
x 0 |
здесь Q измеряется в ваттах.
Из уравнения (2.80) находим:
d |
me mx |
1 |
|
x 0 |
m 1 . |
|
|||||
|
|
||||
dx |
|
||||
x 0 |
|
|
|
|
Подставляя значение градиента температуры при x = 0 в предыдущее уравнение для теплового потока, получаем формулу, определяющую количество теплоты, отданное стержнем в окружающую среду:
|
|
|
|
Q fm 1 1 p uf . |
(2.81) |
||
в) Стержень конечной длины
Для стержня конечной длины дифференциальное урав-
198
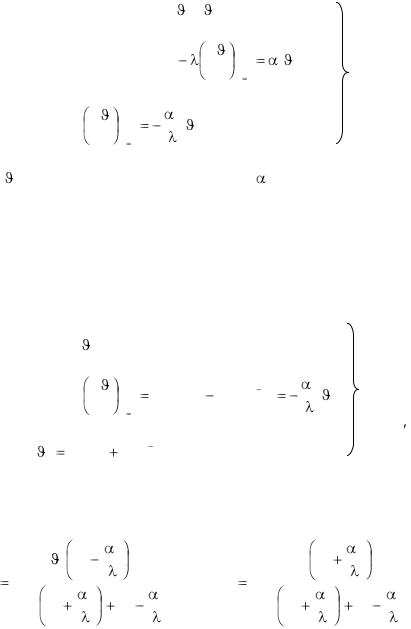
нение (2.78) и его решение (2.79) сохраняет силу, но граничные условия будут другими:
при |
x = 0 |
= |
1; |
|
|||||
при |
x = l |
|
|
|
|
d |
l l ; |
||
|
|
|
|
|
|||||
|
|
|
|
dx |
|||||
|
|
|
|
|
|
|
|
x l |
|
|
|
|
|
|
|
|
|
|
(2.82) |
или |
|
d |
|
|
1 |
|
, |
|
|
|
dx |
|
|
l |
|
|
|||
|
|
x l |
|
|
|
||||
где l – температура на конце стержня; l – коэффициент теплоотдачи с торца стержня.
При х = 1 имеет место равенство количества теплоты, подведенного к торцу стержня за счет теплопроводности и количества теплоты, отдаваемого поверхностью торца в окружающую среду за счет теплоотдачи. Для определения постоянных С1 и С2 в уравнении (2.79) используем граничные усло-
вия (2.82):
при |
x = 0 |
1 = C1 + C2; |
|
|
|
|
|
|||
при |
x = l |
|
d |
C |
|
meml |
C |
me ml |
l |
|
|
|
|
||||||||
|
|
1 |
|
l |
||||||
|
|
|
dx |
|
|
2 |
|
|
||
|
|
|
x l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.82 ) |
|
и |
l |
C1eml |
C2 e ml . |
|
|
|
|
|||
Из полученных уравнений (2.82) определяем постоянные С1 и С2:
|
|
m |
l |
|
e2ml |
m |
l |
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
; |
C2 |
|
|
|
|
. |
||||||
e2ml m |
|
|
|
|
|
|
e2ml m |
|
|
|
||||||||
|
l |
|
m |
l |
|
|
|
l |
m |
l |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
198
