
Методическое пособие 699
.pdf
цу изотермической поверхности при температурном градиенте, равном единице.
Т.к. тела могут иметь различную температуру, а при наличии теплообмена и в самом теле температура будет распределена неравномерно, то в первую очередь важно знать зависимость коэффициента теплопроводности от температуры. Опытным путем получена следующая линейная зависимость:
0[1 b(t t0 )] , |
(1.14) |
где 0 – значение коэффициента теплопроводности при температуре t0; b – постоянная, определяемая опытным путем.
Коэффициент теплопроводности газов Согласно кинетической теории перенос теплоты тепло-
проводностью в газах при обычных давлениях и температурах определяется переносом кинетической энергии молекулярного движения в результате хаотического движения и столкновения отдельных молекул газа. Коэффициент теплопроводности определяется соотношением:
|
|
|
|
|
|
(1.15) |
|
|
|
|
lcv / 3 |
||
|
|
|
||||
где |
- средняя скорость перемещения молекул газа; l - сред- |
|||||
няя длина свободного пробега молекул газа между соударениями; c - теплоемкость газа при постоянном объеме; 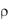 -
-
плотность газа.
С увеличением давления в равной мере увеличивается , уменьшается длина пробега l и произведение l сохраня-
ется постоянным. Поэтому коэффициент теплопроводности с изменением давления не изменяется.
Средняя скорость перемещения молекул газа зависит от температуры:
3R T
(1.16)
где R - универсальная газовая постоянная (8314,2 Дж/(кмольК); 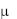 - молекулярная масса газа; Т– температура, К.
- молекулярная масса газа; Т– температура, К.
198
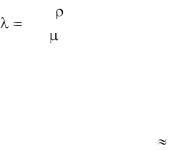
Коэффициент теплопроводности увеличивается с ростом температуры. Пределы изменения теплопроводности газов от 0.006 до 0.6 Вт/(мК).
Коэффициент теплопроводности жидкостей Механизм распространения теплоты в капельных жид-
костях можно представить как перенос энергии путем нестройных упругих колебаний. Была получена формула для коэффициента теплопроводности следующего вида:
|
cp |
4 / 3 |
|
|
A |
|
, |
(1.17) |
|
|
1/ 3 |
|||
|
|
|
|
где cp - теплоемкость жидкости при постоянном давлении; 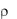 - объемная плотность жидкости;
- объемная плотность жидкости; 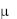 - относительная молекуляр-
- относительная молекуляр-
ная масса. Коэффициент А, пропорционален скорости распространения упругих волн в жидкости, не зависит от природы жидкости, но зависит от температуры, при этом Аср const.
Так как плотность жидкости с повышением температуры убывает, то из уравнения (1.17) следует, что для жидкостей с постоянной молекулярной массой с повышением температуры коэффициент теплопроводности должен уменьшатся.
Коэффициент теплопроводности твердых тел Металлы и сплавы. В металлах основным передатчиком
теплоты являются свободные электроны, которые подобны идеальному одноатомному газу. Передача теплоты при помощи колебательных движений атомов или в виде упругих звуковых волн не исключается, но бесконечно мала. Вследствие движения свободных электронов происходит выравнивание температуры во всех точках нагревающегося или охлаждающегося металла. Свободные электроны движутся как из областей с высокой температурой в области с более низкой, так и наоборот (отдают или принимают энергию). Так как в металлах носителем тепловой и электрической энергии являются электроны, то коэффициенты тепло – и электропроводности пропорциональны друг другу. При повышении температуры вследствие усиления тепловых неоднородностей рассеивание электронов увеличивается. Это приводит к уменьшению тепло
198

– и электропроводности чистых металлов. Для чистой меди =396 Вт/(мК), для той же меди с примесью мышьяка =142 Вт/(мК), это объясняется увеличением структурных неодно-
родностей, которые приводят к рассеиванию электронов. Твердые тела – диэлектрики (неметаллы). В диэлектри-
ках с повышением температуры коэффициент теплопроводности обычно увеличивается. Коэффициент теплопроводности зависит от структуры материалов их пористости и влажности. Многие строительные и теплоизоляционные материалы (кирпич, бетон, асбест, шлак и др.) нельзя рассматривать как сплошную среду из за наличия пор и закон Фурье в данном случае не действует.
Коэффициент теплопроводности порошкообразных и пористых тел сильно зависит от их объемной плотности (при возрастании плотности от 400 до 800 кг/м3 - асбеста увеличивается от 0.105 до 0.248 Вт/(мК)). Такое влияние плотности на коэффициент теплопроводности объясняется тем, что теплопроводность заполняющего поры воздуха значительно меньше, чем твердых компонентов.
Эффективный коэффициент теплопроводности пористых материалов сильно зависит от влажности. Для влажного материала коэффициент теплопроводности значительно выше (для сухого кирпича 0.35, для воды 0.6, для влажного кирпича 1Вт/(мК)). Это объясняется конвективным переносом теплоты, возникающим благодаря капиллярному движению воды внутри пористого материала и частично тем, что абсорбционно связанная влага имеет другие характеристики по сравнению со свободной водой.
Коэффициенты теплопроводности строительных и теплоизоляционных материалов имеют значения, лежащие примерно в пределах от 0.023 до 2.9 Вт/(мК). Материалы с 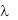 0.25Вт/(мК) обычно применяются для теплоизоляции и на-
0.25Вт/(мК) обычно применяются для теплоизоляции и на-
зываются теплоизоляционными.
198

1.5 Дифференциальное уравнение теплопроводности
Для того чтобы изучить физическое явление необходимо установить зависимость между величинами, характеризующими это явление. Для сложных физических процессов определяющие величины могут существенно изменятся в пространстве и времени – поэтому в исследованиях ограничивается промежуток времени и из всего пространства рассматривается элементарный объем, что позволяет существенно упростить зависимость. Таким образом, элементарный объем dv и элементарный промежуток времени d , это пределы в которых рассматривается изучаемый процесс. С математической точки зрения данные величины бесконечно малы, а с физической точки зрения достаточно велики чтобы рассматривать их как сплошную среду. Полученная зависимость является общим дифференциальным уравнением рассматриваемого процесса. Интегрируя дифференциальные уравнения, можно получить аналитическую зависимость между величинами для всей рассматриваемой области и промежутка времени.
Для решения задач, связанных с нахождением температурного поля, используют дифференциальное уравнение теплопроводности.
Для облегчения вывода диф. Уравнения используются следующие допущения:
-тело однородно и изотропно;
-физические параметры постоянны;
-деформация рассматриваемого объема, связанная с изменением температуры, является очень малой величиной по сравнению с самим объемом;
-внутренние источники теплоты в теле, которые в общем
случае могут быть заданны как qv f (x, y, z, ) , распре-
делены равномерно.
В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии, который в рассматриваемом случае формулируется следующим образом:
198
количество теплоты dQ , введенное в элементарный объем из-
вне за время d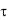 вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмотрения изохорического или изобарического процесса), содержащегося в элементарном объеме:
вследствие теплопроводности, а также от внутренних источников, равно изменению внутренней энергии или энтальпии вещества (в зависимости от рассмотрения изохорического или изобарического процесса), содержащегося в элементарном объеме:
dQ1 dQ2 dQ |
(1.18) |
где dQ1 - количество теплоты, Дж, введенное в элементарный объем путем теплопроводности за время d ; dQ2 - количество
теплоты, которое за время d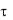 выделилось в элементарном объеме dv за счет внутренних источников энергии; dQ - изменение внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме dv , за время d .
выделилось в элементарном объеме dv за счет внутренних источников энергии; dQ - изменение внутренней энергии или энтальпии вещества, содержащегося в элементарном объеме dv , за время d .
Z |
dQz+d |
dQy |
|
|
|||
|
dQx |
|
dQx+d |
|
|
||
|
|
|
|
|
dz |
|
dy |
|
|
||
|
dQy+d |
dQz |
|
|
|
||
|
0 |
|
X |
|
|
|
|
Y |
|
|
|
|
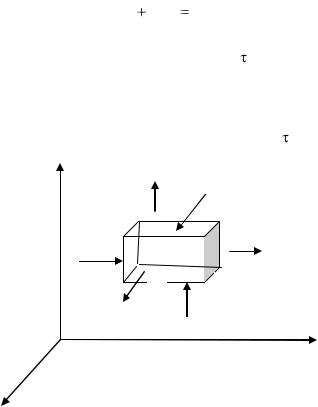
Рисунок 1.2 Схема элементарного объема |
||
Для нахождения составляющих уравнения (1.18) выделим в теле элементарный параллелепипед со сторонами dx,dy,dz (рис. 1.2). Параллелепипед расположен так, чтобы
его грани были параллельны соответствующим координатным плоскостям.
198

Количество теплоты, которое подводится к граням элементарного объема за время d в направлении осей Ox,Oy,Oz , обозначим соответственно dQX ,dQY ,dQZ .
в направлении осей Ox,Oy,Oz , обозначим соответственно dQX ,dQY ,dQZ .
Количество теплоты, которое будет отводиться через противоположные грани в тех же направлениях, обозначим
соответственно dQ X dX , dQ Y dY , dQ Z dZ . |
Количество теплоты, |
|
подведенное к грани |
dy, dz в направлении оси Ox за время |
|
d , составляет dQX |
qx dydzd , где q x |
- проекция плотности |
теплового потока на направление нормали к указанной грани. Количество теплоты, отведенное через противоположную грань элементарного параллелепипеда в направлении оси Ox , записывается в следующем виде:
(1.19)
Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него за время d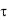 в направлении оси Ox , представляет собой количество теплоты
в направлении оси Ox , представляет собой количество теплоты
|
|
dQX1 |
|
dQX |
dQX dX |
|
|
|
(1.20) |
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dQ X1 |
qX dydzd |
|
|
qX dX dydzd |
(1.21) |
|||||||||||
Функция q X dX является непрерывной в рассматриваемом |
||||||||||||||||
интервале dx и может быть разложена в ряд Тейлора: |
|
|||||||||||||||
|
|
|
|
|
q |
X |
|
|
2q |
X |
|
dx 2 |
(1.22) |
|||
q |
|
q |
|
|
|
dx |
|
|
|
..... |
||||||
X dX |
X |
x |
x2 |
2! |
||||||||||||
|
|
|
|
|
|
|||||||||||
Если ограничится двумя первыми членами ряда, то |
||||||||||||||||
уравнение (1.21) запишется в виде |
|
|
|
|
|
|
||||||||||
|
|
dQ |
|
|
|
|
qX |
dxdydzd |
(1.23) |
|||||||
|
|
X1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Аналогичным образом можно найти количество теплоты, подводимое в направлениях двух других координат.
Количество теплоты подведенное теплопроводностью к рассматриваемому объему, будет равно:
198

dQ |
|
qX |
|
qY |
|
qZ |
dxdydzd |
(1.24) |
1 |
|
|
|
|
||||
|
x |
|
y |
|
z |
|
||
|
|
|
|
|
||||
Определим вторую составляющую уравнения (1.18). Обозначим количество теплоты, выделяемое внутренними источниками в единице объема среды в единицу времени и называемое мощностью внутренних источников теплоты, через q v ,
Вт/м3. Тогда
dQ 2 q v dvd |
(1.25) |
Третья составляющая в уравнении (1.18) находится в зависимости от характера термодинамического процесса изменения системы.
В случае рассмотрения изохорического (объем = const) процесса вся теплота, подведенная к элементарному объему, уйдет на изменение внутренней энергии вещества, заключен-
ного в этом объеме, т.е. dQ |
|
dU . |
|
|||
Если рассматривать внутреннюю энергию единицы |
||||||
объема u u(t, v) , тогда dU найдется как |
|
|||||
dU Cv |
|
t |
d dv cv |
t |
d dv, |
(1.26) |
|
|
|
||||
где C v - изохорная теплоемкость единицы объема, Дж/(м3К); cv - изохорная теплоемкость единицы массы, Дж/(кгК); 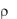 -
-
плотность вещества, кг/м3.
Подставим полученные выражения (1.24), (1.25) и (1.26) в уравнение (1.18), получим:
cv |
t |
|
|
qx |
|
qy |
|
qz |
qv |
, |
(1.25) |
|
|
|
|
|
x |
|
y |
|
z |
||||
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cv |
|
t |
divq |
qv , |
|
|
(1.26) |
|||
|
|
|
|
|
|
|||||||
|
|
|
|
|
||||||||
Выражение (1.26) является дифференциальным уравнением энергии для изохорического процесса переноса теплоты.
198
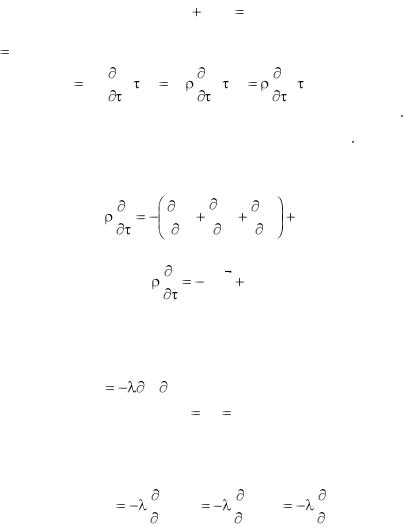
При рассмотрении изобарического процесса вся теплота, подведенная к объему, уйдет на изменение энтальпии вещества, заключенного в этом объеме, и уравнение (1.18) запишется следующим образом:
|
|
|
dQ1 dQ2 dI , |
|
|
(1.27) |
||
Если |
рассматривать энтальпию |
единицы |
объема, как |
|||||
i i(t, p) , то можно получать следующее выражение: |
||||||||
dI |
Cp |
t |
d dv cp |
t |
d dv |
i |
d dv , |
(1.28) |
|
|
|
||||||
где Cp - изобарная теплоемкость единицы объема, Дж/(м3 К); cp - изобарная теплоемкость единицы массы, Дж/(кг К).
Если полученные выражения (1.24), (1.25) и (1.28) подставить в уравнение (1.27), получим:
|
i |
|
|
qx |
|
qy |
|
qz |
qv |
, |
(1.29) |
|
|
|
|
|
|
x |
|
y |
|
z |
|||
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
divq |
qv . |
|
|
(1.30) |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||
Соотношение (1.30) является дифференциальным уравнением энергии в самом общем виде для изобарического процесса переноса теплоты.
В твердых телах перенос теплоты осуществляется по
закону Фурье q |
t / x, |
числовое значение разности cp и |
|||||||
сv мало и можно принять cv |
cp |
c . |
|
|
|
||||
Из уравнения (1.10) следует, что проекции вектора |
|||||||||
плотности теплового потока на координатные оси |
Ox,Oy,Oz |
||||||||
определяются выражениями: |
|
|
|
|
|
|
|||
qx |
|
t |
; qy |
t |
; qz |
t |
. |
(1.31) |
|
|
|
|
|
||||||
|
|
x |
|
y |
z |
|
|||
Подставляя полученные выражения (1.31) в уравнение
(1.26) получим:
198

|
t 1 |
|
t |
|
|
|
t |
|
|
|
t |
t |
t |
t |
|
qv |
, |
|||||||
|
|
|
c |
|
x |
|
|
|
x |
|
|
|
y |
|
y |
|
z |
|
z |
|
c |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
t |
|
|
1 |
|
div( |
gradt ) |
|
qv |
|
|
|
|
(1.32) |
||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
c |
|
|
|
|||||||
Выражения (1.32) называются дифференциальными уравнениями теплопроводности которые устанавливают связь между временным и пространственным изменением температуры в любой точке тела, в котором происходит процесс теплопроводности.
Дифференциальное уравнение теплопроводности в частных производных при постоянных теплофизических характеристиках имеет вид:
t |
|
2 t |
|
2 t |
|
2z |
|
q |
v |
(1.33) |
||
|
|
c |
|
x2 |
|
y2 |
|
z2 |
|
c |
|
|
|
|
|
|
|
|
|
|
|||||
В уравнении (1.33) принимаем следующие обозначения:
|
|
|
|
|
|
a , |
|
(1.34) |
|
|
|
c |
|
||||
|
|
|
|
|
|
|
||
2 t |
|
2 t |
|
|
2 t |
2 t , |
(1.35) |
|
x 2 |
|
y2 |
|
z2 |
||||
|
|
|
|
|||||
где - оператор Лапласа в декартовой системе координат записывается в следующем виде:
|
|
|
|
2 |
|
|
2 |
|
2 |
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(1.36) |
|
|
|
|
|
|
|
x 2 |
|
|
|
y2 |
|
z2 |
|
|
|||||||
Выражение |
2 t |
в цилиндрической системе координат |
|||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
2 t |
1 |
|
t |
1 |
|
2 t |
2 t |
, |
(1.37) |
|||||||||
|
|
r2 |
|
|
r |
|
|
r |
|
|
r2 |
|
2 |
|
|
|
z2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где r - радиус – вектор; |
- полярный угол; |
z |
- аппликата. |
||||||||||||||||||
Выражение |
2 t |
в сферических координатах имеет вид: |
|||||||||||||||||||
198

2 t |
2 t |
|
2 t |
1 |
|
1 2 |
|
t |
1 |
|
2 t |
, (1.38) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r2 |
|
r r |
|
r |
|
|
|
r2 (1 2 ) |
2 |
||||||||
|
|
|
|
|
|
|
|
||||||||||
где r - радиус – вектор; |
cos ; |
|
и |
- соответственно по- |
|||||||||||||
лярное расстояние и долгота.
С учетом сокращений уравнение (1.33) принимает следующий вид:
t |
a 2 t |
qv |
. |
(1.39) |
|
|
|||
|
|
c |
|
|
Коэффициент пропорциональности а, м2/с, в уравнении (1-39) называется коэффициентом температуропроводности и является физическим параметром вещества. Он существенен для нестационарных тепловых процессов и характеризует скорость изменения температуры.
Если имеются внутренние источники теплоты, но температурное поле соответствует стационарному состоянию, т.е. t=t(x,y,z), то дифференциальное уравнение теплопроводности превращается в уравнение Пуассона:
2 t |
|
2 t |
|
2 t |
|
q v |
0. |
(1.40) |
x 2 |
|
y2 |
|
z2 |
|
|
||
|
|
|
|
|
|
Наконец, для стационарной теплопроводности и отсутствия внутренних источников теплоты выражение (1.33) принимает вид уравнение Лапласа:
2 t |
|
2 t |
|
2 t |
0. |
(1.41) |
x 2 |
|
y2 |
|
z2 |
||
|
|
|
|
Нахождение частных решение этих уравнений в частных производных и некоторых других является основным содержанием теории теплопроводности.
1.6 Условия однозначности для процессов теплопроводности
Так как дифференциальное уравнение теплопроводности выведено на основе общих законов физики, то оно описывает явление теплопроводности в самом общем виде. Чтобы из
198
