
Методическое пособие 699
.pdf
Подставляя полученные значения С1 и С2 г уравнение (2.79), получаем:
|
emx m |
l |
|
|
|
e mx e2ml m |
|
l |
|||||||||
1 |
|
|
|
|
|
|
|
. (2.83) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2ml m |
l |
|
m |
l |
|
|
e2ml m |
l |
|
m |
l |
|
|
|||
|
|
|
|
||||||||||||||
Умножив и разделив правую часть уравнения (2.83) на e.ml и произведя простые алгебраические преобразования, получим:
|
|
|
|
m em(l x ) |
e m l x |
|
|
|
l |
em(l x ) e m l x |
|
||||||||
1 |
|
|
|
|
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
m eml e ml |
|
|
|
l |
eml |
e ml |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Напомним, что |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ex |
e x |
|
|
|
|
|
|
ex |
e x |
|
||||||||
|
|
|
|
|
|
|
ch x |
и |
|
|
|
|
|
|
|
sh x . |
|
||
2 |
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
С учетом сказанного уравнение (2.83) запишется: |
|
||||||||||||||||||
|
|
|
|
|
ch m l |
x |
|
l |
sh m l |
x |
|
||||||||
|
|
|
|
m |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(2.83 ) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
ch ml |
|
l |
sh ml |
|
|
|
|
|
||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если теплоотдачей с конца стержня пренебречь, то гра- |
|||||||||||||||||||
ничные условия (2.82) можно записать в виде |
|
||||||||||||||||||
при x = 0 |
= |
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
при x l |
|
d |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x l |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Последнее можно допустить, для случая, когда |
l на тор- |
||||||||||||||||||
це стержня мало, а коэффициент теплопроводности материала
велик и отношение l/ |
0 , т. е. можно пренебречь тепло- |
отдачей с торца стержня. |
|
Для этих условий в соотношении (2.83 ) вторые члены числителя и знаменателя правой части обращаются в нуль и
198

уравнение принимает вид: |
|
|
|
|
|
ch m l x |
; |
(2.84) |
|
1 |
ch ml |
|||
|
|
|||
|
|
|
здесь измеряется в °С.
По формулам (2.83 ) и (2.84) можно вычислить температуру в любом сечении стержня. Обычно доля теплоты, отдаваемой с торца стержня, является величиной малой по сравнению с количеством теплоты, отдаваемым с поверхности ребра, и для практических инженерных расчетов, как правило, используется формула (2.84).
В предельном случае, когда х = l, формула (2.84) принимает вид:
|
1 |
. |
|
x l |
ch ml |
||
|
|||
|
|
Количество теплоты Qp, Вт, отдаваемое поверхностью ребра в окружающую среду, будет равно количеству теплоты, подводимому к основанию ребра:
Q p |
f |
d |
. |
|
dx |
||||
|
|
x 0 |
2.8 Теплопередача через ребристую плоскую стенку
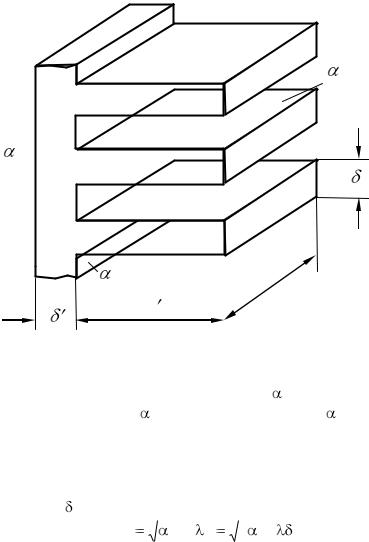
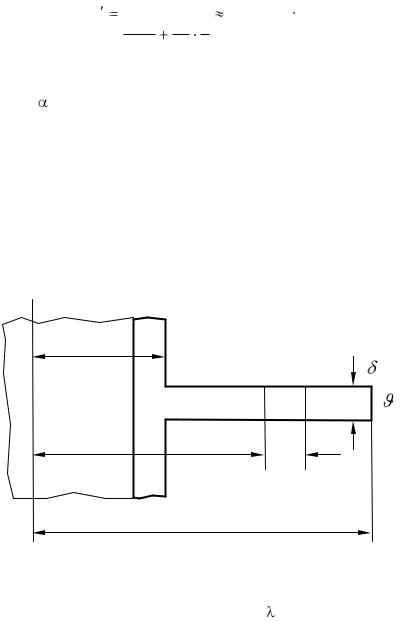
Необходимо найти тепловой поток через плоскую ребристую стенку безграничных размеров. Стенка оребрена со стороны меньшего коэффициента теплоотдачи (рис. 2.14).
198
p
tж1
1
c |
tж2 |
b |
|
||
|
l |
|
|
|
|
Рис. 2.14. Теплопередача через ребристую стенку
Заданы постоянные значения коэффициентов теплоотдачи на не оребренной поверхности стенки 1, гладкой части оребренной поверхности с и на поверхности ребер p. Заданы геометрические размеры ребер (рис. 2.14) и температуры теплоносителей tж1 и tж2.
Поскольку для ребра b >> 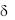 то полагаем, что периметр поперечного сечения ребер u = 2b. Площадь поперечного сечения ребра f = b .
то полагаем, что периметр поперечного сечения ребер u = 2b. Площадь поперечного сечения ребра f = b .
|
|
|
|
|
Следовательно, m |
p u / f |
|
2 p / , 1/м. Подста- |
|
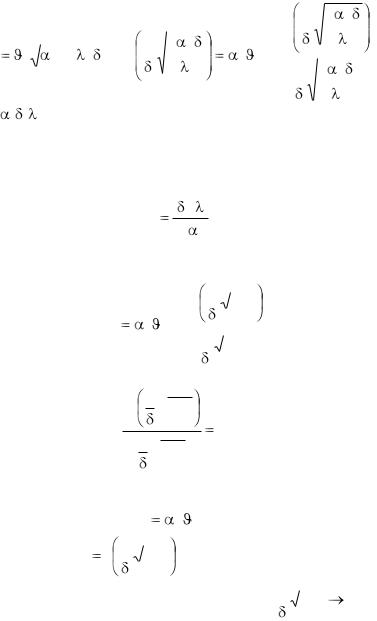
вив полученное выражение для m в уравнение (2.85), умножив и разделив на 2l, получим:
198
|
|
|
|
|
|
|
|
|
|
|
|
|
th |
|
|
l |
2 |
p |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
2l |
|
l |
|
2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
p |
1 |
p |
2b b |
th |
|
F |
|
|
|
|
|
|
|
|
|
|
|
; |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
2l |
|
|
|
|
|
p 1 p |
l |
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
здесь |
p / |
= Bi - безразмерный комплекс, называемый числом |
||||||||||||||||||||||
Био. Число Вi является важной характеристикой процесса теплопроводности. Оно представляет собой отношение внутреннего термического сопротивления теплопроводности к внешнему термическому сопротивлению теплоотдачи:
/
Bi . 1/ p
Окончательно уравнение для теплового потока поверхности ребра можно записать в виде
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
th |
|
|
2Bi |
|
||||||
|
|
|
|
|
||||||||
Qp |
p 1Fp |
|
|
|
|
|
. |
(2.86) |
||||
|
l |
|
|
|
||||||||
|
|
|
|
2Bi |
|
|||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||||
Обозначим:
th l 
 2Bi
2Bi
E .
l 
 2Bi
2Bi
Величина Е называется коэффициентом эффективности ребра. Тогда уравнение (2.86) принимает вид:
|
Qp |
p 1Fp E . |
|
|
|
|
|
|
||
Величина E f |
l |
|
|
стремится |
к |
своему |
макси- |
|||
|
2Bi |
|||||||||
|
|
|||||||||
|
||||||||||
мальному значению, равному единице, при |
|
l |
|
|
|
0 (при |
||||
|
|
2Bi |
||||||||
|
|
|||||||||
заданных геометрических размерах ребра последнее возможно в случае, если
198

0 т. е. Bi |
0). |
|
|
|
|
|
|
|
|
|
|
Теплота Qс, Вт, отдаваемая гладкой частью оребренной |
|||||||||||
поверхности, |
|
|
|
|
|
|
|
|
|
|
|
|
Q c |
|
|
c 1Fc . |
|
|
|
|
|
||
Общее количество теплоты: |
|
|
|
|
|
||||||
|
Q Qp |
Qc |
|
|
p 1Fp E |
|
c 1Fc |
(а) |
|||
или |
|
|
|
|
|
|
|
|
|
|
|
Q |
пр 1Fр.с , |
|
|
|
Fp.c |
Fp |
|
Fc . |
(б) |
||
Из сопоставления (а) и (б) следует, что |
|
||||||||||
|
|
|
|
|
Fp |
|
F |
|
|||
|
|
|
E |
|
|
|
|
|
c |
. |
(2.87) |
|
пр |
p |
|
F |
c |
F |
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
p.c |
|
p.c |
|
|||
Величина пр, входящая в уравнение (2.87), называется приведенным коэффициентом теплоотдачи. Это такой усредненный коэффициент теплоотдачи ребристой стенки, который учитывает теплоотдачу поверхности ребра, поверхности гладкой части стенки и эффективность работы ребра.
Тогда для передачи теплоты через ребристую стенку можно записать систему уравнений:
Q |
1F1 t ж1 t c1 ; Q |
|
t c1 |
|
|
t c2 |
F1 ; Q |
|
|
пр t c2 t ж2 Fp.c . |
|||||
|
|
|
|
|
|||||||||||
|
Здесь . см. рис. 2.14. |
|
|
|
|
|
|
|
|
|
|||||
|
Из этих равнений получаем: |
|
|
|
|
|
|||||||||
|
Q |
|
|
|
|
t |
ж1 |
|
t |
ж 2 |
|
. |
(2.88) |
||
|
|
1 |
|
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1F1 |
|
|
F1 |
|
пр Fp.c |
|
|
|
|||
Если тепловой поток отнести к единице оребренной поверхности стенки, то
Q |
q p.c |
|
|
|
|
t ж1 t ж 2 |
|
|
|
k p.c t ж1 t ж 2 , (2.88) |
|||
F |
1 |
|
Fp.c |
|
|
|
Fp.c |
1 |
|
||||
p.c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
F1 |
|
|
|
F1 |
|
пр |
|
|
||
где
198

k p.c |
|
|
|
t ж1 |
|
t ж 2 |
|
|
|
||
|
1 |
|
Fp.c |
|
|
|
Fp.c |
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
F1 |
|
F1 |
|
пр |
|
||
— коэффициент теплопередачи через ребристую стенку при отнесении теплового потока к оребренной поверхности, Вт/(м2 К).
Если тепловой поток отнести к неоребренной поверхности стенки, то получим:
|
Q |
q1 |
|
|
|
t ж1 |
t ж 2 |
|
|
|
|
|
|
k1 t ж1 t ж 2 , |
(2.90) |
|||||||||
|
F |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
пр |
|
Fp.c |
|
||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
t ж1 |
|
|
t ж 2 |
|
|
||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 F1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1пр Fp.c
—коэффициент теплопередачи при отнесении теплового потока к неоребренной поверхности стенки.
Отношение оребренной поверхности Fр.с к гладкой F1 называется коэффициентом оребрения.
Влияние оребрения на коэффициент теплопередачи мож-
но показать на следующем примере. Пусть 1 = 1000 и 1 = 20
Вт/(м2 К). Предположим, что |
/ |
мало и им можно пренеб- |
||||||||||
речь, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
1 |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
1 |
|
||||||
|
|
|
|
|
|
F1 |
|
|||||
|
|
1 |
|
|
пр |
|
|
Fp.c |
||||
Для плоской поверхности (коэффициент оребрения Fр.с/F1 |
||||||||||||
равен единице) получим: |
|
|
|
|
|
|
|
|
|
|
|
|
k1 |
|
1 |
|
|
|
|
20 Вт/(м2 К). |
|||||
|
|
|
|
|
|
|||||||
1 |
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|||||
1000 20
Если стенка имеет ребра с одной стороны, причем коэф-
198
фициент Fр.с/F1 = 2, то:
k1 |
|
1 |
|
40 |
Вт/(м2 К). |
|
|
|
|
||||
1 |
1 |
1 |
||||
|
|
|
1000 20 2
Следовательно при заданных соотношениях коэффициентов теплоотдачи при оребрении плоской стенки со стороны малого с коэффициентом оребрения Fр.с/F1 = 2, передача теплоты увеличивается примерно в 2 раза.
2.9 Теплопроводность круглого ребра постоянной толщины
Ребра, имеющие переменное поперечное сечение по высоте, рассчитываются значительно сложнее, чем прямые ребра постоянного сечения. Рассмотрим расчет теплопроводности круглого ребра постоянной толщины (рис. 2.15). Круглые ребра применяются при оребрении цилиндрических поверхностей (труб).
r1
2
r dr
r2
Рис. 2.15 Перенос теплоты через круглое ребро постоянной толщины
Заданы внутренний радиус ребра r1, наружный r2, толщина  и коэффициент теплопроводности . Температура среды tж = const. Избыточная температура ребра будет:
и коэффициент теплопроводности . Температура среды tж = const. Избыточная температура ребра будет:
198

t t ж .
Задан постоянный коэффициент теплоотдачи |
на всей |
поверхности ребра и температура у основания ребра |
1. |
Режим стационарный, и температура изменяется только по высоте ребра. Найдем для этих условий дифференциальное уравнение, которым описывается процесс теплопроводности в ребре. Составам уравнение баланса энергии для кольцевого элемента ребра толщиной dr:
Q r |
Q r dr |
dQ . |
|
(2.91) |
|||||
Находя составляющие уравнения (2.91), получаем диф- |
|||||||||
ференциальное уравнение вида: |
|
|
|
|
|||||
|
d 2 |
1 d |
2 |
0 . |
(2.92) |
||||
|
|
|
|
|
|
|
|
||
|
dr 2 |
|
r dr |
|
|
||||
|
|
|
|
|
|
||||
Обозначим 2 /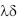 = m2, mr = z и 1/r = m/z; тогда уравнение (2.82) после подстановки d /dr = md /dz и d2 /dr2 = m2(d2 /dz2) принимает вид:
= m2, mr = z и 1/r = m/z; тогда уравнение (2.82) после подстановки d /dr = md /dz и d2 /dr2 = m2(d2 /dz2) принимает вид:
|
d2 |
|
1 d |
0 . |
(2.93) |
||
|
|
|
|
|
|
||
|
dz 2 |
|
z dz |
||||
|
|
|
|
||||
Уравнение (2.93) представляет собой уравнение Бесселя, |
|||||||
имеющее общее решение вида |
|
|
|||||
|
|
C1I0 z C2 K 0 z , |
(2.94) |
||||
где I0(z) = I0(mr) . модифицированная функция Бесселя первого рода нулевого порядка; K2(z) = K0(mr) . модифицированная функция Бесселя второго рода нулевого порядка.
Эти функции имеют следующие свойства:
при r = 0 |
I0(mr) = 1 и K0(mr) |
; |
|
при r = |
I0(mr) |
и K0(mr) = 0 |
|
Постоянные С1 |
и С2 определяются из граничных усло- |
||
вий. |
|
|
|
198
2.10 Теплопроводность прямого ребра переменного сечения
При конструировании систем охлаждения для целого ряда машин, в особенности для летательных аппаратов, приобретает особую важность решение задачи максимального теплообмена при минимальной массе теплообменника. Возникает вопрос о том, какова оптимальная форма сечения ребра, имеющего минимальную массу при заданном тепловом потоке.
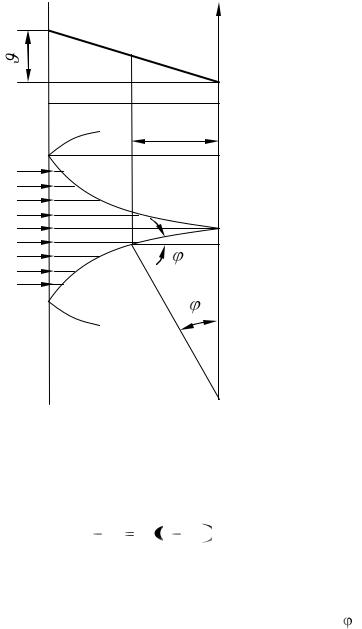
Ребро с минимальной массой. Существо вопроса сводится к тому, чтобы каждая часть ребра использовалась с одинаковым эффектом, т. е. плотность теплового потока должна оставаться постоянной по всему поперечному сечению ребра. Это значит, что линии теплового потока должны быть параллельными оси ребра. При этих условиях температура вдоль линии теплового потока будет изменяться по линейному закону (рис. 2.17).
198
1
t1 |
t |
t
tж
0
h x
Рис. 2.17. Сечение ребра минимального веса.
При заданной температуре у основания ребра t1 и температуре вершины ребра, близкой к температуре окружающей среды tж в силу одномерности задачи для любого сечения ребра можно записать:
t t ж |
x |
t1 t ж , |
(2.99) |
|
h |
||||
|
|
|
где x – расстояние по оси ребра от его вершины; h – полная высота ребра.
Рассмотрим элемент поверхности ребра на расстоянии x. Пусть этот участок поверхности образует с осью ребра угол . Если плотность теплового потока вдоль оси ребра равна q, то
198
