
Методическое пособие 699
.pdf
и с достаточной точностью можно ограничиться первым членом ряда:
ln |
d 2 |
|
d 2 |
1 |
d 2 |
d1 |
2 |
, |
|||
d1 |
|
d1 |
d1 |
|
|
|
d1 |
||||
где - толщина цилиндрической стенки, м. |
|
|
|||||||||
Подставив полученное значение |
ln |
d 2 |
в уравнение (2- |
||||||||
d1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||
52), получим:
k |
|
1 |
|
|
|
. |
(2.53) |
||
|
|
|
|
|
|
||||
|
1 |
|
|
|
1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
Следовательно, если стенка трубы тонкая, то при практи- |
|||||||||
ческих расчетах можно пользоваться формулой |
|
||||||||
Q |
k dx l(t ж1 |
t ж2 ) , |
(2.54) |
||||||
где k, Вт/(м2 К) взят согласно формуле (2-53), т.е. как для плоской стенки. При этом если d2/d1 < 2, погрешность расчета не превышает 4%. Для многих технических расчетов ошибка, не превышающая 4% вполне допустима. Обычно в инженерных расчетах при d2/d1 1,8 пользуются формулой (2-54).
2.3 Критический диаметр цилиндрической стенки
Рассмотрим влияние изменение диаметра на термическое сопротивление однородной цилиндрической стенки. Из (2.51) имеем:
R l |
1 |
|
1 |
|
1 |
ln |
d 2 |
|
1 |
|
. |
k l |
|
1d1 |
2 |
d1 |
|
2 d |
2 |
||||
|
|
|
|
|
|||||||
При постоянных значениях |
1, d1, |
и 2 |
полное термиче- |
||||||||
ское сопротивление теплопередачи цилиндрической стенки будет зависеть от внешнего диаметра. Из уравнения (2.51) следует, что при этих условиях 1/ 1d1 Rl1 = const. .
Термическое сопротивление теплопроводности
198

1 |
ln |
d 2 |
R lc |
с увеличением d2 будет возрастать, а термиче- |
||
2 |
d |
1 |
||||
|
|
|
||||
ское сопротивление теплоотдачи 1/ 2d2  Rl2 будет уменьшаться. Очевидно, что полное термическое сопротивление будет определяться характером изменения составляющих Rlc и Rl2. Изменение частных термических сопротивлений изображено на рис. 2.8.
Rl2 будет уменьшаться. Очевидно, что полное термическое сопротивление будет определяться характером изменения составляющих Rlc и Rl2. Изменение частных термических сопротивлений изображено на рис. 2.8.
Для того чтобы выяснить, как будет изменяться Rl при изменении толщины цилиндрической стенки, исследуем Rl как функцию d2. Возьмем производную от Rl, по d2 и приравняем нулю:
d(R l ) |
|
1 |
|
|
1 |
0 . |
||
d d |
2 |
|
2 d |
2 |
2 |
d 2 |
||
|
|
|||||||
|
|
|
2 |
|
||||
Значение d2 из последнего выражения со ответствует экстремальной точке кривой Rl = f (d2). Исследовав кривую любым из известных способов на максимум и минимум увидим, что в экстремальной точке имеет место минимум. Таким образом, при значении диаметра d2 = 2 / 2 термическое сопротивление теплопередачи будет минимальным.
198
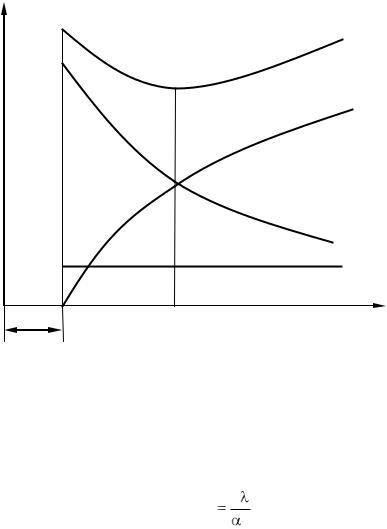
Rl |
Rl об |
Rl с
Rl2
Rl1 d2
dкр
d2 = d1
Рис. 2.8 Зависимость термического сопротивления цилиндрической сетки от d2
Значение внешнего диаметра трубы, соответствующего минимальному полному термическому сопротивлению теплопередачи, называется критическим диаметром и обозначается dкр. Рассчитывается он по формуле
d кр |
2 |
. |
(2.60) |
|
2
При d2 < dкр c увеличением d2 полное термическое сопротивление теплопередачи снижается, так как увеличение наружной поверхности оказывает на термическое сопротивление большее влияние, чем увеличение толщины стенки.
При d2 > dкр с увеличением d2 термическое сопротивле-
198
ние теплопередачи возрастает, что указывает на доминирующее влияние толщины стенки.
Изложенные соображения необходимо учитывать при выборе тепловой изоляции для покрытия различных цилиндрических аппаратов и трубопроводов.
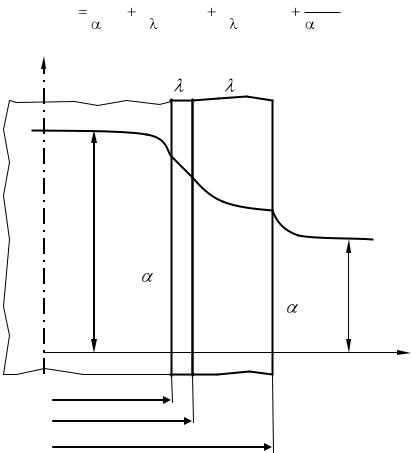
Рассмотрим критический диаметр изоляции, наложенной на трубу (рис. 2.9). Термическое сопротивление теплопередачи для такой трубы запишется:
1 |
1 |
|
|
d |
2 |
1 |
|
d |
3 |
|||
R l |
|
|
|
ln |
|
|
|
|
|
ln |
|
|
1d1 |
|
2 c |
|
d1 |
|
2 из |
d 2 |
|||||
|
|
|
|
|
|
|||||||
t |
|
|
|
1 |
|
|
из |
|
|
|
||
tж1
1
2
0
d1 d2
d3
1
2 d 3 .
tж2
Рис. 2.9 К понятию критического диаметра изоляции
198

Из уравнения ql 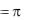 t / R l следует, что ql при увеличении
t / R l следует, что ql при увеличении
внешнего диаметра изоляции d3 сначала будет возрастать и при d3 = dкр будет иметь максимум ql. При дальнейшем увеличении внешнего диаметра изоляции ql будет снижаться (рис. 2- 10).
ql
|
|
d3 |
d2 |
dкр |
d3 эф |
Рис. 2.10 Зависимость тепловых потерь от толщины изоляции, наложенной на цилиндрическую стенку
Выбрав какой-либо теплоизоляционный материал для покрытия цилиндрической поверхности, прежде всего нужно рассчитать критический диаметр по формуле для заданных из
и2.
Если окажется, что величина dкр больше наружного диаметра трубы d2 то применение выбранного материала в качестве тепловой изоляции нецелесообразно. В области d2 < d3 < dкр.из при увеличении толщины изоляции будет наблюдаться увеличение теплопотерь. Это положение наглядно иллюстри-
198

руется на рис. 2.10. Только при d3 = d3эф тепловые потери вновь станут такими же, как для первоначального, неизолированного трубопровода. Следовательно, лишний слой тепловой изоляции не будет оправдывать своего назначения.
Значит, для эффективной работы тепловой изоляции необходимо, чтобы dкр.из d2.
Пример. Трубу внешним диаметром d = 20 мм необходимо покрыть тепловой изоляцией. В качестве изоляции может
быть взят асбест с коэффициентом теплопроводности |
= 0,1 |
Вт/(м К), коэффициент теплоотдачи во внешнюю среду |
2 = 5 |
Вт/(м2 К). Целесообразно ли в данном случае использовать асбест в качестве материала для тепловой изоляции?
Критический диаметр изоляции
d |
|
2 из |
кр.из |
||
|
2 |
|
2 |
0,1 |
0,04 |
м = 40 мм. |
|
|
||
|
5 |
||
|
|
|
Так как d2 < dкр.из асбест в рассматриваемом случае использовать нецелесообразно.
2.4 Передача теплоты через шаровую стенку
а) Граничные условия первого рода
Пусть имеется полый шар с радиусами r1 и r2, постоянным коэффициентом теплопроводности и с заданными равномерно распределенными температурами поверхностей tc1 и
tc2.
Так как в рассматриваемом случае температура измеряется только в направлении радиуса шара, то дифференциальное уравнение тепловодности в сферических координатах принимает вид:
2 t |
d 2 t |
|
2 dt |
0 . |
(2.61) |
|||
|
|
|
|
|
|
|||
dr |
2 |
|
r dr |
|||||
|
|
|
|
|||||
Граничные условия запишутся:
198

при r |
r1 |
t |
|
|
t c1 ; |
|
|
|
(2.62) |
|||||||||||
при r |
r2 |
t |
|
|
t c2 . |
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
После первого интегрирования уравнения (2.61) получа- |
||||||||||||||||||||
ем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
C1 |
|
. |
|
|
|
|
|
|
|
|
|
(а) |
|||
|
|
dr |
|
r 2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Второе интегрирование дает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
t |
C |
|
|
|
|
|
C1 |
. |
|
|
|
(2.63) |
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
r |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Постоянные интегрирования в уравнении (2.63) опреде- |
||||||||||||||||||||
ляются из граничных условий (2.62). При этом получим: |
|
|||||||||||||||||||
C |
|
|
t c1 |
|
|
|
t c2 |
; |
|
|
|
(б) |
||||||||
1 |
|
|
1 |
|
|
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
r1 |
|
|
|
|
r2 |
|
|
|
|
|||||||
C2 |
|
t c1 |
|
t c1 |
|
|
|
t c2 |
1 |
. |
(в) |
|||||||||
|
|
|
1 |
1 |
|
|
|
r |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
r2 |
|
|
|
|
||||
Подставляя значения С1 и С2 в уравнение (2.63), получаем выражение для температурного поля в шаровой стенке:
t t c1 |
t c1 |
t c2 |
|
1 |
1 |
. |
(2.64) |
||
1 |
1 |
|
r1 |
|
r |
|
|||
|
|
|
|
|
|||||
r1 r2
Для нахождения количества теплоты, проходящей через шаровую поверхность величиной F в единицу времени, можно воспользоваться законом Фурье:
Q 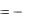 drdt F
drdt F 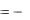 4 r 2 drdt ;
4 r 2 drdt ;
здесь Q измеряется в ваттах.
Если в это выражение подставить значение градиента температуры dt/dr, то получим:
198

Q |
4 t c1 |
t c2 |
|
2 |
|
t |
|
|
d1d 2 |
t . |
(2.65) |
||||
1 |
|
1 |
|
1 |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
d1 |
|
d 2 |
|
|
|
|
|
|
|
r |
r |
|
|
|
|
|
|
|
|
||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
Эти уравнения являются расчетными формулами теплопроводности шаровой стенки. Из уравнения (2.64) следует, что при постоянном температура в шаровой стенке меняется по закону гиперболы.
б) Граничные условия третьего рода (теплопередача)
При заданным граничных условиях третьего рода кроме r1 и r2 будут известны tж1 и tж2, а также коэффициенты теплоотдачи на поверхности шаровой стенки 1 и 2. Величины tж1, tж2, 1 и 2 предполагаются постоянными во времени, а 1 и 2
– и по поверхностям.
Поскольку процесс стационарный и полный тепловой поток Q, Вт, будет постоянным для всех изотермических поверхностей, то можно записать:
Q |
|
|
d 2 |
t |
|
|
|
|
t |
|
|
; |
|
|
|
|
|
|
|
|
Q |
|
|
|
2 |
|
|
|
|
|
t |
|
|
t |
|
; |
|||||
1 |
|
ж1 |
c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 |
c2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1 |
|
|
|
|
d 2 |
|
|
|
|
|
|
||
|
|
|
|
|
Q |
|
2 |
|
d |
2 |
t |
c2 |
|
|
t |
ж2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из этих уравнений следует, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Q |
|
|
|
|
|
|
|
|
|
|
t |
ж1 |
|
|
|
t ж 2 |
|
|
|
|
|
|
|
|
|
|
|
k ш t . |
|
|
(2.66) |
|||||||||
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
d 2 |
2 |
|
|
|
d |
1 |
|
|
|
d |
2 |
|
|
|
|
2 |
d 2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
k ш |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1d12 |
|
|
|
2 d1 |
|
|
|
d 2 |
|
|
|
|
|
2 d 22 |
|
|
|
|
|
||||||||||||
называется коэффициентом теплопередачи шаровой стенки и измеряется в Вт/К.
198

Обратная величина
1 |
R |
1 |
1 |
1 |
1 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
ш |
d 2 |
2 |
|
d |
|
|
d |
|
|
|
d 2 |
|||
ш |
|
1 |
|
1 |
|
2 |
2 |
|||||||||
|
|
1 |
|
|
|
|
|
|
2 |
|||||||
называется термическим сопротивлением теплопередачи шаровой стенки и измеряется в К/Вт.
2.5 Обобщенный метод решения задач теплопроводности в плоской, цилиндрической и шаровой стенках
Для процесса теплопроводности в плоской, цилиндрической и шаровой стенках можно предложить обобщенное решение как при постоянном коэффициенте теплопроводности так и в случае зависимости последнего от температуры.
Рассмотрим одномерную задачу для всех трех случаев при постоянном коэффициенте теплопроводности стенки. При этом зависимость температуры в пространстве для плоской стенки представим как t = f1(x), для цилиндрической стенки t = f2(r) и для шаровой стенки t = f3(r)
Если принять, что изотермические поверхности в рассматриваемых телах замкнуты, то температура становится функцией только координаты n, являющейся нормалью к изотермическим поверхностям, тепловой поток будет пропорционален градиенту температуры t/ n, а величина поверхности выразится функцией F = F(n).
Замкнутость изотермических поверхностей для цилиндра и шара очевидна, а пластину будем рассматривать как предельный случай замкнутой системы, когда n 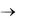 .
.
Вследствие замкнутости изотермических поверхностей тепловой поток через стенку любого из рассматриваемых тел можно представить как
Q |
dt |
F(n) . |
(2.67) |
|
dn |
||||
|
|
|
Так как Q = const для любой изотермической поверхности, то, разделяя переменные в уравнении (2-67) и интегрируя в пределах от n = n1 до n = n2 и соответственно от tc1 до tc2 по-
198
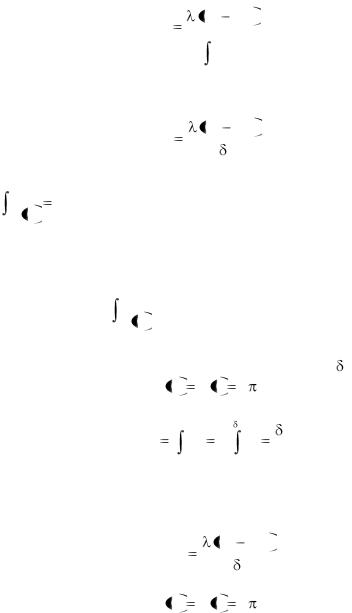
лучим: |
|
|
|
|
|
|
|
|
Q |
t c1 |
t c2 |
. |
(2.68) |
||||
n 2 |
|
|||||||
|
dn |
|
||||||
|
|
|
|
|
|
|
|
|
|
n |
1 |
F(n) |
|
||||
Видим, что формула (2-68) аналогична ранее полученной |
||||||||
для плоской стенки: |
|
|
|
|
|
|
|
|
q |
t c1 |
t c2 |
. |
|
||||
|
|
|
|
|
||||
При этом Q аналогично плотности тѐплового потока q, а
n 2
n1
dn |
In 2 |
- толщине стенки, которую в дальнейшем усло- |
|
||
|
||
F n |
n |
|
1 |
|
|
|
|
вимся называть приведенной толщиной стенки. Формула (2.68) является общей для описания теплового потока через стенки всех трех геометрических форм.
n 2
Величина
n1
dn |
зависит только от геометрической фор- |
|
|
||
F n |
||
|
мы стенки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
а) Для плоской пластины n = x, n1 = 0 и n2 = |
, а |
||||||||||||
|
F n |
|
F r |
|
|
2 |
rl , |
|
|
|
|
||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 2 |
dn |
1 |
|
|
|
|
|
|
|
|||
In 2 |
|
|
|
|
|
|
dx |
|
. |
|
|
||
|
|
|
|
|
|
|
|
|
|||||
n |
n |
|
F |
F 0 |
|
|
F |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Подставляя полученное значение |
I n 2 |
в уравнение (2.68), |
|||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
приходим к выражению теплового потока Q, Вт, для плоской |
|||||||||||||
пластины: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
t c1 |
|
t c2 |
F . |
|
(2.69) |
||||
|
|
|
|
|
|
|
|
|
|||||
б) Для цилиндрической стенки n = r, n1 = r1 |
и n2_ = r2, а |
||||||||||||
|
F n |
|
F r |
|
|
2 |
rl , |
|
|
|
|
||
тогда
198
