
Методическое пособие 699
.pdf
Постоянная 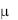 в уравнении (3.46) определяется из граничных условий (r = r0), решение которых приводит к характеристическому уравнению
в уравнении (3.46) определяется из граничных условий (r = r0), решение которых приводит к характеристическому уравнению
J 0 |
Bi ; |
(3.47) |
J1 |
здесь J1 ( ) — функция Бесселя первого рода первого порядка. Уравнение (3.47) является трансцендентным, и его удоб-
но решать графическим способом, обозначив:
/ Bi y1 ; J 0 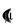 / J1
/ J1 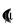
 y2 .
y2 .
Отметим, что y2 обращается в нуль в тех точках, для ко-
торых J0( ) = 0.
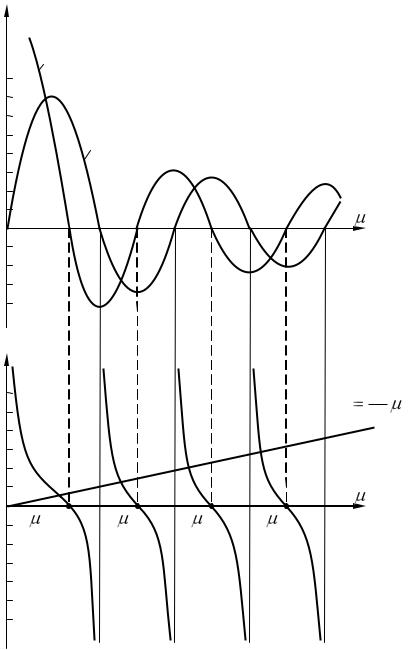
В тех точках, в которых функция J1( 1) обращается в нуль, функция y2 претерпевает разрыв непрерывности и становится равной ± . Функции J0( ) и J1( ) являются периодическими затухающими функциями, а кривая y2 = J0( )/J1( ) напоминает котангенсоиду, но с убывающим периодом. Функция y1 = /Bi графически представляет прямую линию, проходящую через начало координат. Выполнив построение, как показано на рис. 3.10, в точках пересечения функции у2 с прямой y1 получим значения корней характеристического уравнения (3.47). Из рис. 3.10 следует, что уравнение (3.47) имеет бесчисленное множество решений, а сами корни, как и для пла-
стины, представляют ряд возрастающих чисел, т. е. |
1 < |
2 < |
3 |
< ... < n где n = 1, 2, 3, ..., . |
|
|
|
Первые четыре корня уравнения (3.47) 1, |
2, |
3 и |
4 |
приведены в табл. 3.2 для различных значений числа Bi (от 0 до ).
Общее решение будет суммой всех частных решений
(3.46):
n |
|
|
r |
|
|
|
|
|
|
Cn J |
|
exp |
2 |
|
. |
(3.48) |
|
n 1 |
0 n r |
n |
r 2 |
|||||
|
|
0 |
|
|
0 |
|
|
|
Постоянная Сn в уравнении (3.48) находится из начальных условий.
198
При = 0 |
= 0 |
= F(r) и уравнение (3.48) принимает |
||||
вид: |
|
|
|
|
|
|
|
|
n |
r |
|
|
|
|
F r |
Cn J0 |
. |
(3.49) |
||
0 |
|
|||||
r0 |
||||||
|
|
n 1 |
|
|
||
198
J
J0
0,8
0,6
0,4
0,2
0
-0,2 -0,4
y 6
4
2
0
-2 -4 -6
J1
1 |
2 |
3 |
4 5 6 |
7 |
8 |
10 |
11 12 13 |
y
1 y1 Bi
3 |
4 |
6 |
7 |
9 |
10 11 |
1213 14 |
1 |
|
2 |
3 |
|
|
4 |
Рис. 3.10 К решению уравнения (3-47)
198

Видим, что (3.49) представляет собой разложение функции F(r) в ряд Фурье по функциям Бесселя, а для такой последовательности числа Cn определяются по формуле
|
|
|
|
|
|
|
r0 |
|
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rF r J 0 |
n |
|
dr |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
0 |
r |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
. |
|
|
|
|
|
(3.50) |
||||||
|
|
|
|
|
Cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
r0 |
|
|
|
|
r |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
rJ2 0 |
|
|
|
|
dr |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
n |
|
|
r |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.2 |
|
|
|
|
|
|
|
Значения |
n для цилиндра |
|
|
|
|
|
|||||||||||||
Bi |
1 |
|
|
2 |
|
3 |
|
|
4 |
|
|
|
|
Bi |
|
1 |
|
|
|
2 |
3 |
4 |
|||
0,0 |
0,0000 |
|
3,8317 |
7,0156 |
|
10,1735 |
|
2,0 |
|
1,5954 |
|
4,2910 |
7,2884 |
10,3658 |
|||||||||||
0,01 |
0,1412 |
|
3,8343 |
7,0170 |
|
10,1745 |
|
3,0 |
|
1,7887 |
|
4,4634 |
7,4108 |
10,4566 |
|||||||||||
0,02 |
0,1995 |
|
3,8369 |
7,0184 |
|
10,1754 |
|
4,0 |
|
1,9081 |
|
4,6018 |
7,5201 |
10,5423 |
|||||||||||
0,04 |
0,2814 |
|
3,8421 |
7,0213 |
|
10,1774 |
|
5,0 |
|
1,9898 |
|
4,7131 |
7,6177 |
10,6223 |
|||||||||||
0,06 |
0,3438 |
|
3,8473 |
7,0241 |
|
10,1794 |
|
6,0 |
|
2,0490 |
|
4,8033 |
7,7039 |
10,6964 |
|||||||||||
0,08 |
0,3960 |
|
3,8525 |
7,0270 |
|
10,1813 |
|
7,0 |
|
2,0937 |
|
4,8772 |
7,7797 |
10,7646 |
|||||||||||
0,10 |
0,4417 |
|
3,8877 |
7,0298 |
|
10,1833 |
|
8,0 |
|
2,1286 |
|
4,9384 |
7,8464 |
10,8271 |
|||||||||||
0,15 |
0,5376 |
|
3,8706 |
7,0369 |
|
10,1882 |
|
9,0 |
|
2,1466 |
|
4,9897 |
7,9051 |
10,8842 |
|||||||||||
0,20 |
0,6170 |
|
3,8835 |
7,0440 |
|
10,1931 |
|
10,0 |
|
2,1795 |
|
5,0332 |
7,9569 |
10,9363 |
|||||||||||
0,30 |
0,7465 |
|
3,9091 |
7,0582 |
|
10,2029 |
|
15,0 |
|
2,2509 |
|
5,1773 |
8,1422 |
11,1367 |
|||||||||||
0,40 |
0,8516 |
|
3,9344 |
7,0723 |
|
10,2127 |
|
20,0 |
|
2,2880 |
|
5,2568 |
8,2534 |
11,2677 |
|||||||||||
0,50 |
0,9408 |
|
3,9594 |
7,0864 |
|
10,2225 |
|
30,0 |
|
2,3261 |
|
5,3410 |
8,3771 |
11,4221 |
|||||||||||
0,60 |
1,0184 |
|
3,9841 |
7,1004 |
|
10,2322 |
|
40,0 |
|
2,3455 |
|
5,3846 |
8,4432 |
11,5081 |
|||||||||||
0,70 |
1,0876 |
|
4,0085 |
7,1143 |
|
10,2419 |
|
50,0 |
|
2,3572 |
|
5,4112 |
8,4840 |
11,5621 |
|||||||||||
0,80 |
1,1490 |
|
4,0325 |
7,1282 |
|
10,2519 |
|
60,0 |
|
2,3651 |
|
5,4291 |
8,5116 |
11,5990 |
|||||||||||
0,90 |
1,2048 |
|
4,0562 |
7,1421 |
|
10,2213 |
|
80,0 |
|
2,3750 |
|
5,4516 |
8,5466 |
11,6461 |
|||||||||||
1,0 |
1,4558 |
|
4,0795 |
7,1558 |
|
10,2710 |
|
100,0 |
|
2,3809 |
|
5,4652 |
8,5678 |
11,6747 |
|||||||||||
1,5 |
1,4569 |
|
4,1902 |
7,2233 |
|
10,3188 |
|
|
|
|
|
|
|
2,4048 |
|
5,5201 |
8,6537 |
11,9309 |
|||||||
|
После интегрирования знаменателя получаем: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
r0 |
|
|
|
|
|
r |
|
|
|
|||
|
|
Cn |
|
|
|
|
|
|
|
|
|
rF r J0 |
|
|
dr . |
(3.51) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||||
|
|
|
r 2 |
J 2 |
|
J 2 |
|
|
|
|
|
|
r |
||||||||||||
|
|
|
|
0 |
0 n |
1 |
n |
0 |
|
|
|
|
|
|
0 |
|
|
|
|||||||
|
Подставляя полученное выражение для Сn |
в уравнение |
|||||||||||||||||||||||
(3.48), получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
198
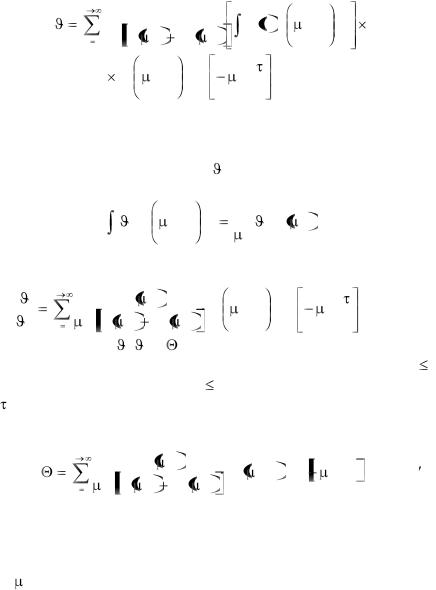
n |
|
|
|
r |
r0 |
|
r |
|
|
|
|
|
rF r J 0 |
|
dr |
||
|
|
|
|
|
|
|
||
n 1 |
r 2 |
J 2 |
n |
J 2 |
n r |
|||
|
0 |
0 |
1 n |
0 |
0 |
|
||
J |
|
r |
exp |
2 |
a |
|
. |
(3.52) |
0 n r |
n |
r |
2 |
|||||
|
0 |
|
|
0 |
|
|
||
Уравнение (3.52) справедливо при любом начальном распределении температуры з цилиндре.
Если в начальный момент времени ( = 0) температура распределена равномерно, т. е. 0 = F(r) = const, то интеграл в уравнении (3.52)
= 0) температура распределена равномерно, т. е. 0 = F(r) = const, то интеграл в уравнении (3.52)
r0 |
|
r |
|
r 2 |
|
r 0 J0 |
|
|
dr |
0 |
0 J1 n . |
n |
r |
|
|||
0 |
|
|
n |
||
|
0 |
|
|||
Для этих условий уравнение температурного поля принимает вид:
|
|
n |
|
|
2J1 |
|
|
|
|
r |
|
|
a |
|
|
|
|
|
|
n |
|
J0 |
|
exp |
2 |
. (3.53) |
|||
|
|
n 1 |
|
J 2 |
|
J 2 |
|
n r |
n |
r 2 |
||||
0 |
|
|
n |
0 |
n |
1 |
n |
0 |
|
|
0 |
|
||
|
Обозначим: |
/ |
0 = |
. безразмерная температура; r/r0 = R |
||||||||||
—безразмерная координата, которая изменяется в пределах 0 |
|
R |
1; |
a/г20 = Fo — число Фурье для цилиндра.
Сучетом этих обозначении последнее выражение запишется в виде
n |
2J1 |
|
|
|
|
|
|
|
|
|
|
n |
|
J |
|
|
R exp |
2 Fo . (3.53 ) |
|
|
|
|
|
|
0 |
n |
|||
n 1 n J 02 |
|
J12 |
|
|
|
n |
|||
n |
n |
|
|
|
|
||||
Заметим, что все принципиальные выводы, сделанные при анализе решения для пластины, справедливы и для цилиндра.
Из характеристического уравнения (3.47) видно, что корни n зависят только от Bi. Поэтому уравнение температурного поля можно представить в виде обобщенной функции от безразмерных параметров:
198

F |
r |
, |
r0 |
, |
a |
|
F R, Bi, Fo . |
(3.54) |
r |
|
r |
2 |
|||||
|
|
|
|
|
|
|||
|
0 |
|
0 |
|
|
|||
Если рассматривать значение температуры на оси цилиндра (R = 0), то уравнение (3.53) запишется следующим образом:
|
|
2J1 |
n |
|
exp |
2 Fo . |
(3.55) |
|
|
|
|
|
|||
n 1 n J 02 |
|
J12 |
|
|
n |
|
|
n |
n |
|
|
||||
На поверхности цилиндра
|
|
|
2J1 n |
|
|
J |
|
exp |
2 Fo |
. (3.56) |
R 1 |
|
|
|
|
0 n |
|||||
J 02 |
|
J12 |
|
|
|
n |
|
|||
n 1 n |
n |
n |
|
|
|
|
||||
При Bi  (практически Bi > 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий J0( ) = 0.
(практически Bi > 100) прямая совпадает с осью абсцисс и корни характеристического уравнения не зависят от Bi, а определяются из условий J0( ) = 0.
В этом случае процесс охлаждения определяется физическими свойствами тела и его геометрическими размерами. При этом уравнение (3.53) принимает вид:
|
2 |
J 0 n R exp |
n2 Fo . |
(3.57) |
|
|
|
|
|||
|
n 1 n J1 n |
||||
|
|
|
|
||
|
Если рассматривать охлаждение цилиндра при условии |
||||
Bi |
0 (практически Bi < 0,l), то при разложении функций |
||||
J0( |
) и J1( ) в степенные ряды они становятся настолько быст- |
||||
росходящимися, что можно ограничиться первыми членами ряда, и тогда 2 = 2Bi.
Действительно,
|
1 |
1 |
|
2 |
|
... |
|
|||||
J 0 |
22 |
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
J1 |
|
Bi 1 |
1 |
|
3 |
... |
||||||
|
|
|
||||||||||
|
|
2 |
|
22 |
|
4 |
|
|
||||
|
|
|
|
|
|
|||||||
откуда получаем:
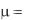

 2Bi .
2Bi .
Кроме того, коэффициенты всех членов ряда бесконечной суммы (3.53) равны нулю, за исключением коэффициента
198
D1 |
|
|
2J1 |
1 |
|
, |
|
|
J 2 |
|
J 2 |
|
|
||
1 |
1 |
1 |
|
|
|||
0 |
1 |
|
|
||||
который равен единице. Уравнение (3.53) для условий Bi |
0 |
||||||
принимает вид: |
|
|
|
|
|
|
|
J |
0 |
|
1 |
R exp |
2 Fo . |
(3.58) |
||
|
|
|
|
|
1 |
|
||
На оси цилиндра (R = 0): |
|
|
|
|
|
|||
R |
|
0 |
|
exp |
2 Fo . |
(3.59) |
||
|
|
|
|
|
1 |
|
||
На поверхности цилиндра (R = 1): |
|
|||||||
R 1 |
|
J |
0 |
1 |
exp |
2 Fo . |
(3.60) |
|
|
|
|
1 |
|
||||
|
|
|
|
|
||||
В силу того что |
|
2Bi , как сама функция J0( |
1), так и |
|||||
отношение температур на оси и поверхности цилиндра будут стремиться к единице, т. е.
R 0 |
|
exp |
12 Fo |
1. |
R 1 |
|
J 0 1 exp |
12 Fo |
|
|
|
Последнее указывает на то, что температура по толщине цилиндра распределена равномерно и практически не зависит от радиуса цилиндра. Задача становится внешней и протекание процесса определяется условиями охлаждения на поверхности цилиндра.
Если Fo 0,25, при вычислении безразмерной температуры можно ограничиться первым членом ряда. Допускаемая при этом ошибка не превысит 1%. Тогда безразмерные температуры на оси и поверхности цилиндра могут быть вычислены по формулам:
на оси цилиндра
R 0 |
N |
0 |
Bi exp |
2 Fo ; |
(3.61) |
|
|
1 |
|
||
на поверхности цилиндра |
|
|
|
||
|
P |
Bi exp |
2 Fo . |
(3.62) |
|
|
0 |
|
|
1 |
|
Функции N0(Вi) и P0(Bi) могут быть заранее рассчитаны и сведены в таблицы (см. [Л. 82, 164, 182]). Поскольку в уравнениях (3.61) и (3.62) является функцией только двух безразмерных параметров
198

R 0 |
Ф1 |
Bi, Fo |
и |
|
|
R 1 |
Ф2 |
Bi, Fo , |
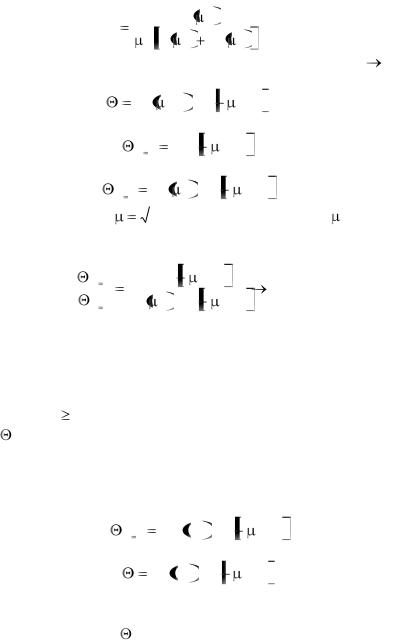
то для определения температуры на оси поверхности цилиндра можно построить графики, показанные на рис. 3.11 и 3.12.
198
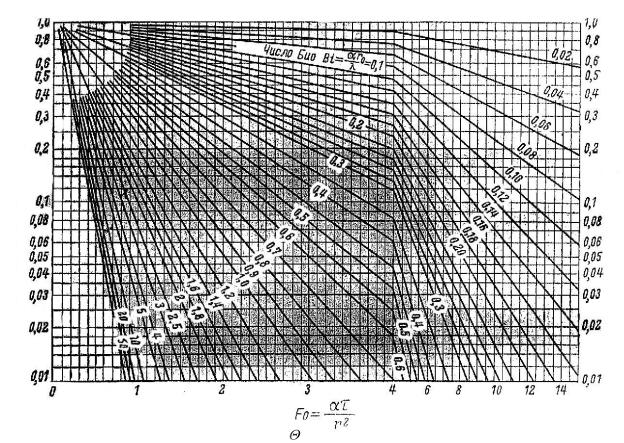
Рис. 3.11 Зависимость = Ф1 (Fo, Bi) для оси цилиндра
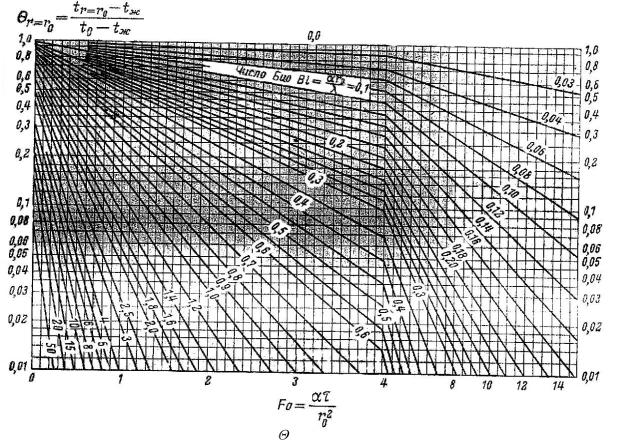
Рис. 3.12 Зависимость = Ф2 (Fo, Bi) для оси цилиндра
