
Методическое пособие 699
.pdf
|
|
kAe ak 2 sin k |
|
|
|
Ae ak 2 cos k , |
(3.13) |
|||
|
|
|
|
|
||||||
откуда после простейших преобразований получаем: |
|
|||||||||
|
|
|
ctg k |
|
|
k |
|
|
, |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
где |
|
= Bi. Если обозначить k |
= |
|
|
, то последнее выражение |
||||
можно записать следующим образом: |
|
|||||||||
|
|
|
ctg |
|
|
|
/ Bi . |
(3.14) |
||
|
y |
y1 = ctg |
y1 |
y1 |
|
|
y1 |
|
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
y2 = |
/Bi |
0 |
|
2 |
|
3 |
|
4 |
1 |
2 |
3 |
4 |
Рис. 3.3 К решению уравнения (3.14)
Из анализа этого тригонометрического уравнения следует, что при каждом значении Bi существует бесконечное множество решений. Наиболее просто уравнение (3.14) можно решить графическим способом.
Обозначим левую часть уравнения (3.14) через y1 = ctg , а правую - через y1 = /Bi. Пересечение котангенсоиды y1 с прямой y2 дает нам значение корней характеристического
198

уравнения, т. е. (рис. 3.3).
Из рис. 3.3 следует, что мы имеем бесконечное множест-
во значении величины |
n причем каждое последующее больше |
||
предыдущего: |
|
|
|
1 |
2 |
3 ... |
n ... |
Важно отметить, что каждому значению числа Bi отвечает своя совокупность корней уравнения (3.14).
198

Таблица 3.1
|
|
|
Значения n |
для пластины |
|
|
|
||||
Bi |
1 |
2 |
3 |
4 |
|
Bi |
1 |
|
2 |
3 |
4 |
0 |
0,0000 |
3,1416 |
6,2832 |
9,4248 |
|
1,0 |
0,8603 |
|
3,4256 |
6,4373 |
9,5293 |
0,001 |
0,0316 |
3,1419 |
6,2833 |
9,4249 |
|
1,5 |
0,9882 |
|
3,5422 |
6,5097 |
9,5801 |
0,002 |
0,0447 |
3,1422 |
6,2835 |
9,4250 |
|
2,0 |
1,0769 |
|
3,6436 |
6,5783 |
9,6296 |
0,004 |
0,0632 |
3,1429 |
6,2838 |
9,4252 |
|
3,0 |
1,1925 |
|
3,8088 |
6,7040 |
9,7240 |
0,006 |
0,0774 |
3,1435 |
6,2841 |
9,4254 |
|
4,0 |
1,2646 |
|
3,9352 |
6,8140 |
9,8119 |
0,008 |
0,0893 |
3,1441 |
6,2845 |
9,4256 |
|
5,0 |
1,3138 |
|
4,0336 |
6,9096 |
9,8928 |
0,01 |
0,0998 |
3,1448 |
6,2848 |
9,4258 |
|
6,0 |
1,3496 |
|
4,1116 |
6,9924 |
9,9667 |
0,02 |
0,1410 |
3,1469 |
6,2864 |
9,4269 |
|
7,0 |
1,3866 |
|
4,1746 |
7,0640 |
10,0339 |
0,04 |
0,1987 |
3,1543 |
6,2895 |
9,4290 |
|
8,0 |
1,3978 |
|
4,2264 |
7,1263 |
10,0949 |
0,06 |
0,2425 |
3,1606 |
6,2927 |
9,4311 |
|
9,0 |
1,4149 |
|
4,2694 |
7,1806 |
10,1502 |
0,08 |
0,2791 |
3,1668 |
6,2959 |
9,4333 |
|
10,0 |
1,4289 |
|
4,3058 |
7,2281 |
10,2003 |
0,1 |
0,3111 |
3,1731 |
6,2991 |
9,4354 |
|
15,0 |
1,4729 |
|
4,4255 |
7,3959 |
10,3898 |
0,2 |
0,4328 |
3,2039 |
6,3148 |
9,4459 |
|
20,0 |
1,4961 |
|
4,4915 |
7,4954 |
10,5117 |
0,3 |
0,5218 |
3,2341 |
6,3305 |
9,4565 |
|
30,0 |
1,5202 |
|
4,5615 |
7,3058 |
10,6543 |
0,4 |
0,5932 |
3,2636 |
6,3461 |
9,4670 |
|
40,0 |
1,2325 |
|
4,5979 |
7,6647 |
10,6334 |
0,5 |
0,6533 |
3,2923 |
6,3616 |
9,4775 |
|
50,0 |
1,5400 |
|
4,6202 |
7,7012 |
10,7832 |
0,6 |
0,7051 |
3,3204 |
6,3770 |
9,4879 |
|
60,0 |
1,5451 |
|
4,6353 |
7,7259 |
10,8172 |
0,7 |
0,7561 |
3,3477 |
6,3923 |
9,4983 |
|
80,0 |
1,5514 |
|
4,6543 |
7,7573 |
10,8606 |
0,8 |
0,7910 |
3,3744 |
6,4074 |
9,5087 |
|
100 |
1,5552 |
|
4,6658 |
7,7764 |
10,8871 |
0,9 |
0,8274 |
3,4003 |
6,4224 |
9,5190 |
|
|
1,5708 |
|
4,7124 |
7,8540 |
10,9956 |
Первые четыре корня уравнения (3.14) 1, 2, 3, и 4 приведены в табл. 3.1 для различных значений числа Bi (от 0 до ).
При Bi 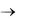 прямая y2 = /Bi совпадает с осью абсцисс и корни уравнения будут равны:
прямая y2 = /Bi совпадает с осью абсцисс и корни уравнения будут равны:
|
|
; |
|
3 |
; |
|
5 |
… , |
|
2n 1 |
|
. |
1 |
|
2 |
|
3 |
|
n |
|
|||||
|
|
|
|
|||||||||
2 |
|
2 |
|
2 |
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|||||
При Bi |
0 прямая y2 = |
/Bi совпадает с осью ординат и |
||||||||||
тангенс угла наклона прямой стремится к бесконечности, при этом корни уравнения (3.14) равны:
1 |
0 ; |
2 |
; |
3 |
2 … ; |
n |
n 1 , |
|
|
|
|
где n = 1, 2, 3 ...
Для других конечных значений числа Bi величины n имеют промежуточные значения (см. табл.3.1).
Следовательно, каждому найденному значению корня 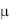 будет соответствовать свое частное распределение температуры:
будет соответствовать свое частное распределение температуры:
198
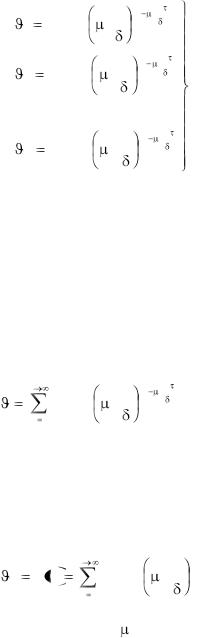
|
|
|
|
x |
2 a |
|
|
|
|
|||||
|
|
|
|
e 1 |
|
|
|
|
|
|||||
1 |
A1 cos |
1 |
|
|
2 ; |
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
|
2 a |
|
||||||
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
A 2 cos |
|
|
|
e |
2 ; |
|
|||||||
|
|
|
|
|
||||||||||
2 |
2 |
|
|
|
|
|
|
(3.15) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . . . . . . . |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
|
2 a |
|
|||||
|
|
|
|
|
|
|
n |
|
|
|
|
|||
|
A n cos |
|
|
|
|
e |
|
2 . |
|
|||||
|
|
|
|
|
|
|||||||||
n |
n |
|
|
|
|
|
|
|
||||||
Полученные частные решения (3.15) будут удовлетворять дифференциальному уравнению при любых значениях постоянных A1, A2, ... , An, но ни одно из этих решений не будет соответствовать действительному распределению температуры в начальный момент времени. Однако путем наложения бесконечного числа таких распределений при соответствующем выборе величин An можно воспроизвести любую действительную температурную зависимость в начальный момент времени.
На основании сказанного общее решение можно представить суммой бесконечного ряда:
n |
x |
|
2 |
a |
|
|
A n cos n |
e |
n |
2 . |
(3.16) |
||
|
|
|||||
n 1 |
|
|
|
|
|
|
Известно, что если отдельные распределения (3.15) удовлетворяют дифференциальному уравнению (3.4) и граничным условиям (3.6), то и сумма их также удовлетворяет тем же условиям.
Постоянная An в уравнении (3.16) найдется из начальных условий. Подчинив уравнение (3.16) начальному условию, получим:
|
n |
x |
|
|
|
0 F x |
A n cos n |
. |
(3.17) |
||
|
|||||
|
n 1 |
|
|
|
Уравнение (3.17) есть разложение четной функции в ряд Фурье с заданными параметрами n, определяемыми характе-
198

ристическим уравнением (3.14). Для этой последовательности чисел n справедлива формула
cos |
|
x |
cos |
|
x |
dx |
0 |
при n |
m, |
|
|
|
|
|
|
||||||
n |
m |
0 |
при n |
m, |
||||||
|
|
|
||||||||
|
|
|
|
|
|
|
||||
с помощью которой можно определить все коэффициенты An в уравнении (3.17). Для этого умножим обе части уравнения (3.17) на cos ( nx/ ) dx и затем проинтегрируем полученное соотношение по толщине пластины. Тогда
F x cos |
|
x |
dx A |
|
cos2 |
|
x |
dx , |
(3.18) |
n |
|
n |
n |
||||||
|
|
|
|
|
|
||||
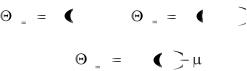
ибо все остальные слагаемые в правой части, для которых n 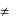 m, обращаются в нуль. Интеграл в правой части соотношения (3.18) равен
m, обращаются в нуль. Интеграл в правой части соотношения (3.18) равен
|
|
1 |
1 |
|
|
sin 2 n . |
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
n |
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
An |
|
n |
|
|
|
F x cos |
|
x |
dx . (3.19) |
|
sin n cos |
|
|
|
n |
||||
|
n |
n |
|
|
|
|
|
|
|
Из уравнения (3.19) следует, что An является функцией только корня характеристического уравнения и начального распределения температуры.
Подставив полученное выражение для постоянной An в уравнение (3.16), получим окончательное выражение для температурного поля при охлаждении однородной пластины:
n |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
n |
F x cos |
|
dx |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
sin n cos n |
n |
|
||||
|
|
|
|
|
|
|
||||
n 1 |
|
|
n |
|
|
|
(3.20) |
|||
|
|
|
|
|
a |
|
|
|
|
|
|
|
x |
|
2 |
|
|
|
|
||
cos |
|
e |
n |
2 . |
|
|
|
|
||
n |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
Уравнение (3.20) позволяет получить значение температуры в любой точке пластины для любого момента времени 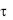
198

при любом начальном распределении температуры |
0. |
|
||||||
Если в начальный момент времени ( |
= 0) температура в |
|||||||
пластине распределена равномерно (рис. 3.2), т. е. t0 . tж = |
0 = |
|||||||
const, то интеграл в уравнении (3.19) равен ( 02 / |
n)sin |
n. С |
||||||
учетом сказанного выражение для постоянной An |
принимает |
|||||||
вид: |
|
|
|
|
|
|
|
|
A n |
|
|
2 sin |
n |
|
. |
(3.21) |
|
0 |
|
sin |
n cos |
|
||||
|
|
n |
n |
|
|
|||
Подставляя значение An, полученное для случая равномерного распределения температуры в пластине в начальный момент времени, в уравнение (3.20), получаем:
n |
0 2sin n |
|
|
|
x |
|
2 a |
|
|
|
|
|
|
cos |
n |
|
e |
n |
|
. |
(3.22) |
|
|
|
|
|
|
|||||
|
n sin n cos |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
n 1 |
n |
|
|
|
|
|
|
|
||
Уравнению |
температурного поля |
(3.22) |
целесообразно |
|||||||
придать безразмерную форму. Для этого разделим правую и
левую части уравнения (3.22) на |
0. При этом обозначим: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
A n |
D n . |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После этих преобразований получим: |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
n |
|
|
2sin |
|
|
|
|
|
x |
|
2 a |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
cos |
|
e |
n |
|
2 |
. |
(3.23) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
sin |
n cos |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0 |
|
n 1 |
n |
n |
|
|
|
|
|
|
|
|
|||||||||||
|
Входящие в уравнение температурного поля (3.23) вели- |
|||||||||||||||||||||||
чины |
|
|
; Dn; |
n; |
|
a |
; |
x |
являются безразмерными и имеют |
|||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следующий смысл:
0 = безразмерная температура; х/ = Х . безразмерная координата;
a / 2 = Fo - число Фурье, представляющее собой безразмерное время; Dn - безразмерный коэффициент.
С учетом последних обозначений уравнение (3.23) запишется:
129

n |
2 sin |
|
|
|
|
|
|
|
|
|
n |
|
cos |
|
X exp |
2 Fo |
. (3.24) |
||
|
|
|
|
n |
|||||
n 1 n sin |
n cos |
|
|
|
n |
|
|
||
n |
|
|
|
|
|
||||
Анализ полученного решения. Так как |
1, 2, |
3, …, |
n, |
||||||
представляет собой ряд возрастающих чисел, |
то чем больше |
, |
|||||||
тем меньше роль последующего члена ряда по сравнению с предыдущим. Кроме того, чем больше число Fo, тем члены ряда будут убывать быстрее с увеличением номера n.
Многочисленные исследования показали, что уже при Fo 0,3 ряд (3.24) становится настолько быстросходящимся, что распределение температуры достаточно точно описывается
первым членом ряда:
|
2 sin |
1 |
|
cos |
|
X exp |
2 Fo . |
(3.25) |
|
|
|
|
1 |
||||
|
1 sin |
1 cos |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
||
Ранее обозначено 2sin |
1/( |
1 + sin 1 cos 1) = D1. С уче- |
||||||
том этого обозначения уравнение (3.25) можно записать в следующем виде:
D1 cos 1X exp |
12 Fo . |
(3.25 ) |
Величина D1 является только функцией числа Bi и заранее может быть рассчитана и табулирована. Кроме того, если рассматривать температуру для определенного значения Х = х/ , то и cos ( 1Х) является функцией Bi. Конкретно для оси
пластины Х = х/ |
= 0 и cos ( 1 0) = 1, а для поверхности |
Х = х/ = 1 и cos ( |
1 1) = cos 1. |
Для оси пластины произведение D1cos(0) обозначим как некоторую функцию N(Bi). Тогда уравнение (3.25) можно за-
писать в следующем виде: |
|
X 0 N Bi exp 12 Fo . |
(3.26) |
Для поверхности 'пластины произведение D1cos |
1 обо- |
значим как некоторую функцию P(Bi) и уравнение (3.25 ) запишется так:
X 1 P Bi exp |
12 Fo . |
(3.27) |
Функции N(Bi) и P(Bi) в уравнениях (3.26) и (3.27) табулированы и для расчета могут быть взяты из справочников.
198
Кроме того, из уравнений (3.26) и (3.27) следует, что при заданной координате безразмерная температура является только функцией двух безразмерных параметров Bi и Fo:
X 0 f1 Bi, Fo и X 1 f2 Bi, Fo .
и X 1 f2 Bi, Fo .
Логарифмируя уравнение (3.26), получаем:
ln |
X 0 |
ln N Bi |
2 Fo . |
(3.28) |
|
|
1 |
|
Аналогичное уравнение может быть получено после логарифмирования уравнения (3.27).
Из уравнения (3.28) следует, что при заданном значении координаты и при заданном Bi натуральный логарифм безразмерной температуры линейно зависит от времени. Последнее обстоятельство дает возможность представить для уравнений (3.26) и (3.27) графическое решение (рис. 3.4 и 3.5).
198
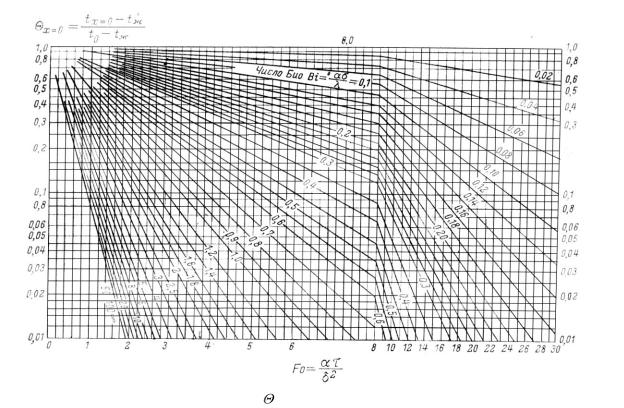
Рис. 3.4 Зависимость = f1 (Fo, Bi) для середины пластины
198

Рис. 3.5 Зависимость = f2 (Fo, Bi) для поверхности пластины
198
