
- •Линейная алгебра и аналитическая геометрия
- •Математический анализ.
- •1. Матрицы и действия над ними
- •2. Определители 2 ого и 3го порядка
- •3. Миноры и алгебраические дополнения.
- •4. Обратная матрица. Методы нахождения обратной матрицы
- •1. Метод присоединенной матрицы
- •2. Метод элементарных преобразований
- •5. Системы линейных алгебраических уравнений. Теорема Крамера.
- •6. Mетод Гаусса-Жордана.
- •7. Ранг матрицы. Теорема Кронекера – Капелли. Однородные системы линейных алгебраических уравнений
- •8. Линейная балансовая модель
- •9. Прямоугольная система координат в пространстве. Понятие вектора. Проекция вектора на ось. Направляющие косинусы вектора.
- •10. Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов.
- •11. Cкалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
- •12. Векторное произведение. Выражение векторного произведения через координаты векторов.
- •13. Смешанное произведение трех векторов. Выражение смешанного произведения через координаты векторов.
- •14. Векторное параметрическое уравнение прямой. Задача о делении отрезка в заданном отношении.
- •15. Координатные уравнения прямой в пространстве.
- •16. Координатные уравнения прямой на плоскости.
- •17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости.
- •18. Координатные уравнения плоскости.
- •19. Общие уравнения прямой в пространстве.
- •2 0. Взаимное расположение прямых и плоскостей в пространстве
- •21. Линии второго порядка( эллипс, гипербола, парабола)
- •22. Поверхности второго порядка
- •1. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций.
- •2. Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости)
- •4. Первый замечательный предел.
- •5.Второй замечательный предел.
- •6. Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы.
- •7. Непрерывность функции в точке. Классификация точек разрыва.
- •8. Основные теоремы о непрерывных функциях.
- •9. Понятия сложной и обратной функций.
- •10. Понятие производной. Геометрический и физический смыслы производной.
- •11. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.
- •12. Правила дифференцирования суммы, разности, произведения и частного.
- •13. Понятие дифференциала. Дифференциал суммы, разности, произведения и частного.
- •14. Производные постоянной, тригонометрических и логарифмической функций.
- •15. Производные обратной и сложной функций.
- •16. Производные показательной и обратных тригонометрических функций.
- •17. Логарифмическая производная. Производная степенной функции.
- •18. Таблица производных простейших элементарных функций.
- •19. Дифференцирование функции, заданной параметрически.
- •20. Теоремы Ферма и Ролля.
- •21. Теоремы Лагранжа и Коши.
- •22. Теорема Лопиталя.
- •23. Теорема Тейлора.
- •24. Признак монотонности. Необходимое условие локального экстремума. Достаточное условие локального экстремума.
- •25. Направление выпуклости и точки перегиба графика функции.
- •26. Необходимое условие наличия точки перегиба, достаточное условие наличия точки перегиба.
- •27. Асимптоты графика функции.
- •28. Комплексные числа и действия над ними.
- •29. Тригонометрическая форма комплексного числа.
- •30. Возведение комплексного числа в степень и извлечение корня. Формулы Эйлера.
- •Формулы
15. Координатные уравнения прямой в пространстве.
( 0,
е1,
е2,
е3)
– система координат точки А1(х1;у1;z1)
А2(х2;у2;z2)
Коорд.
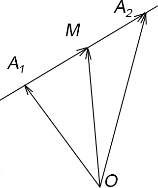
урав. прямой проходящей через А1А2:
ОМ=ОА1+tА1А2;
ОМ(х;у;z),
ОА1(х1;у1;z1),
А1А2(х2-х1;у2-у1;z2-z1)
→ А1А2(ax;ay;az)
Спроецируем
данное уравнение на оси координат: х=
х1+tax,
у= у1+taу,
z=
z1+taz
; параметрическое
уравнение прямой в пространстве:
0,
е1,
е2,
е3)
– система координат точки А1(х1;у1;z1)
А2(х2;у2;z2)
Коорд.
урав. прямой проходящей через А1А2:
ОМ=ОА1+tА1А2;
ОМ(х;у;z),
ОА1(х1;у1;z1),
А1А2(х2-х1;у2-у1;z2-z1)
→ А1А2(ax;ay;az)
Спроецируем
данное уравнение на оси координат: х=
х1+tax,
у= у1+taу,
z=
z1+taz
; параметрическое
уравнение прямой в пространстве:
 каноническое ур-ие;
каноническое ур-ие;
 ур-ие прямой в пространстве
ур-ие прямой в пространстве
t=


16. Координатные уравнения прямой на плоскости.
(0, е1, е2) – система координат точки А1(х1;у1) А2(х2;у2).
![]()
![]()
![]()
![]()
1.
Коорд.
параметр. уравнение прямой.
Используя векторное
параметр.
уравнение прямой можно получить два
скалярных, а именно: |
4. Общее уравнение прямой. Ax+By+C=0 ay(x-x1)=ax(y-y1) → ayx-axy+axy1-ayx1=0 (A=ay; B=-ax; C= axy1-ayx1) n(A;B) – нормальный вектор прямой |
2. Канонические уравнения.
|
3.
Уравнение прямой проходящей
через 2 точки.
А(х1;у1),
В(х2;у2)
|
5.
Ур-ие прямой с угловым коэффиц.
y=kx+b
Ax+By+C=0→ |
6. Нормированное (нормальное) уравнение прямой. x cos +y sin -p=0; r(x;y) n(cos ;sin ); r•n=p → (x;y)( cos ;sin )=OP → x cos +y sin =OP |
7.
Уравнение прямой в отрезках на осях.
|
8.
Уравнение прямой проходящей через
точку заданной угловым коэфф.
y-y1=k(x-x1)
M1(x1;y1)
k=tg
при
|| +k1=k2
при
k1= |

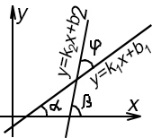
17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости.

В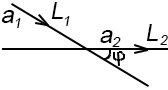 заимное
расположение прямых на плоскости:
условие
|| : y=k1x+b1
; y=k2x+b2
; k1=k2
заимное
расположение прямых на плоскости:
условие
|| : y=k1x+b1
; y=k2x+b2
; k1=k2
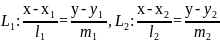 ; a1=(l1;m1),
a2=(
l2;m2)
; a1=(l1;m1),
a2=(
l2;m2)
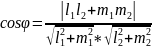 –
формула
угла между прямыми
–
формула
угла между прямыми
Если
L1
||
L2,
то
|
Если
L1 |
|
|
18. Координатные уравнения плоскости.
Пусть в пространстве задана плоскость и точка соответствующая координатам М1(х1; у1; z1) А(х-х1)+В(у-у1)+С(z-z1)=0 A2+B2+C2 0(одновременно не обращаются) Расммотрим 2 точки, принадлежащие плоскости М2(x2;у2;z2) и М3(х3;у3; z3) и векторы соответственно М1М, М1М2, М1М3 М(х; у; z) – произвольная точка на плоскости М тогда и только тогда принадлежт плоскости, когда эти векторы – коллинеарны
М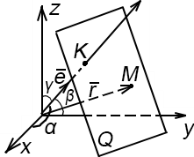 1М•М1М2•М1М3=
1М•М1М2•М1М3= A(х-х1)+B(у-у1)+C(z-z1)=0
уравнение
плоскости, проходящей через 3
точки
A(х-х1)+B(у-у1)+C(z-z1)=0
уравнение
плоскости, проходящей через 3
точки
 Ax+By+Cz+D=0
– общее уравнение плоскости
Ax+By+Cz+D=0
– общее уравнение плоскости
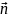 (А;
В;С) – нормальный вектор плоскости
(вектор нормали)
Нормальное
уравнение плоскости.
ОК
(Q);
OK=p;
M(x;y;z);
α,β,γ – углы, обр. единым вектором е
с
осями Ох, Оу, Oz.
Тогда е=(cos
α;cos β; cos
γ), r
= OM=(x;y;z)
При
любом положении точки М на плоск. Q
проекция радиус-
вектора r
на направление вектора e
всегда равно p:
преr=p
r•e-p=0
-
нормальное уравнение плоскости в
векторном виде
x•cosα
+ y•cosβ + z•cosγ
– p
= 0
нормальное уравнение плоскости в
координатном виде
(А;
В;С) – нормальный вектор плоскости
(вектор нормали)
Нормальное
уравнение плоскости.
ОК
(Q);
OK=p;
M(x;y;z);
α,β,γ – углы, обр. единым вектором е
с
осями Ох, Оу, Oz.
Тогда е=(cos
α;cos β; cos
γ), r
= OM=(x;y;z)
При
любом положении точки М на плоск. Q
проекция радиус-
вектора r
на направление вектора e
всегда равно p:
преr=p
r•e-p=0
-
нормальное уравнение плоскости в
векторном виде
x•cosα
+ y•cosβ + z•cosγ
– p
= 0
нормальное уравнение плоскости в
координатном виде

 a(ax;ay)
– направляющий вектор прямой
a(ax;ay)
– направляющий вектор прямой (l;m)
– направляющий косинусы прямой
(l;m)
– направляющий косинусы прямой
 k=tg
k=tg b
– точка перес. прямой и Оу до (0;0)
b
– точка перес. прямой и Оу до (0;0)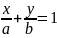 Ax+By+C=0
→
Ax+By+C=0
→ →
→
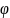 =0
и tg
=0;
k1=k2→
условием паралел. двух прямых явл.
равенство коэф. k1=k2
=0
и tg
=0;
k1=k2→
условием паралел. двух прямых явл.
равенство коэф. k1=k2
 L2,
то
=
L2,
то
= ; сtg
=
; сtg
= = 0; получ. 1+ k1k2
=0→ k1k2=-1
→ условием перпенд. прямых явл.
равенство k1k2=-1
или k1=
= 0; получ. 1+ k1k2
=0→ k1k2=-1
→ условием перпенд. прямых явл.
равенство k1k2=-1
или k1=