22. Теорема Лопиталя.
f(x), g(x) определены в некоторой окрестности за исключением может быть самой точки и удовлетворяет условиям 1) f(x) и g(x)-дифференцируемы
2)
g´(x)
0,
то существует формула
и
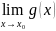3)
справедлива формула
=
=
=
;
=
=
Пример:
=
=
=
=
;
=
=
=
...=
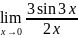=0
3)
=
=
=
=
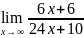23. Теорема Тейлора.
Если
f(x)
имеет в некоторой окрестности точку
,
производную (n+1)
порядка, существует
окр.
,
f(x)=
+
(x),
где
(x)=
*
Пример:
Найти
формулу Тейлора для функции у=
при
=0.
y´=
;
y´(0)=1;
=
;
;
=
+
;
=
+
;
=1+
+
+
...+
+
(x).
24. Признак монотонности. Необходимое условие локального экстремума. Достаточное условие локального экстремума.
Строгий локальный экстремум (max\min) – точка х=х0 называется точкой локального максимума или минимума функции y=f(x), если существует окрестность этой точки такая, что для любых х из этой окрестности выполняется: f(x)<f(x0)(f(x)>f(x0)
ВСТАВИТЬ РИСУНКИ СО СТРАНИЦЫ 131
Если
функция f(х)
диф. на интервале (a;b)
и f´(x)≥0
(f(x)≤0)
для любых х
(a;b),
то функция не убывает(не возрастает) на
этом интервале.
Доказательство: на
интервале (a;b)
выполнены все условия теоремы Лагранжа
для любых
,
, f(a;b);
.
f(
)-f(
=f´(C)(
;f´(C)≥0,(
;C
;
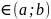f(
)-f(
)≥0
следовательно f(
≥f(
Функция не убывающая, ч.т.д. Т(
,f(
-называется
точкой локального max(min),
если существует ∆-окрестность в точки
такая, что для любых х из этой окрестности
выполняется неравенство f(
)
Необходимое
условие локального экстремума. Если
f(x)
имеет в точке
локальный экстремум и диф. в этой точке,
то f´(
)=0.
Доказательство данной теоремы основано
на теореме Ферма. Пример:y=
;y´(x)=3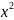
;
3
=0;
x=0.
Достаточное
условие локального экстремума:
Если f(x)
диф. в некоторой окрестности точки
и опр. в ней, то
1)
f´(x)
)
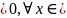- Max
f´(x)
2)
f´(x)
)
- Min
f´(x)
Доказательство основано на теореме Лагранжа.
y=
25. Направление выпуклости и точки перегиба графика функции.
Если
функция f(x)
имеет на (a;b)
вторую производную и f´´(x)
0
(f´´(x)
0)
,
то график функции имеет выпуклость
направленную вниз(вверх). Доказательство
Запишем уравнение касательной R
в точке
;
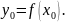y=f(
уравнение
касательной. Рассмотрим интервал (a;b)
на нёразложим по формуле Тейлора
y=f(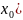
+
(x-
+
;
;
Y-y=
;
y-Y
;
y-Y
,
y
Точки
перегиба графика функции:(
)
называется точкой перегиба графика
функции y=f(x),
если график имеет в этой точке касательную
и разные напр. выпуклости слева и справа
от этой точки.
26. Необходимое условие наличия точки перегиба, достаточное условие наличия точки перегиба.
Если функция y=f(x) имеет в точке перегиб и непрерывную производную в некоторой окрестности этой точки, то вторая производная в этой точке равна 0. Доказательство: производится от обратного предположения, что вторая производная не равна 0. По теореме о сохранение знака сущ. окрестность, в которой функция имеет тот же знак, что и в точке , а это противоречит условию теоремы. Достаточное условие точки перегиба: для того чтобы имела в точке перегиб, достаточно, чтобы она имела f´´ и разные направления выпуклости слева и справа от этой точки.
27. Асимптоты графика функции.
Асимптоты-
прямая, к которой график функции сколь
угодно раз близко приближается при х
или
в окрестности точек разрыва. Асимптоты
бывают: вертикальными, горизонтальными,
наклонными. Горизонтальная асимптота:
прямая у=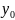
графика f(х)
если
.
Прямая х=
называется вертикальной асимптотой
графика у=f(х),
если хотя бы один из односторонних
пределов
.
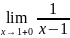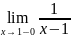у=
=+
;
=-
.
у=
;
=
=0, у=0- горизонтальная асимптота.
.
Наклонная асимптота- это прямая у=kx+b
график функции у=f(x)
при f(x)=kx+b+
,
x
,
где
k=
;
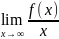b=
.
Если хотя бы один из пределов не существует
или бесконечен, то наклонной асимптоты
нет. Пример:
y=
;
k=
;
у=
=
=
=1
y=1*x+1=x+1
Cхема
исследования графика функции. 1)Область
определения, область значения, чётность,
не чётность, периодичность.2)Характерные
точки графика функции(пересечение с
осями)- х=0,у=0. 3)Точки
возможного экстремума. f´(x)=0
. Интервалы монотонности f´(x)
,
f´(x)
4)Точки
перегиба:f´´(x)=.0
Направление выпуклости f´´(x)
;
f´´(x)˂0.
5)Асимптоты
графика функции 6)
Построение графика на основании
исследования.