9.​ Понятия сложной и обратной функций.

Пусть даны две функции z = f(y) и  у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)).

Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную  у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи  g обозначает функцию, обратную к f. Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями.

Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат –их значения, то эти графики будут симметричны друг другу относительно прямой  у = х

10.​ Понятие производной. Геометрический и физический смыслы производной.

Производной функции у=f(х) в т. Х₀ называется предел отношения приращения ф-ции в этой точке к приращению аргумента при ∆х→0, т.е.

Геометрический смысл: производная в т. Х₀ равна угловому коэффициенту касательной к графику функции у=f(x) в этой точке f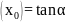

Уравнение касательной к графику функции y=f(x) в т. Х₀: y= f(x₀) + f ^‘(x₀)(x-x₀)

Физический смысл производной: производная функции у=f(х) в точке Х₀ – это скорость изменения функции f(х) в т. Х₀: V(t)=x'(t)

11.​ Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.

Функция у=f(х) называется дифференцируемой в точке х₀, если ее приращение в этой точке можно представить в виде: ∆у=А∆х+0(∆х), где А- некоторая постоянная, а 0(∆х) – является бесконечно малой величиной при ∆х→0.

Теорема о дифференцируемости: Для того чтобы функция у=f(x) была дифференцируема в т. Х₀, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Cвязь между понятиями дифференцируемости и непрерывности. Имеет место следующая теорема. Если функция y=f(x) дифференцируема в точке х₀, то она непрерывна в этой точке. Доказательство. Так как функция y=f(x) дифференцируема в точке x₀, то существует конечный предел . Тогда по теореме о связи бесконечно малой величины с функцией, имеющей конечный предел, будем иметь , где a(∆x) - бесконечно малая величина при ∆x→ 0 .

Откуда ∆y=f '(x₀)∆x + a(∆x)*∆x

Переходя в этой формуле к пределу при ∆х→0, получим по свойствам бесконечно малых, что

Следовательно, по одному из определений непрерывности функция y=f(x) в точке x₀ является непрерывной. Обратная теорема, вообще говоря, неверна, т.е. функция может быть непрерывной в данной точке, но не быть дифференцируемой в этой точке.

12.​ Правила дифференцирования суммы, разности, произведения и частного.

Если существуют производные U'(x) и V'(x), то производная от суммы(разности) этих функций равна сумме (разности) производных:

(u(x)±v(x))’=u’(x) ± v’(x)

Правило дифференцирования суммы или разности функций также следует из определения производной функции и свойства пределов функций, согласно которому предел суммы (или разности) функций равен сумме (или разности) соответствующих пределов.

Если существуют производные U'(x) и V'(x), то выполняются следующие правила дифференцирования произведения функций и частного от их деления: (U*V)'=U'V+ UV'; (