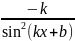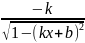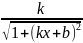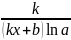- •Линейная алгебра и аналитическая геометрия
- •Математический анализ.
- •1. Матрицы и действия над ними
- •2. Определители 2 ого и 3го порядка
- •3. Миноры и алгебраические дополнения.
- •4. Обратная матрица. Методы нахождения обратной матрицы
- •1. Метод присоединенной матрицы
- •2. Метод элементарных преобразований
- •5. Системы линейных алгебраических уравнений. Теорема Крамера.
- •6. Mетод Гаусса-Жордана.
- •7. Ранг матрицы. Теорема Кронекера – Капелли. Однородные системы линейных алгебраических уравнений
- •8. Линейная балансовая модель
- •9. Прямоугольная система координат в пространстве. Понятие вектора. Проекция вектора на ось. Направляющие косинусы вектора.
- •10. Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов.
- •11. Cкалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
- •12. Векторное произведение. Выражение векторного произведения через координаты векторов.
- •13. Смешанное произведение трех векторов. Выражение смешанного произведения через координаты векторов.
- •14. Векторное параметрическое уравнение прямой. Задача о делении отрезка в заданном отношении.
- •15. Координатные уравнения прямой в пространстве.
- •16. Координатные уравнения прямой на плоскости.
- •17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости.
- •18. Координатные уравнения плоскости.
- •19. Общие уравнения прямой в пространстве.
- •2 0. Взаимное расположение прямых и плоскостей в пространстве
- •21. Линии второго порядка( эллипс, гипербола, парабола)
- •22. Поверхности второго порядка
- •1. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций.
- •2. Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости)
- •4. Первый замечательный предел.
- •5.Второй замечательный предел.
- •6. Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы.
- •7. Непрерывность функции в точке. Классификация точек разрыва.
- •8. Основные теоремы о непрерывных функциях.
- •9. Понятия сложной и обратной функций.
- •10. Понятие производной. Геометрический и физический смыслы производной.
- •11. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.
- •12. Правила дифференцирования суммы, разности, произведения и частного.
- •13. Понятие дифференциала. Дифференциал суммы, разности, произведения и частного.
- •14. Производные постоянной, тригонометрических и логарифмической функций.
- •15. Производные обратной и сложной функций.
- •16. Производные показательной и обратных тригонометрических функций.
- •17. Логарифмическая производная. Производная степенной функции.
- •18. Таблица производных простейших элементарных функций.
- •19. Дифференцирование функции, заданной параметрически.
- •20. Теоремы Ферма и Ролля.
- •21. Теоремы Лагранжа и Коши.
- •22. Теорема Лопиталя.
- •23. Теорема Тейлора.
- •24. Признак монотонности. Необходимое условие локального экстремума. Достаточное условие локального экстремума.
- •25. Направление выпуклости и точки перегиба графика функции.
- •26. Необходимое условие наличия точки перегиба, достаточное условие наличия точки перегиба.
- •27. Асимптоты графика функции.
- •28. Комплексные числа и действия над ними.
- •29. Тригонометрическая форма комплексного числа.
- •30. Возведение комплексного числа в степень и извлечение корня. Формулы Эйлера.
- •Формулы
18. Таблица производных простейших элементарных функций.
f(kx+b) |
f’(kx+b) |
ctg(kx+b) |
|
(kx+b)p |
kp(kx+b)p-1 |
arcsin(kx+b) |
|
ekx+b |
kekx+b |
arccos(kx+b) |
|
akx+b |
kakx+blna |
arctg(kx+b) |
|
ln(kx+b) |
|
arcctg(kx+b) |
|
loga(kx+b) |
|
sh x |
ch x |
sin(kx+b) |
k cos(kx+b |
ch x |
sh x |
cos(kx+b) |
-k sin(kx+b) |
th x |
|
tg(kx+b) |
|
cth x |
|
19. Дифференцирование функции, заданной параметрически.
Рассмотрим
функции, заданные параметрическими
уравнениями:
x=ϕ(t),
y=Ψ (t);
t

Параметрически заданную функцию можно рассматривать как сложную:
х=ϕ(t)
; t= (x)
; (
(x)≠0)
(x)
; (
(x)≠0)
y=Ψ (t) =Ψ( (x))
y'=Ψ' (t) (
(x))'=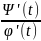 формула
производной параметрически заданной
функции:
формула
производной параметрически заданной
функции:
y'=
20. Теоремы Ферма и Ролля.
Т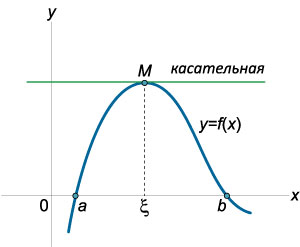
![]() еорема
Ферма. Пусть
f(x)
задана на открытом промежутке и достигает
в
своего max(min),
тогда если f(x)
имеет f´(x),
то она равна 0.
Доказательство:
Допустим
еорема
Ферма. Пусть
f(x)
задана на открытом промежутке и достигает
в
своего max(min),
тогда если f(x)
имеет f´(x),
то она равна 0.
Доказательство:
Допустим
 точка maх;
f´(
)=
точка maх;
f´(
)= ∆f=(f(
+∆x)-f(
))≤0
+ ∆x
1
∆f=(f(
+∆x)-f(
))≤0
+ ∆x
1![]() )∆x
)∆x 0
∆f
˂0 следовательно
0
∆f
˂0 следовательно
 ˂
0
˂
0
 =f´(x)
≤ 0 2)∆x˂0
∆f
0
следовательно
=f´(x)
≤ 0 2)∆x˂0
∆f
0
следовательно
 0
=f´(x)
0
=f´(x) 0
Из этих условий следует, что f´(x)=0
Теорема
Ролля.
Если
функция f(x)
непрерывна на отрезке
0
Из этих условий следует, что f´(x)=0
Теорема
Ролля.
Если
функция f(x)
непрерывна на отрезке
 ,
дифференцируема во всех точках интервала
(a;b)
и на концах x=a
и x=b
принимает равные значения (f(a)=f(b)),
то существует внутри интервала (a;b)
по крайней мере одна точка x=c
, a˂c˂b,
в которой производная f´(х)
обращается в ноль, т.е. f´(с)=0
Доказательство
:
Рассмотрим
два случая: 1)Если
непрерывна на
,
то по второй теореме Вейерштрасса.
М-наиб. m-наим.
M=m
следовательно f(x)-const.
F´(x)=0,
x
,
дифференцируема во всех точках интервала
(a;b)
и на концах x=a
и x=b
принимает равные значения (f(a)=f(b)),
то существует внутри интервала (a;b)
по крайней мере одна точка x=c
, a˂c˂b,
в которой производная f´(х)
обращается в ноль, т.е. f´(с)=0
Доказательство
:
Рассмотрим
два случая: 1)Если
непрерывна на
,
то по второй теореме Вейерштрасса.
М-наиб. m-наим.
M=m
следовательно f(x)-const.
F´(x)=0,
x (a;b)
2)Если m˂M
то хотя бы одно из значений функции
достигает внутри промежутка. Значит
это локальный экстремум. Следовательно
по теореме Ферма f´(c)=0Теорема
Ролля имеет наглядный физический смысл.
Предположим, что тело движется вдоль
прямой и через некоторый промежуток
времени возвращается в исходную точку.
Тогда в данном промежутке времени
существует момент, в котором мгновенная
скорость тела была равна нулю.
(a;b)
2)Если m˂M
то хотя бы одно из значений функции
достигает внутри промежутка. Значит
это локальный экстремум. Следовательно
по теореме Ферма f´(c)=0Теорема
Ролля имеет наглядный физический смысл.
Предположим, что тело движется вдоль
прямой и через некоторый промежуток
времени возвращается в исходную точку.
Тогда в данном промежутке времени
существует момент, в котором мгновенная
скорость тела была равна нулю.
21. Теоремы Лагранжа и Коши.
Теорема
Лагранжа:
Если функция f(x)
удовлетворяет условиям:
1. Функция
непрерывна на
2. Функция дифференцируема на
 3. Производная функции не равна 0, х
принадлежит (а; в) -> то существует
3. Производная функции не равна 0, х
принадлежит (а; в) -> то существует
 (a;b)
такая что f(b)-f(a)=f´(
(a;b)
такая что f(b)-f(a)=f´( )*(b-a)
Доказательство:
Рассмотрим
вспомогательную функцию
)*(b-a)
Доказательство:
Рассмотрим
вспомогательную функцию

Эта функция непрерывна и дифференцируема в промежутке [a;b], а на его концах принимает одинаковые значения: F(a)=F(b)=0
Тогда F(x) удовлетворяет всем условиям теоремы Ролля и, следовательно, существует точка (a;b), в которой производная функции F(x) равна нулю:

геометрический смысл: геометрический смысл теоремы Лагранжа таков: на графике функции f(x) найдется точка С(с, f(с)), в которой касательная к графику f(x) параллельна секущей АВ. Следствия:1. Если f'(х) = 0 на некотором промежутке (a, b), то функция f(x) постоянна на этом промежутке.2.Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Теорема
Коши:
Если
1) f(x)
и g(x)
непрерывны на
2) f(x)
и
g(x)
дифференцируемы на (a;b)
3) g´(x)
0
на
.
то существует точка С такая что
такая что
 =
= .
Следствие: теорема Лагранжа является
частным случаем теоремы Коши при g(x)=x.
.
Следствие: теорема Лагранжа является
частным случаем теоремы Коши при g(x)=x.