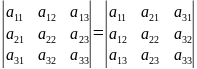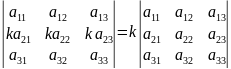- •1. Матрицы и действия над ними.
- •2. Определители второго и третьего порядков.
- •3. Миноры и алгебраические дополнения.
- •4. Обратная матрица.
- •5. Решение систем линейных алгебр. Уравнений. Теорема Крамера.
- •6. Линейная балансовая модель Леонтьева.
- •7. Метод Гаусса-Жордана.
- •8. Ранг матрицы. Теорема Кронекера-Капелли.
- •9. Прямоугольная система координат в пространстве. Понятие вектор. Проекция вектора на ось. Направляющие косинусы вектора.
- •10. Линейные операции над векторами. Теоремы о проекциях векторов. Линейная зависимость векторов.
- •11. Скалярное произведение векторов. Выражение скалярного произведения через координаты векторов.
- •12. Векторное произведение. Выражение векторного произведения через координаты векторов.
- •13. Смешанное произведение трех векторов. Выражение смешанного произведения через координаты векторов.
- •14. Векторное параметрическое уравнение прямой. Задача о делении отрезка в зад. Отношении.
- •1 5. Координатные уравнения прямой в пространстве.
- •16. Координатные уравнения прямой на плоскости.
- •17. Угол между двумя прямыми. Взаимное расположение прямых на плоскости.
- •18. Координатные уравнения плоскости.
- •19. Общие уравнения прямой в пространстве.
- •2 0. Взаимное расположение прямых и плоскостей в пространстве
- •22. Поверхность второго порядка
- •1. Множества. Грани числовых множеств. Абсолютная величина числа. Понятие функции. Классификация функций.
- •2.Предел последовательности. Понятие сходящейся последовательности. Теоремы о сходящихся последовательностях (единственный предел, необходимое условие сходимости)
- •4.Первый замечательный предел.
- •5.Второй замечательный предел.
- •6.Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы.
- •7.Непрерывность функции в точке. Классификация точек разрыва.
- •8.Основные теоремы о непрерывных функциях.
- •9.Понятия сложной и обратной функций.
- •10. Понятие производной. Геометрический и физический смыслы производной.
- •11. Понятие дифференцируемости функции. Связь между понятиями дифференцируемости и непрерывности.
- •12. Правила дифференцирования суммы, разности, произведения и частного.
- •13. Понятие дифференциала. Дифференциал суммы, разности, произведения и частного.
- •14. Производные постоянной, тригонометрических и логарифмической функций.
- •15. Производные обратной и сложной функций
- •16. Производные показательной и обратных тригонометрических функций.
- •17. Логарифмическая производная. Производная степенной функции.
- •18. Таблица производных простейших элементарных функций.
- •19. Дифференцирование функции, заданной параметрически.
- •20. Теоремы Ферма и Ролля.
- •21. Теорема Лагранжа и Коши.
- •22. Теорема Лопиталя.
- •23. Теорема Тейлора.
- •24. Признак монотонности.
- •25. Направление выпуклости.
- •26. Необходимые условия точки перегиба.
- •27. Асимптоты графика функции.
- •28. Комплексные числа.
- •29. Тригонометрическая форма комплексного числа.
- •30. Возведение комплексного числа в степень и извлечение корня.
1. Матрицы и действия над ними.
Основные понятия. Матрица – прямоугольная таблица чисел, составленная из некоторых математических объектов, состоящая из m строк и n столбцов. i (m) – номер строки; j (n) – номер столбца Матрицы спец. вида:
квадратная |
единичная |
диагональная |
матрица строка |
матрица столбец |
ступенчатая |
|
|
|
|
|
|
Действие над матрицами.
1.
Сложение: суммой двух матриц A
и B
называется матрица С, такая, что
 2.
Умножение
на число: произвед. матрицы Amxn=(aij)
на число k
наз. матрица Bmxn=(bij)
такая, что bij=k*aij
2.
Умножение
на число: произвед. матрицы Amxn=(aij)
на число k
наз. матрица Bmxn=(bij)
такая, что bij=k*aij
 Обладает
свойствами: коммутативность [a+b=b+a],
ассоциативность [a+(b+c)=(a+b)+c],
дистрибутивности [a(b+c)=ab+ac]
кольцо-
это множество сведенных на нем операций
не слож. и выч.
алгебр.
структура
– множество сведенных на нем хотя бы
одной операции
линейным
пространством наз.
множ-во сведенное опер. умножение,
сложение на число
3.
Произведение
матриц: А*В наз. такая матрица С, каждый
элемент сij
которой
равен
Обладает
свойствами: коммутативность [a+b=b+a],
ассоциативность [a+(b+c)=(a+b)+c],
дистрибутивности [a(b+c)=ab+ac]
кольцо-
это множество сведенных на нем операций
не слож. и выч.
алгебр.
структура
– множество сведенных на нем хотя бы
одной операции
линейным
пространством наз.
множ-во сведенное опер. умножение,
сложение на число
3.
Произведение
матриц: А*В наз. такая матрица С, каждый
элемент сij
которой
равен
сумме
произведений элементов i-й
строки матрицы А на соответствующие
элементы j-го
столбца матрицы В: (Аmxn;
Bcxb;
n=c;
A*B=Cmxb)
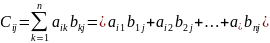 пример:
пример:
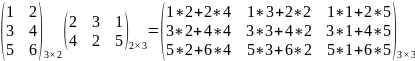 А*В
А*В В*А
В*А
4.
Транспонирование: матрица Ат
наз.
транспонир., если атij
=
aji
Amxn;
Атnxm
пример:

2. Определители второго и третьего порядков.
Квадратной матрице А порядка n можно составить число detA (или |A|, или ∆), наз. ее определители след. образом:
1. n=1; A=(a1); detA=a1 2.
n=2; A= |
3. n=3; A= ; |
свойства:
1.
Определитель не изменится, если его
строки заменить столбцами и наоборот
пример:
|
2.
При перестановке двух парал. рядов
определитель меняет знак:
пример:
|
|
n3.
Определитель, имеющий два одинаковых
ряда равен нулю
пример:
|
4.
Если в определителе две строки
пропорц., то определитель равен нулю.
пример:
|
|
5. Если в определителе сумме двух слагаемых, то определитель равен сумме всех определителей пример:
|
||
6. Если какая-либо строка в опред. содержит общий множитель, то его можно вынести за знак определителя пример: в 4 свойстве |
||
7.
Определитель не изменится, если к
элементам одного ряда прибавить
соответствующие элементы параллельного
ряда, умнож. на любое число
пример:

Теория Лапласа |
|
3. Миноры и алгебраические дополнения.
Минором (Mij) некоторого элемента аij определителя n-го порядка наз. определитель n-1-го порядка, полученный из исходного путем вычеркивания |
|
строки и столбца на пересечении некоторых находится выбранный элемент.
Алгебраическим дополнением (Аij) элемента aij определителя наз. его минор, взятый со знаком «плюс», если сумме i+j – четное число, и со знаком «минус», если эта сумма нечетная. Аij=(-1)i+j Mij detA = ak1j Ak1j + ak2j Ak2j + ak3j Ak3j






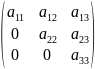
 ;
|A|=a11*a22
−
a12*a21
;
|A|=a11*a22
−
a12*a21