Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2216

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

4.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

Проделаем следующие операции:
1. Разбиваем область	V на n участков объемами i	и
диаметрами di , d maxdi	примем за параметр разбиения.
2. На любых участке выбираем произвольную точку Pi xi, yi
и составляем интегральную сумму:

f Pi i .

3.Перейдем к пределу этой суммы при условии, что n и

d 0.

Определение. Если предел существует и не зависит ни от способа разбиения области V на участки, ни от выбора точек Pi ,

называется тройным интегралом

		def	n	n	i	i	i	i
	f x, y,z dxdydz		n		i	i	i	i
	f x, y,z dxdydz		lim		f x	, y	,z
V			d 0	i 1

(1)

def : f x, y,z d	или f x, y,z dxdydz.
V	V

Определение. Пространственная область V называется правильной в направлении оси Oz, если координаты любых точек этой области удовлетворяют системе неравенств (рис.2):

a x b;
			x y			x ;
			x y		2	x ;
	1				2
				x, y z				x, y .
		1		x, y z			2	x, y .
		1					2

	z	z2 2 x, y
		z1 1 x, y
	0	y
	a	y
	x
	b	y 2 x
x	y 1 x	y 2 x

Рис. 2

Т е о р е м а. Тройной интеграл по правильной области сводится к трехкратному интегрированию формулой

	b	2 x 2 x
f x, y,z dxdydz dx		dy	f x, y,z dz.
V	a	1 x	1 x
(2)
Без доказательства.
Пример.
Вычислить f x, y,z dxdydz,			где	V	– область,
V
ограниченная цилиндром y x2	и плоскостью			z 0,	y z 1 0,
y z 1 (рис.3, а), б), в)).

1 x 1;

V: x2 y 1; D0 z 1 y.

1 1 y

f z xy dxdydz dx dy z xy dz

1 x2

z	б)	y
а)	б)	1
		1

																																										1		0								1					x
																																						в)						z
																0																y						в)
																0																y																									y
																																																									y
				x																										Рис. 3																0											x





						1		1				z		2							1 y						1						1						2
												z																							1 y
													2																						2
							dx			dy							xyz												dx											xy 1 y									dy

						1		x2													0	1				1						x2							1 x
1					1 y			3				y			2					y	3	1									1					x						2	3		x			5			x			7
					1 y							y								y													x			x									x						x
										x								x							dx																															dx
							6			x			2					x		3					dx															6						2						3				dx
							6						2							3				2										2 3						6						2						3
1																							x	2
1																							x							1
	1 x						1			x2				x		4			x6				x5					x7								x2					x		x3				x5						x		7
																																dx
																																dx
			6 6 2												2					6		2							3								12 6 6 10 42
1									x8 1
						x6			x8 1									2 2 2									2							16		0,15.


						12		24			1							6 6 10 42 105
		Замена переменных в тройном интеграле.
		Рассмотрим															f x, y,z dxdydz																					и			сделаем									замену

переменных по формулам:

x x , , ;

y y , , ;z z , , .

(3)

Якобиан этой замены суть определитель 3-го порядка:

x	x	x

y	y	y	.
			.

z	z	z

(4)

Т е о р е м а. Если в области V Якобиан 0, то имеет место

следующая формула замены переменных:

f x,y,z dxdydz f * , ,

d d d ,

(5)

где V * – область V в новых координатах; f *

– функция f

учетом формул (3). Без доказательства.

Тройной интеграл в цилиндрических координатах.

Рис. 4

def

M OM xi y j zk M x, y,z .

Пусть ПрOxyM P,

M , ,z

;

OPOx ;

–

цилиндрические координаты;

0 2 ;

z (рис.

4).

Формулы перехода:

x cos ;

y sin ;

z z.

(6)

Якобиан замены переменных (6):

cos

sin

cos

В силу формулы (5) имеем тройной интеграл в цилиндрических координатах:

	f x, y,z dxdydz f * , ,z d d dz			.
(7)	V		V*
(7)
Пример.
Вычислить тройной интеграл x2 y2 dxdydz;V –					часть
цилиндра x2 y2			V
цилиндра x2 y2		1,	ограниченного плоскостями z 0,		z 1.

ПрOxyV D (рис. 5, а), б)).

z	б)
а)	б)	y
		y
		1	D
V			x
V
0	1	0	1
0		1
y		1

Рис. 5

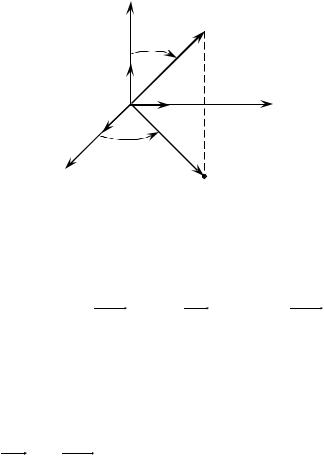
0 2 ;

V*: 0 1;

0 z 1.

x2 y2 dxdydz 2 cos2 2 sin2 d d dz

V		V*				1
	2	1	1		4	1
					4
3 d d dz d			3 d dz 2					.
3 d d dz d			3 d dz 2	4				.
V*	0	0	0	4		0	2

Тройной интеграл в сферических координатах.

zM (x, y ,z)

Рис. 6

M x, y,z – декартовы координаты.

Пусть ПрOxyM P,

R; OPOX ;

OM OZ .

M R, , – сферические

R 0;

координаты (рис. 6).

0 2 ;

0 , т.е.

всегда

рассматривается

в полуплоскости

OZ,M .

Формулы перехода:

Так как

cos

Rsin , и

пользуясь

формулами (3), имеем:

x Rsin cos ;

y Rsin sin ; R2 sin 0.

z Rcos ;

(8)

sin cos

Rcos cos

Rsin sin

sin sin

Rcos sin

Rsin cos

cos

Rsin

cos cos

sin sin

R2 cos

cos sin

sin cos

sin

sin cos

sin sin

sin cos

R2 sin cos2 sin3 R2 sin .

Всилу формул (5) имеем тройной интеграл в сферических координатах:

f x, y,z dxdydz f * R, , R2 sin dRd d .

V	V*
(9)
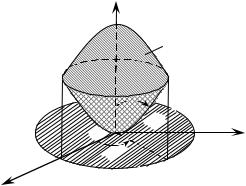
Пример.	z dxdydz, где
Вычислить	z dxdydz, где	– шаровой		сектор,
	V
ограниченный сферой x2 y2 z2 1		и конусом x2 y2		z2	0.
Образующая конуса составляет с осью Oz углы в			(рис.7).
Образующая конуса составляет с осью Oz углы в			(рис.7).
		4

				0	y
		x			y
		x
				Рис. 7
Так	как	x 0;		y z	–	биссектриса
Так	как		2 z2	y z	–	биссектриса
		x2 y	2 z2	0;

координатных углов.

0 R 1;


*: 0		;
*: 0	4	;
	4

0 2 .

Согласно формулам (8), (9) имеем:

z dxdydz Rcos R2 sin dRd d

V					V*				1
1			4				2	R4	1	1
								R4		1	2 cos2
R3dR sin cos d d												0	4
R3dR sin cos d d								4		4		0	4
0			0				0	4	0	4

		cos			cos0		.
	8	cos		2	cos0	8	.
	8			2		8

Приложения тройного интеграла

Тройные интегралы позволяют:

1. Вычислить объемы и массу пространственных тел.

Взадаче №3 лекции №9 масса пространственной области V

сизвестной функцией распределения плотности x, y,z

определяется по формуле

M x, y,z dxdydz.

(10)

Формула (10) выражает физический смысл тройного интеграла. Если в формуле (10) положить x, y,z 1, то получим формулу для вычисления объема пространственной области V :

V dxdydz.

(11)

Перейдя к цилиндрическим и сферическим координатам, получим соответственно:

V d d dz

– объем в цилиндрических координатах,

V R2 sin dRd d

–в сферических координатах.

2.Центры тяжести и моменты инерции пространственных

тел.

Имеют место формулы:

		x x, y,z dxdydz
		V
xc		V	;
xc		x, y,z dxdydz	;
		x, y,z dxdydz
		V
		y x, y,z dxdydz
		V
y		V	;
y	c	x, y,z dxdydz	;
	c	x, y,z dxdydz

z x, y,z dxdydz

	V
zc	V	.
zc	x, y,z dxdydz	.
	x, y,z dxdydz
	V

(12)

			y2 x, y,z dxdydz;
JOx x2			y2 x, y,z dxdydz;
	V
	V
	x2		z2 x, y,z dxdydz;
JOy	x2		z2 x, y,z dxdydz;
	V
	y	2	x	2	x, y,z dxdydz.
JOz	y		x		x, y,z dxdydz.

(13)

Пример.

Найти центр тяжести однородного многогранника

( x, y,z const), ограниченного плоскостями x 1;	y 1;	z 0;
y z 2 0 (рис. 8).

							2
																		y
																		y

															1

										C		1			4			7
															;		;
															;		;
				1								2			9			9
		x		1
		x
						Рис. 8
						0 x 1;
							0 y 1;
					V		0 y 1;
							0 z 2 y.
							0 z 2 y.
				dxdydz VD1														3			.

																				2
					V																									y2 1
		1		1		2 y	1					1												1						y2 1						3
xdxdydz xdx dy dz												2 y dy													2y														;
xdxdydz xdx dy dz												2 y dy													2y											4			;
V		0		0	0		2					0									2							2						0		4
		1		1		2 y					1		1																	y3 1						2
ydxdydz dx ydy dz													y 2 y dy y2																									;
ydxdydz dx ydy dz											2		y 2 y dy y2																							3		;
V		0		0	0						2		0															3					0			3
		1		1	2 y		1				1			2 y 2												2 y 3 1										7
zdxdydz dx dy zdz																					dy																		;
zdxdydz dx dy zdz															2						dy							6								6			;
V		0		0	0		2				0				2													6							0	6
xc	3 4		1	; yc		2 3		4	; zc							7 6						7	; C				1	;	4		;	7			.
xc				; yc					; zc														; C					;			;				.
3 2 2					3 2 9										3 2 9										2 9 9
Лекция № 13. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Зададим		в		пространстве									кусок								гладкой								поверхности
F x, y,z 0							и																		вектор-функцию
a P x, y,z i Q x, y,z j R x, y,z k ,																			определенную																во		всех
точках куска поверхности (рис. 1).

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 189 10 11 12 13 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021356.7 Кб2221.pdf
#
07.01.20214.09 Mб22210.pdf
#
07.01.20214.09 Mб122211.pdf
#
07.01.20214.09 Mб62212.pdf
#
07.01.20214.16 Mб52215.pdf
#
07.01.20214.17 Mб12216.pdf
#
07.01.20214.17 Mб62217.pdf
#
07.01.20214.17 Mб52218.pdf
#
07.01.20214.19 Mб192219.pdf
#
07.01.2021357.51 Кб1222.pdf
#
07.01.20214.2 Mб02220.pdf