
2216
.pdf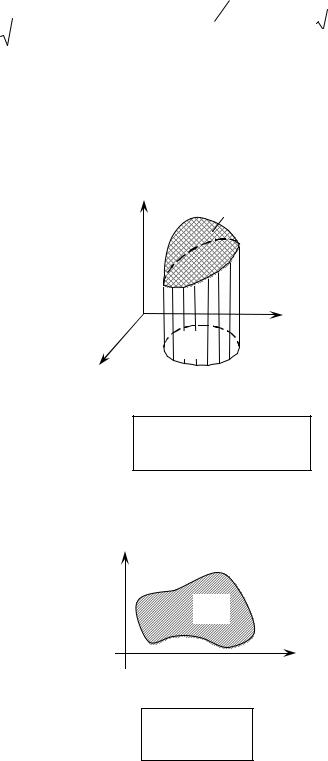
2 |
1 |
|
|
|
|
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
d |
|
|
|
|
1 2 |
2 |
|
|
2 2 2 1 |
|
||||
1 |
2 |
d 2 |
|
3,83. |
||||||||||
|
|
3 |
|
|
3 |
|
|
|||||||
0 |
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Лекция № 11. ПРИЛОЖЕНИЯ ДВОЙНОГО ИНТЕГРАЛА
1. Вычисление объемов и площадей.
Решение этих задач основано на геометрическом смысле двойного интеграла (рис. 1).
z |
z f x, y |
0
y
x D
Рис. 1
Vц.т f x, y dxdy.
D
(1)
Если положить f x, y 1, получим цилиндр высотой, равной 1, а его объем численно равен площади области D (рис. 2).
y
D
0 x
Рис. 2
SD dxdy .
D
(2)
Если в формуле (2) перейти к полярным координатам (рис. 3), получим формулу для вычисления площади в полярных координатах:

y |
2 |
D
|
1 |
0 |
x |
Рис. 3 |
|
SD d d .
D*
(3)
;
D*:
1 2 .
2
SD dx d .
1
Примеры.
1. Вычислить объем тела, ограниченного цилиндром
x2 y2 |
1, плоскостью z 0, |
x y z 3(рис. 4, а), б)). |
||||||
|
а) |
|
|
|
z |
б) |
y |
D |
|
|
|
|
1 |
||||
|
|
|
|
|
z 3 x y |
|
x |
|
|
|
|
|
|
0 |
1 |
||
|
|
|
|
|
|
1 |
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
в) |
z |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
3 |
|
y |
|
|
|
|
|
|
||||
|
|
|
|
|
|
y |
|
|
|
x |
3 |
|
|
D |
0 |
x |
|
|
|
|
|
|||||
|
|
|
|
Рис. 4 |
|
|||
|
|
|
|
|
|
|
|
|
0 2 ;
D*:
0 1.
V 3 x y dxdy 3 sin cos d d
D |
D* |
2 1
d 3 2 sin 2 cos d 3 .
0 0

2. Найти площадь фигуры, ограниченной линиями y sin x; y cos x; x 0 (рис. 5).
y |
D |
|
|
sin x |
||
|
|
|
||||
0 |
|
|
|
|
|
x |
|
4 |
|
|
cosx |
||
|
|
|
Рис. 5 |
|||
|
|
|
|
|||
|
|
|
|
; |
||
|
4 |
|||||
D*: 0 x |
||||||
|
|
|
|
|
||
|
sin x y cosx. |
|||||
4 cos x |
4 |
|
|
|
||
SD dxdy dx dy cosx sin x dx 
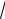 2 1 0,41.
2 1 0,41.
D |
0 sin x |
0 |
2. Площадь поверхности.
Рассмотрим кусок простой (две разные точки поверхности не должны проецироваться в одну точку плоскости z 0) поверхности z f x, y , ограниченный замкнутой кривой. Спроецировав его на плоскость z 0, имеем плоскую область D0
(рис.6).
z |
z f x, y |
i
 Mi
Mi
0 |
|
y |
|
|
Pi |
|
|
x |
|
|
|
|
D |
|
|
|
Рис. 6 |
|
|
Разобьем область D на |
n участков |
с площадями |
Si и |
диаметром di , d maxdi и |
выберем на |
любом участке |
точку |
Pi xi, yi . Этой процедуре будет соответствовать разбиение куска поверхности на участки с площадями i и фиксированными точками Mi xi, yi,zi , т.е. ПрOxy i Si ; ПрOxyMi Pi .

n
Очевидно, что площадь куска поверхности i . За
i 1
приближенное значение i возьмем площадь куска касательной
плоскости |
в |
точке |
Mi |
к |
поверхности |
z f x, y , |
проецирующегося в Si |
области D0. |
|
|
|||
Пусть i |
– касательная плоскость к поверхности в точке Mi . |
|||||
Ni i – нормальный вектор (рис. 7).
|
|
F |
|
|
F |
|
|
|
F |
|
|
|
Ni |
|
|
M |
; |
|
M |
i |
; |
|
M |
i |
|
|
|
|
||||||||||
|
|
x |
i |
|
y |
|
|
z |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
z |
|
|
|
|
|
Ni |
|
|
|
|
|
|
|
|
|
|
|
|
Mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
Ni |
|
k |
j |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
i |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
Pi |
Si |
||
x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7
для поверхности z f x, y f x, y z 0 или F 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
F |
M |
|
|
f |
P ; |
F |
M |
|
|
|
f |
|
P ; |
F |
M |
1. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x |
|
i |
|
|
|
x |
i |
|
y |
|
i |
|
|
|
y |
i |
|
|
|
z |
|
i |
|
||||||||||||
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Ni |
|
|
|
|
|
P |
; |
|
|
P |
;1 , k |
0;0;1 . |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
i |
|
|
|
y |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ni k |
|
|
|
|
|
|
|
|
|||||||
Пусть i |
i |
xoy Ni |
k cos i |
|
|
|
|
|
; |
|
|
|
|
|||||||||||||||||||||||
|
Ni |
|
k |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
cos i |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
f |
|
|
2 |
f |
|
|
|
|
2 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
P |
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
y |
i |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пусть ПрOxy i* Si Si |
i *cos i ; |
|
|
|
|
||||||||||||
|
|
S |
i |
|
|
f |
|
|
2 |
f |
|
|
2 |
|
|
||
|
* |
|
|
1 |
|
|
P |
|
|
|
P |
|
|
S |
. |
||
|
|
|
|
||||||||||||||
i |
|
cos i |
|
x |
|
i |
|
y |
i |
|
|
i |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Итак, имеем приближенное значение площади к поверхности:
|
n |
|
|
|
n |
|
f |
2 |
|
f |
|
2 |
|
|
||
|
|
|
i |
* |
|
1 |
|
|
P |
|
|
|
P |
S |
i |
. |
|
|
|||||||||||||||
|
|
|
|
x |
i |
|
y |
i |
|
|
||||||
|
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
||
Переходя к пределу, имеем формулы для вычисления площади поверхности (рис.8).
|
n |
|
f |
|
|
2 |
|
f |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
1 |
P |
|
|
|
P |
|
S |
|
|
|||||
|
|
|
i |
||||||||||||
n |
|
x |
i |
|
|
|
|
|
i |
|
|
|
|||
i 1 |
|
|
|
|
|
|
y |
|
|
|
|
|
|||
d 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
D
|
f |
2 |
|
f |
|
2 |
1 |
|
|
|
|
|
dxdy. |
|
|
|||||
|
|
|
|
|
|
|
|
x |
|
y |
|
||
z
0y
xD
Рис. 8
|
|
|
|
|
|
|
|
|
|
|
|
f 2 |
f 2 |
dxdy |
|
||||
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
. |
||
|
D |
x |
y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
(4)
Пример.
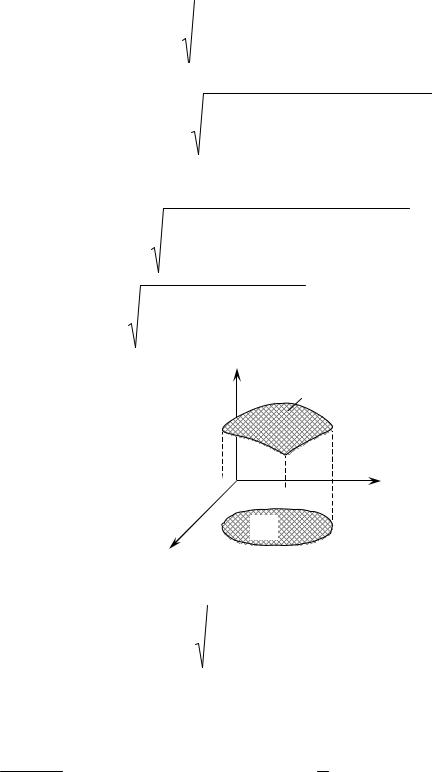
Вычислить площадь поверхности параболоида вращения z x2 y2 , отсекаемой плоскостью z 1 (рис. 9).
2 |
2 |

|
x2 y2 |
|
|
|
|
|
|
|
|||
z |
|
|
|
|
; |
|
|
|
|
|
|
|
2 |
|
1 |
– |
уравнение |
окружности, |
|||||
|
|
x2 y2 |
|||||||||
z |
1 |
; |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
ограничивающей область D. |
|
|
|
|
|||||||
а) |
|
|
|
z |
1 |
|
|
б) |
y |
|
|
|
|
|
z |
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
1 |
D |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
1 |
0 |
1 x |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y |
|
|
1 |
||
|
|
|
|
|
|
|
|
||||
|
|
|
x |
D |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Рис. 9
Находим площадь по формуле (4): так как z x2 y2 , отсюда
2
z |
x; |
z |
y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
1 x2 y2 |
|
dxdy d |
1 2 |
d |
|||||||||||||
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
2 2 |
1 2 3 2 |
|
1 |
|
2 |
2 3 2 |
1 |
2 2 |
|
|
1 3,83. |
||||||||
|
|
|
|
|
2 |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
2 3 |
|
|
0 |
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3. Центр тяжести плоской фигуры.
Определение. Статическим моментом материальной точки относительно оси называется произведение массы этой точки на её расстояние до оси.
Статический момент системы материальной точки определяется суммарно (рис. 10).
Определение. Центр тяжести – это такая точка, статический момент которой, при условии, что в ней сосредоточена вся масса системы, равен суммарному моменту.

y |
|
A1 |
A xc , yc |
||||
|
|
|
|
|
|||
|
|
A |
|
|
A2 |
||
|
|
3 |
|
|
|||
0 |
|
Рис. 10 |
|
x |
|||
|
|
|
|
||||
Откуда |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
ximi |
|
|
|
x |
c |
|
|
|
i 1 |
; |
|
|
|
n |
|||||
|
|
|
|
|
|
||
|
|
|
|
|
mi |
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
yimi |
|
|
|
|
|
|
|
|
|
||
yc |
|
i 1 |
|
. |
|||
n |
|
||||||
|
|
|
|
|
mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
(5)
Зададим плоскую область D с распределением плотности
x, y .
y
|
Pi |
|
Si |
0 |
x |
|
Рис. 11 |
Разобьем область D на |
n участков с площадями Si и |
диаметрами di , d maxdi , выберем на любом участке точку Pi xi, yi . Считая, что масса каждого участка сосредоточена в
выбранной точке Pi xi, yi и равна mi Pi Si , приходим к системе материальных точек (рис.11). В силу формул (5) находим приближенное значение координат центра тяжести:
n
xi xi, yi Si
x |
c |
|
i 1 |
; |
|
n |
|||||
|
|
|
xi, yi Si
i 1 n
yi xi, yi Si
y |
c |
|
i 1 |
. |
|
n |
|||||
|
|
|
xi, yi Si
i 1
Переходя к пределу при n и d 0, имеем формулы для вычисления центра тяжести:
|
|
x x, y dxdy |
|
|
|
|
|
||
xc |
|
D |
; |
|
x, y dxdy |
||||
|
|
|
||
|
|
D |
|
|
|
|
|
y x, y dxdy
|
|
D |
|
|
yc |
|
|
. |
|
x, y dxdy |
||||
|
|
|
D
(6)
Пример.
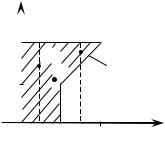
Найти центр тяжести однородного профиля (рис.12).
y
M |
2 |
2 |
|
M1 |
y x |
C |
|
1 |
|
0 1 2 x
Рис. 12
D D1 D2.
0 x 1;
D1
0 y 2;
1 x 2;
D2
x y 2.
Так как профиль однородный, то x, y 1.

Тогда
|
|
|
xdxdy |
|
|
|
|
|
|
|
ydxdy |
|
|
|
|
|
|
|
|
|
|
|||||||
x |
c |
|
D |
|
|
; y |
c |
|
|
|
D |
|
; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
dxdy |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
D |
|
|
|
5 |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dxdy SD |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
D |
|
|
|
1 |
|
|
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|||||||||
|
xdxdy xdx dy xdx dy |
|
. |
|
||||||||||||||||||||||||
|
|
3 |
||||||||||||||||||||||||||
|
|
D |
|
|
|
0 |
|
|
|
|
0 |
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
2 |
|
|
|
2 |
2 |
|
|
|
|
|
17 |
|
|||||||||
|
ydxdy dx ydy dx ydy |
. |
||||||||||||||||||||||||||
|
|
6 |
||||||||||||||||||||||||||
|
|
D |
|
|
|
0 |
0 |
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
xc |
2 |
|
yc |
17 6 |
|
|
17 |
C |
|
2 |
|
|
2 |
|||||||||||||
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
;1 |
|
|
|
|
|
. |
||||||
|
|
|
5 2 |
|
|
15 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 15 |
|||||||||||||||
4. Момент инерции плоской фигуры.
Определение. Моментом инерции материальной точки относительно оси называется произведение массы этой точки на квадрат расстояния до оси. Момент инерции системы материальных точек определяется суммарно.
y |
Si |
|
|
|
Pi |
0 |
x |
|
Рис. 13 |
Пусть задана плоская область D с функцией распределения плотности x, y . Разбиваем на n участков с площадями Si и диаметрами di , выбирая на каждом участке точку Pi xi, yi (рис.13). Считая, что в выбранной точке Pi xi, yi сосредоточена вся масса участка mi Pi Si , имеем:
n
JOx yi2 xi, yi Si ; i 1
n
JOy xi2 xi, yi Si . i 1
Переходя к пределу при n и d 0, имеем формулы для вычисления моментов инерции относительно осей:

JOx y2 |
x, y dxdy; |
||
|
D |
|
|
|
x, y dxdy. |
||
x2 |
|||
JOy |
|||
D
(7)
Соответственно момент инерции относительно центра О определится, как
J0 x2 y2 x, y dxdy.
D
(8)
5. Решение задач механики.
Для решения задачи №2 лекции №9 (рис.14) получим формулу для вычисления объема жидкости через поперечное сечение трубы (секундный расход)
V x, y dxdy.
D
(9)
y
x, y
D
0 x
Рис. 14
x, y пл.D.
Лекция № 12. ТРОЙНОЙ ИНТЕГРАЛ, ВЫЧИСЛЕНИЕ И ПРИЛОЖЕНИЯ
Пусть задана пространственная замкнутая и ограниченная область U и функция 3-х переменных u f x, y,z , определенная в любых точках области V (рис. 1).
z
|
0 |
x |
y |
i |
|
|
Pi |
|
Рис.1 |
