
2216
.pdf
т.к. V V2 V2 20.
30. Т е о р е м а о среднем:
f x, y dxdy f , SD ,
D
где существует точка , D. То есть объем цилиндрического тела равен объему цилиндра с площадью основания SD и высотой
f , .
Повторные интегралы по правильным областям и их свойства
Определение. Плоская область D называется правильной в направлении оси Oy, если она ограничена прямыми x a x b и кривыми y 1 x и y 2 x (рис. 7).
Координаты любой точки области D удовлетворяют неравенствам:
a x b; |
|
|
|
|
|
|
||
|
|
x y |
|
x . |
|
|||
|
2 |
|
||||||
|
1 |
|
|
|
|
|
|
|
y |
|
|
y 2 x |
|
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
||
|
|
|
y 1 |
x |
x |
|||
|
|
|
|
|
|
|
|
|
0 |
|
a |
x |
|
|
b |
|
|
Рис. 7
Определение. Повторным интегралом по правильной в направлении оси Oy области D от функции f x, y называется
число, полученное следующим двукратным интегрированием:
|
b 2 |
x |
|
|
|
JD |
|
f |
x, y dy |
|
|
|
dx, |
||||
|
|
1 |
x |
|
|
|
a |
|
|
||
при интегрировании в скобках x считается const.
Пример.
Вычислить повторный интеграл по области (рис. 8)

|
|
|
|
|
|
|
|
|
|
|
|
|
0 x 1; |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 1. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
y 1 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
x |
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8 |
|
|
|
|
|
|
|
|
|
||||
|
1 1 |
|
|
2 |
|
|
1 |
|
|
|
|
y |
3 |
1 |
1 |
|
1 3 |
x |
6 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
JD x y dy dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
xy |
|
|
|
|
|
|
x |
|
|
|||||||||||||||||
3 |
dx x |
3 |
3 |
dx |
||||||||||||||||||||||
|
0 x2 |
|
|
|
|
|
0 |
|
|
|
|
x2 |
0 |
|
|
|
||||||||||
x2 |
x |
x4 |
|
x7 1 |
15 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
21 0 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Определение. Область D называется правильной в |
||||||||||||||||||||||||||
направлении оси Ox, если она ограничена прямыми y c, |
y d и |
|||||||||||||||||||||||||
кривыми x 1 y , x 2 y (рис. 9).
Координаты любой точки области D удовлетворяющие неравенствам:
c y d;
1 y x 2 y .
y
x 1 y
d 
x 2 y
M y 

c
D
0 |
x |
Рис. 9

Определение. Повторным интегралом по правильной в
направлении оси Ox области |
D от функции f x, y называется |
||||
число |
d 2 y |
|
|
||
|
|
|
|||
JD |
|
|
f |
x, y dx |
|
|
|
dy, |
|||
|
|
1 y |
|
|
|
|
c |
|
|
||
при интегрировании в скобках y считается const.
Пример.
Вычислить повторный интеграл по области (рис. 10)
|
|
|
|
|
|
|
|
|
|
|
|
0 y 1; |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
0 x |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
y 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y x2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
1 |
|
|
y |
|
|
|
|
|
|
1 |
|
x2 |
|
|
|
|
|
1 |
y |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
JD dy x y |
2 |
|
|
|
|
|
|
|
|
|
|
y |
2 |
x |
|
|
|
|
y |
5 2 |
dy |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
dx dy |
|
|
|
|
|
2 |
|
||||||||||||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|||||||
y2 |
2 |
|
y |
7 2 |
1 |
1 2 15 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
7 |
|
|
|
0 |
4 |
7 |
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
З а м е ч а н и е. Области, правильные в обоих направлениях, называются просто правильными (рис. 11).
y
d 
c |
|
|
|
0 |
а |
b |
x |
|
|
Рис. 11 |
|

a x b; |
|
|
и |
c y d; |
|
|
|
||||||
|
|
x y |
|
x |
|
1 y |
|
|
|
|
y . |
||
|
1 |
2 |
|
|
x |
2 |
|||||||
|
|
|
|
|
|
|
|
||||||
По правильной |
области |
от |
|
f x, y |
|
можно составить 2 |
|||||||
повторных интеграла: |
|
|
|
2 x |
|
|
|
|
|
|
|||
|
|
|
|
b |
|
|
|
|
|
|
|
||
|
|
|
JD dx f x, y dy; |
|
|
|
|||||||
|
|
|
|
a |
|
1 x |
|
|
|
|
|
|
|
|
|
|
|
d |
|
2 y |
|
|
|
|
|
|
|
|
|
|
JD* dy |
f x, y dx. |
|
|
|
||||||
c 1 y
Геометрически правильные области обладают тем свойством, что прямые параллельны Ox и Oy, пересекают границу области не более чем в двух точках (рис. 12, а), б)).
а) y |
Неправильная |
б) |
y |
Неправильная |
|
в направлении y |
|
|
|
D
D
0 |
x |
0 |
x |
Рис. 12
Свойства повторных интегралов
10 . Геометрический смысл повторного интеграла. Повторный интеграл по правильной в каком-либо
направлении области D от функции f x, y равен объему цилиндра, ограниченного снизу областью D, сверху поверхностью z f x, y , а по бокам прямыми, параллельными оси Oz (рис. 13).
Д о к а з а т е л ь с т в о Пусть область D правильная в направлении Oy.
a x b; |
|
|
||
|
|
x y |
|
x . |
|
1 |
2 |
||
|
|
|
||
Построим цилиндрическое тело, указанное в определении свойства 10 , и возьмем x a,b .

z
0
Рассмотрим
z f x, y |
|
z f x, y |
|
|
|
|
|
|
S x |
|
|
y |
|
|
|
y2 |
|
|
y 2 x |
|
|
|
|
y1 |
|
|
y x |
|
|
|
1 |
a |
x |
b |
x |
|
Рис. 13 |
|
|
b |
2 x |
|
|
JD dx f x, y dy.
|
|
a |
1 x |
|
|
2 |
x |
y2 |
|
y1 1 x ; y2 2 x . |
f x, y dy f x, y dy Sкр.тр. |
S x – |
||
|
1 |
x |
y1 |
|
площадь поперечного сечения цилиндрического тела.
b
JD S x dx Vц.т .
a
20. Повторные интегралы по правильным областям не зависит от порядка интегрирования, т.е. JD JD* .
b 2 x d 2 y
dx f x, y dy dy f x, y dx.
a 1 x c 1 y
Лекция № 10. СВЕДЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
КПОВТОРНЫМ. ЗАМЕНА ПЕРЕМЕННЫХ
ВДВОЙНОМ ИНТЕГРАЛЕ
Вычисление двойных интегралов ведется на основании теоремы.
Т е о р е м а. Двойной интеграл по правильной области D от
функции |
f x, y равен повторному интегралу по этой области от |
|||
этой же функции, т.е. |
2 x |
|
2 y |
|
|
b |
d |
||
f x, y dxdy dx f x, y dy dy |
f x, y dx. |
|||
D |
a |
1 x |
c |
1 y |
Д о к а з а т е л ь с т в о Следует из геометрического смысла двойного и повторного
интегралов.
Пример.
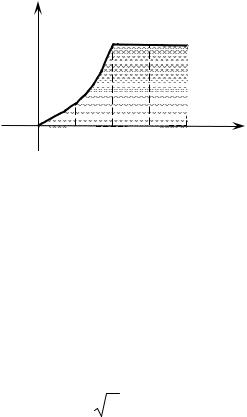
Вычислить xydxdy по области (рис. 1)
D
Первый способ: представим область D, в виде
0 x 1; D: 0 y x2;
D1
1 x 2;
0 y 1;
D2
y
y 1
D
|
|
|
|
|
0 |
|
x |
|
1 |
|
x 2 |
|
x |
|
|||
|
|
|
|
|
|
|
|
|
|
|
Рис. 1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x2 |
2 |
1 |
|
xydxdy |
, |
|
т.е. xydxdy xdy ydx xdy ydx |
||||||||||||||
D |
|
D1 |
D2 |
|
|
|
D |
|
|
|
|
0 |
0 |
1 |
0 |
||
1 |
x5 |
1 |
2 |
1 |
|
3 |
|
10 |
|
5 |
|
|
|
|
|||
|
|
dx |
|
xdx |
|
|
|
|
|
|
|
|
|
. |
|
|
|
2 |
2 |
12 |
4 |
12 |
6 |
|
|
|
|||||||||
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Второй способ: представим область D, как единую (рис.2)
0 y 1;
D:
y x 2.
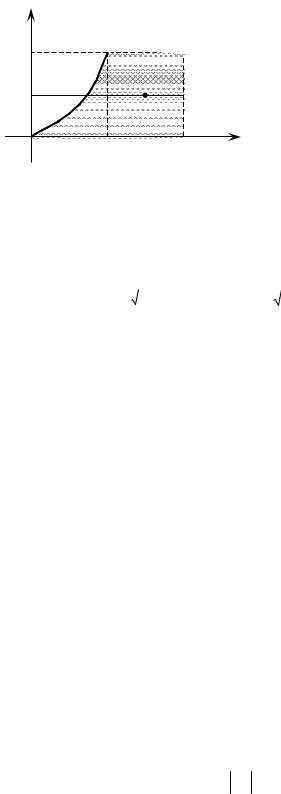
y
y x2
1
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
1 |
|
x2 |
2 |
|
|
||||
xydxdy ydy |
xdx y |
|
|
|
|
|
|
dx |
||||||||||||||||||
2 |
|
|||||||||||||||||||||||||
D |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
y |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
|||||||||||||||
1 |
|
|
|
|
|
y |
|
|
|
|
|
|
y3 |
1 |
|
5 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y |
2 |
|
dy y2 |
|
|
|
|
|
. |
|
|
|
|
|||||||||||||
2 |
6 |
|
|
|
|
|
||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
6 |
|
|
|
|
|
||||||
Зададим f x, y dxdy и сделаем замену его переменных по
D
формуле
x u,v ;
y u,v .
(1)
Составим по формуле (1) определитель 2-го порядка, который называется Якобианом замены переменных:
|
|
x |
|
|
|
x |
|
||
|
|
u |
|
|
|
v |
|
. |
|
|
|
y |
|
|
|
y |
|
||
|
|
u |
|
|
|
v |
|
|
|
(2)
Т е о р е м а. Если 0 в области D, то имеет место формула
f x, y dxdy f u,v , u,v dudv.
D |
D* |
(3) |
|
Пример. |
|
Вычислить x y 3 x y 2 dxdy по области ABCD (рис.3).
D
y
D
2 
1 C
0 |
1 |
2 |
x |
Рис. 3
x y 1; |
AB |
|
CD |
x y 3; |
|
|
AD |
x y 1; |
|
|
BC |
x y 1; |
0 x 1;
1 x y x 1;
D1
1 x 2;
x 1 y 3 x.
D2
Сделаем замену переменных, положив:
x y u; |
x |
1 |
|
u v ; |
|
1 |
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
2 |
2 |
|
|
|
1 |
. |
|||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||||
x y v; |
y |
1 |
u v ; |
|
|
1 |
|
|
1 |
|
2 |
|
||||
2 |
|
2 |
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||
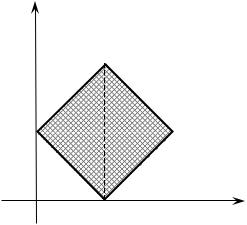
В результате замены, получим область D* (рис.4) |
||||||||||||||||
|
u 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 u 3; |
|
|
|
|
|
|
|
|
|||
|
u 3; |
|
|
|
|
|
|
|
|
|||||||
|
D*: |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
v 1; |
1 v 1. |
|
|
|
|
|
|
|
|
||||||
v 1;

y |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
3 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
Рис. 4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
x y 3 |
x y 2 |
dxdy u3v2 |
|
|
1 |
|
dudx |
||
|
|
||||||||
|
2 |
|
|||||||
D |
|
|
D* |
|
|
|
|
|
|
31
1 u3du v2dv 20.
32
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Двойной интеграл в полярных координатах (рис. 5). |
|
|||||||||||||||||||
|
y |
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Рис. 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
def |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M OM xi yi M x, y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
M x, y – декартовы координаты точки |
M ; |
|
OM |
|
|
– |
||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M , |
|
|||||
полярный радиус; OM OX |
|
|
– |
полярный |
угол; |
|
– |
|||||||||||||
полярные координаты точки M . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
0; 0 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Формулы перехода: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x cos ; |
|
|
|
|
|
x |
2 |
y |
2 |
; |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|||
y sin ; |
|
|
|
tg |
|
|
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
(4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В f x, y dxdy сделаем замену переменных по формуле (4):
|
D |
|
|
x |
|
x |
|
|
|
|
|
|
|
|
|
x cos ; |
|
|
|
|
|
sin |
cos |
|
|
|
|||||
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
||||||||||||
|
|
|
|
y |
|
y |
|
|
|
|
|
||||
y sin ; |
|
|
|
|
|
cos |
sin |
|
|
|
|||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
||||||||||||
|
|
xydxdy f cos , sin d d |
, |
||||||||||||
|
|
D |
|
|
D* |
|
|
|
|
|
|
|
|
|
|
|
|
(5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
где D* – область D в полярных координатах.
Формула (5) называется формулой перехода к полярным
координатам. |
|
|
|
|
|
|
|
|
|
Пример. |
|
|
|
|
|
|
|
|
|
Вычислить |
|
x2 y2 |
|
||||||
1 x2 y2 |
dxdy по области D: |
1. |
|||||||
|
|
|
D |
|
|
|
|
|
|
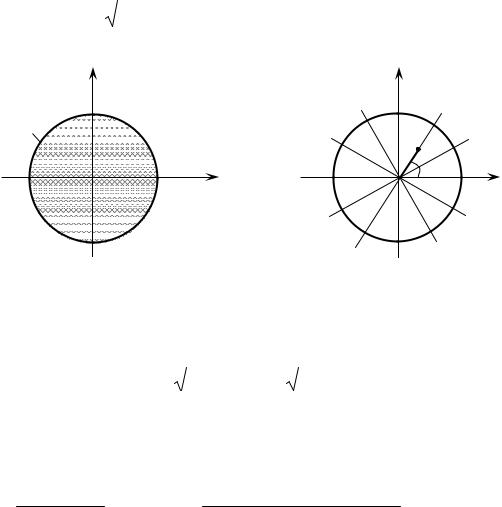
а) |
y |
|
|
б) |
y |
|
|
||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
x |
|
0 |
x |
||
|
|
|
|
|
|
|
|
|
|
Рис. 6
Область D рассмотрим в виде (рис. 6, а))
D: |
1 x 1; |
||||
|
|
|
|
|
|
|
|
||||
|
1 x2 y 1 x2 . |
||||
Перейдем к полярным координатам (рис 6, б))
0 2 ;
0 1.
Воспользуемся формулой (5):
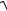
 1 x2 y2 dxdy
1 x2 y2 dxdy 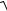
 1 2 cos2 2 sin2 d d
1 2 cos2 2 sin2 d d
D |
D* |
