2216

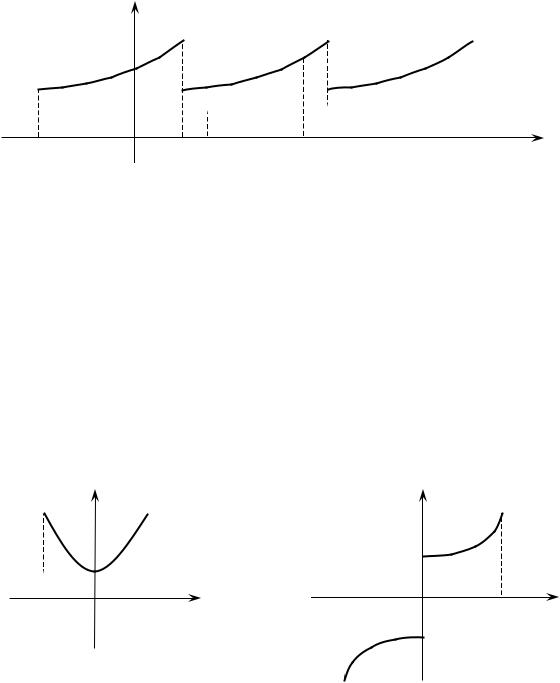
y

f x f1 x

0 a b 2 4 x

Рис. 7

Разложим f1 x в ряд Фурье. Сумма этого ряда во всех точках отрезка a, b (кроме точек разрыва) совпадает с заданной функцией f x , т.е. мы разложим функцию f x в ряд Фурье на отрезке a, b .

Рассмотрим следующий важный случай. Пусть функция f x задана на отрезке 0, . Дополняя определение этой функции произвольным образом (четное или нечетное продолжение) на отрезке , 0 , раскладываем её в ряд Фурье (рис. 8, а), б)).

Рис. 8

Примеры.

1. f x x на отрезке 0, в ряд Фурье по синусам (рис. 9). Решение. Продолжая эту функцию нечетным образом, получим ряд

y

y

Рис. 10

Лекция № 25. ПРИБЛИЖЕНИЕ В СРЕДНЕМ ЗАДАННОЙ ФУНКЦИИ С ПОМОЩЬЮ ТРИГОНОМЕТРИЧЕСКОГО МНОГОЧЛЕНА

Представление функции бесконечным рядом (Фурье, Тейлора и т.д.) имеет на практики тот смысл, что конечная сумма, получающаяся при обрывании ряда на n-ом члене, является

приближенным выражением разлагаемой функции; это приближенное выражение можно довести до какой угодно степени

Вернемся теперь к нашей задаче. Пусть дана периодическая с периодом 2 функция f x . Среди всех тригонометрических многочленов n-го порядка:

Требуется найти путем выбора коэффициентов k и k тот многочлен, для которого среднее квадратичное уклонение,

определяемое равенством

имеет наименьшее значение.

Задача сводится к нахождению минимума функции 2n 1 переменных 0, 1, , n, 1, , n. В результате получим, что среди всех тригонометрических многочленов порядка n наименьшее среднее квадратичное уклонение от функции f x имеет тот многочлен, коэффициенты которого являются коэффициентами Фурье функции f x .

Величина наименьшего квадратичного уклонения равна

(1)

Это соотношение называется неравенством Бесселя. Отметим без доказательства, что n2 0 при n . Тогда из

формулы (1) вытекает равенство

которое называется равенством Ляпунова-Парсеваля.

Это равенство доказано для значительно более широкого класса функции, чем тот, который мы рассматриваем (т.е. кусочномонотонных функций). Таким образом, для функции, удовлетворяющей равенству Ляпунова-Парсеваля, соответствующий ряд Фурье дает среднее квадратичное уклонение, равное нулю.

Отметим без доказательства также следующее свойства коэффициентов Фурье для кусочно непрерывной на отрезке a, b функции f x .

результате получим тождество

Практический гармонический анализ

Теория разложения функций в ряды Фурье называется

гармоническим анализом.

Сделаем несколько замечаний о приближенном вычислении коэффициентов ряда Фурье, т.е. о практическом гармоническом анализе.

Как известно, коэффициенты Фурье для функции f x , имеющей период 2 , определяются по формулам:

задается или в виде таблицы (когда функциональная зависимость получается в результате эксперимента), или в виде кривой, которая вычерчивается каким-либо прибором. В этих случаях коэффициенты Фурье вычисляются при помощи приближенных методов интегрирования.

Будем рассматривать промежуток x длины 2 . Этого можно добиться соответствующим выбором масштаба по

соответственно через y0, y1, , yn .

Эти значения мы определяем или по таблице, или по графику данной функции измерением соответствующих ординат. Тогда, пользуясь, например, формулой прямоугольников, определяем коэффициенты Фурье:

Разработаны схемы, упрощающие вычисление коэффициентов Фурье (см. литературу). Существуют приборы (гармонические

анализаторы), которые по графику данной функции позволяют вычислить приближенные значения коэффициентов Фурье.

Интеграл Фурье

Пусть функция f x определена на бесконечном интервале, и абсолютно интегрируема на нем, т.е. существует интеграл

Стоящее справа выражение называется интегралом Фурье для функции f x .

Преобразуя интеграл, стоящий в правой части равенства (6), раскрыв cos t x , имеем:

cos t x cos tcos x sin tsin x.

(7)

Подставляя (7) в формулу (6) и вынося cos x и sin x за знаки интегралов, где интегрирование совершается по переменной t, получим