Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2191.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

3.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 207 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

6. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ

6.1. Рекомендации для проведения практического занятия

Цель практического занятия: отработка навыков решения задач на составлен е уравнен й движения точки в параметрической форме и определен е к немат ческих характеристик движения точки.

Перед	зучен ем данной темы рекомендуется повторить со
понятиекр в зны рад уса кривизны кривой.
студентами следующ е вопросы из курса математики: проецирование
Свекторов на ось, плоскость; правила дифференцирования векторных
функц й скалярного аргумента; дифференцирование сложных функций.
Необход мо также		повторить перед	занятием следующие вопросы из
	б
раздела «К немат ка»: спосо ы задания движения точки, основная задача
кинемат ки	точки,	к нематические	характеристики движения точки,

Требован я к знан ям студента:

1.		А
	Уметь прав льно формулировать теоремы кинематики.
2.	Знать алгоритмы определения величины и направления скоростей и
ускорений точки.
3.	Уметь производить кинематический расчет простых механизмов.

6.2. Методические рекомендации к решению задач

Задачи по кинематике точки могут предполагать:

1.Составление кинематических уравнений движения точки.

2.Определение по заданным кинематическим уравнениям движения точки ее траектории, положения точки, скорости, ускорения и радиуса кривизны траектории.

3.Переход от уравнений движения точки в декартовых координатах к полярным или к естественному способу задания движения.

4.Определение по некоторым заданным кинематическим параметрам движения точки других ее параметров.

Задачи решаются в такой последовательности:

1.Выбирается неподвижная система координат – декартовая, полярная или какая-либо иная; начало координат и та или иная системаДИ

координат выбираются исходя из условий задачи так, чтобы решение задачи было возможно более простым.

2. Составляются кинематические уравнения движения точки, если они не заданы.

3. По известным соотношениям кинематики находятся все величины, требуемые по условию задачи.

4. Изображаются траектория движения, векторы скорости и ускорения точки.

Методика задач четвертого типа существенно зависит от исходных
условий. В ряде случаев, когда уравнения движения точки не заданы и в
С
качестве исходных данных приводятся скорости или ускорения точки,
необходимые для ответа на поставленные вопросы соотношения находят
путем	нтегр рован я дифференциальных	зависимостей между
кинемат ческ ми вел ч нами. Появляющиеся		при этом постоянные
интегр
	рован я определяют по начальным условиям.

6.3. Контрольные вопросы для тестирования студентов

	способ
1. Как е существуют спосо ы задания движения точки?
Способы задан я движения точки: векторный, координатный,
естественный.
2. Оп ш те векторный					задания движения точки.
При векторном спосо е задания движения положение точки на
траектории определяют концом радиуса-вектора r , проведенного из
некоторой неподвижной точки О:
					r = r( t ).
Векторное уравнение представляет собой уравнение движения точки.
					Д
Точка движется по траектории, которая задана концом радиуса-вектора.
Уравнение можно записатьАв проекциях на декартовы оси координат Ox,
Oy, Oz в виде				r = i х + jy + kz,

где i , j ,k –	единичные векторы-орты координатных осей.
3. Опишите естественный способ задания движения точки.
При естественном				способе	задания	И
движения точки задают: траекторию
точки; начало и направление отсчёта
дуговой	координаты			s,	которая
отсчитывается		от	начала		отсчета.
Известно, что элемент дуги ds связан с
координатами		движущейся			точки
следующим уравнением:

ds = 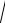(dx)2 + (dy)2 + (dz)2 .

Интегрируя это уравнение, получим уравнение движения точки

								s(t) = ∫t		Vdt .
									0
4.	Опишите			координатный					способ
задания движения точки.
Движение				точки			задают			в
декартовой системе					координат				путем
задания	коорд		нат		точки			в	виде
скалярных функц й времени
х=f1(t); у= f2(t);							z= f3(t).
С
5. Как определя тся средняя скорость
точки?
Средней		скоростью Vср						точки за
время ∆t называют
отношение
				=	∆r	.
		V		=	∆t	.
			ср		∆t
Средняя		скорость					совпадает			с
вектором ∆r . В о щем случае она зависит
	б
от времени осреднения ∆t.

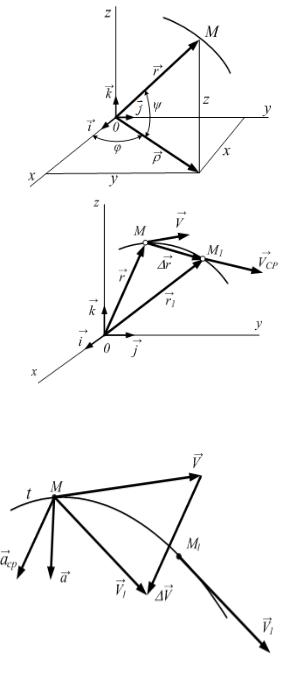
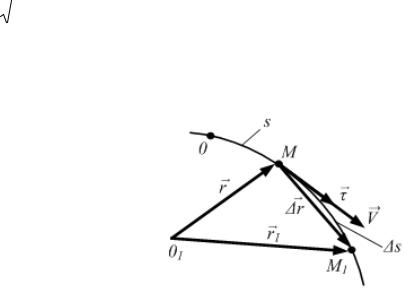
6. Как определяется среднее ускорение точки?

Пусть движущаяся точка М в момент времени t имеет скорость V .

В момент времени		t1 =t + ∆t	эта
	А
точка занимает положение М1, имея
скорость V1. Чтобы изобразить
приращение скорости		∆V за время
∆t, перенесём	вектор	скорости	V
			1
			Д
параллельно самому себе в точку М.				И
Средним ускорением точки аср
за время ∆t называют отношение
	∆V
aср = ∆t .
Среднее ускорение точки параллельно приращению скорости					∆V .
Среднее ускорение не имеет на траектории конкретной точки приложения
и изображено в точке М условно. В общем случае среднее ускорение
зависит от времени ∆t.

Ускорением точки a в момент времени t называют предел, к которому стремится среднее ускорение при ∆t, стремящемся к нулю, т.е.

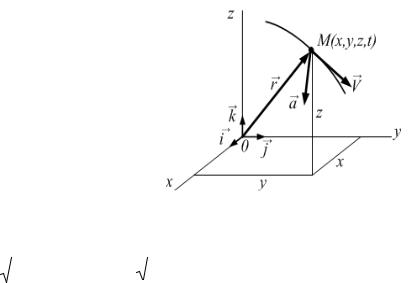
a =	lim	∆V	= dV .
	∆t→0	∆t	dt
Таким образом, ускорение точки равно первой производной по
времени от скорости точки.

С
7. Как определяется скорость точки при векторном способе задания?
Введём понятие действительной скорости точки V в момент времени
t, которая определяется как предел средней скорости, если промежуток
времени, за который определяется средняя скорость, стремится к нулю, т.е.
	V = lim ∆r = dr .

Так м образом, скорость точки равна первой производной по времени от её рад уса-вектора. Она направлена по касательной к траектории в

точки ∆Vt→=0 ∆t . dt dt

сторону дв жен я

равна

8. Как

определяется

величина ускорения точки при векторном способе

задания движения?

Для ускорения точки соответственно имеем

d 2r

= dt

= dt2 .

9. Как определяется скорость точки при

координатном способе задания?

Проекция вектора

скорости

на

какую-либо координатную ось равна

первой производной

по

времени

от

соответствующей

координаты

движущейся точки:

dх

Vx =

= х;Vy = dt

= y

; Vz = dt = z.

По проекциям определяют модуль скорости и направляющие

косинусы углов вектора скорости с осями координат:

V =

;

Vx2 +Vy2 +Vz2

x2 + y2 + z2

cos(V,i )

; cos(V,

j) =

;

cos(V,k ) =

Если точка движется в плоскости, то, выбрав оси координат Оx и Оy в

этой плоскости,

получим

z = const = 0

;

Vz = z = 0;

= y ;

Vx = x .

оответственно

V =

+ y

; cos(V ,i ) =

cos(V , j) =

;

Для прямолинейного движения точки координатную ось, например

Оx, направляют по траектории. Тогда

y = const = 0

z = const = 0 ,

следовательно, y = 0;

z = 0 .

Коорд нату точки, проекцию скорости и ее модуль определяют по

формулам

коорди

= x ,

V =Vx .

= f (t)

10. Как определяется величина ускорения точки при координатном

способе задан я дв жен я?

Вектор ускорен я точки представим через его проекции на оси

декартовой с стемы

нат, т.е.

а =

ахi +ay j +az k ,

где ах, ау, аz – проекц

вектора ускорения на координатные оси.

Согласно определению ускорения имеем

(Vxi

+Vy

j +Vz k )

= xi +

yj + zk.

Получаем формулы для проекций ускорения на оси декартовой

системы координат

ах =

= x;

у =

dVy

= y ;

аz

= z.

Проекция вектора ускорения на какую-либо координатную ось равна

второй производной по времениДот соответствующей координаты

движущейся точки.

Числовое значение ускорения и косинусы углов вектора ускорения с

осями координат определяют по формулам

а =

ах2 + а2у + аz2

x2 + y2 + z2 ;

cos(a,i ) =

;

cos(a,

;

cos(a,k ) =

При движении точки в плоскости осей Оx и Оy выбирают в этой же плоскости.

Тогда z=const=0; аz = z = 0.

Формулы для ускорения и его проекций на оси координат примут

вид

;

a = xi + yj

ах = х;

ау = у.

оответственно

а =

;

cos(a,i )

= a

; cos(a,

= a .

Для прямолинейного движения ось Оx направим по траектории

точки. Тогда у = const = 0; z = const = 0 и

ау

= у = 0 ; следовательно,

a = x .

11. Как определяется скорость точки при

дифф

естественном способе задания?

При дв жен

точки

её радиус-вектор

изменяется

течен ем

времени

и,

следовательно, является функцией двух

переменных

r (s,t)

. Определим скорость

точки,

спользуя

правило

еренц рован я

функций

двумя

переменными,

dr ds

V = dt

= ds dt

= ds s

= τs

=Vτ.

Касательный вектор

равный производной от радиуса-вектора

τ =

по дуговой координате,

направлен по касательной к кривой в точке М.

Величина V = s

называется алгебраической скоростью точки. Её можно

считать проекцией скоростиАна положительное направление касательной к

траектории, совпадающее с направлением единичного вектора

τ.

Модуль скорости точки в данный момент времени равен первой

производной от дуговой координаты точки по времени:

V = dt = s.

12. Как направлен и чему равен единичный вектор τ?

Единичный вектор

всегда направлен по касательной к траектории в

сторону возрастания дуговой координаты независимо от направления движения точки. Модуль этого вектора равен единице как предел отношения длины хорды ∆r к длине стягивающей дуги ∆s при стремлении её к нулю.

13. Дать определение нормальному и касательному ускорениям точки при

естественном способе задания.

Проекцию ускорения на положительное направление касательной, совпадающую с направлением единичного вектора τ, называют

касательным ускорением, а на главную нормаль, направленную по единичному вектору n , – нормальным ускорением.

Проекция ускорения на бинормаль, направленная по единичному

вектору b , равна нулю; следовательно, ускорение точки расположено в соприкасающейся плоскости с траекторией. В этой плоскости находятся

единичные векторы касательной и главной нормали.

14. Как определяется ускорение точки при естественном способе задания?

Разложим

ускорение

точки

по

естественным осям координат. Часть ускорения

aτ

называют

касательной

составляющей

нормали

ускорен я. Другую часть

называют

нормальной составляющей ускорения. Она

направлена в сторону вогнутости траектории,

т.е. в сторону

ед н чного вектора главной

n .

бn

Ускорен е точки при криволинейном движении

a = aτ + an .

Получ м формулы для проекций ускорения на естественные оси

aτ =

;

a =

V 2

;

a = 0 .

15. Чему равно полное ускорение точки при естественном способе

задания?

Дan

Учитывая ортогональность векторов

aτ и a , имеем полное ускорение

точки

aτ

tg α =

a =

+ a2

;

17.Каково направление касательного ускоренияИточки? ДвижениеНормальная16Касательнаяускоренноевогнутости

сторону касательной, т. е. по направлению единичного вектора τ, а приs < 0 – в отрицательную, противоположно τ.

При s > 0 и s > 0 вектор скорости и вектор касательной составляющей ускорения направлены в одну сторону – по τ. Движение точки является ускоренным в положительном направлении касательной к траектории.

При s < 0 и s < 0 вектор скорости и вектор касательной составляющей ускорения также имеют одинаковые направления и следовательно, движение точки является ускоренным в отрицательном направлении по касательной к траектории.

При s < 0 и s > 0 имеем замедленное движение точки в отрицательную сторону по касательной к траектории точки.

18. Чему равно касательное ускорение точки при координатном способе задания?

Если требуется определить касательное и нормальное ускорения при

координатном способе задания движения точки, то сначала по формулам

модулиaτ = =

определяют

скорости и ускорения точки:

;

= Vx

+Vy +Vz

= ax

+ ay

+ az .

огласно формуле

2Vx

dVx

+ 2Vy

dVy

+ 2Vz

dVz

Vx2 +Vy2 +Vz2

или aτ =

Vxax +Vyay +Vz az

Знак плюс, полученный в ответе после вычисления дроби,

соответствует ускоренному движению точки, а знак минус –

замедленному.

19. Чему равно нормальное ускорение точки при координатном способе

задания?

Vxax +Vyay +Vz az

V = Vx2 +Vy2 +Vz2 ; a = ax2 + a2y + az2 ; aτ =

Нормальное ускорение точки определяют по формуле

an =

a2 −aτ2

20. Расскажите о зависимости характера движения точки от значений её нормального и касательного ускорений в течение некоторого промежутка времени.

а) Если ускорения an = 0 ; aτ = 0 , то точка движется прямолинейно и

равномерно.

б) Если ускорения an ≠ 0 ; aτ = 0 , то точка движется криволинейно и равномерно.

Модуль её ускорения a = an =V 2ρ.

Если aτ = 0 в отдельный момент времени, то точка не движется

равномерно, а в этот момент времени модуль её скорости имеет экстремальное значение.

Например, при колебаниях маятника его скорость максимальна в вертикальном положении маятника. При экстремуме скорости ускорение в

этом положении маятника				aτ = 0 .
С
в)	Если ускорения an			= 0 ; aτ ≠ 0, то точка движется прямолинейно и
неравномерно. Модуль её ускорения a = aτ =						d 2s	.
		V 2				dt2
скорости
Если an =		ρ	= 0 в некоторый момент времени, то точка не движется
прямол нейно,		а проход т точку перегиба траектории (ρ = ∞) или модуль
её	обращается в нуль (например,					при изменении направления
	б
движен я точки V = 0), в этой точке скорость меняет знак.
г) Если ускорен я a				≠ 0 ; aτ ≠ 0, то точка совершает криволинейное
			n
неравномерное		дв жен е.			Модуль её ускорения a =			aτ2 + an2	. Если
направлен я векторов V				и	aτ совпадают, то движение ускоренное, в
			А
противном случае – замедленное.

21. Что называется равномерным движением точки?

Равномерным называют такое движение точки по траектории любой

формы, при котором		численная величина скорости всё время остаётся
постоянной: V = const .				Д
постоянной: V = const .
	dV
Тогда	aτ = dt =	0 ,	и	ускорение	точки равно		его			нормальному
ускорению a = an =V 2		ρ.
Найдём	уравнение		равномерного		криволинейного				движения. з
формулы V = ds получаем						И
формулы V = ds получаем				ds =Vdt . Пусть в начальный момент времени
	dt
(t0 = 0) точка находится от начала отсчёта на расстоянии s								0	. Тогда, взяв от
левой и правой частей равенства определённые интегралы в
соответствующих пределах,				получим s	ds = t	Vdt или	s − s		0	=Vt . Так как
				∫	∫				0
				s0	0

V = const , окончательно находим закон равномерного движения точки в виде

s = s0 +Vt .

22. Что называется равнопеременным движением точки?

Равнопеременным называют такое движение точки по траектории любой формы, при котором касательное ускорение остаётся постоянным:

aτ

= const .

23. Вывести закон равнопеременного движения точки.

Найдём закон равнопеременного движения, считая,

что

при

t0 = 0

s = s0 ; V =V0 , где V0 – начальная скорость точки.

По формуле dV = a

или

dV = a dt . Так как

a = const , то, взяв от

Вторично

a t2

обеих частей последнего равенства интегралы в соответствующих

пределах, получ м

V =V +a t .

Формулу представ м

виде

ds =V + a t

или

ds =V dt +a tdt .

точки:

нтегр руя, найдём уравнение равнопеременного движения

s = s

+V t +

24. Что называется равноускоренным и равнозамедленным движением точки?

Если при движении точки модуль скорости возрастает, то движение

называется равноускоренным (aτ > 0),

а если убывает – равнозамедленным

(aτ < 0). Данное

утверждение

справедливо

при

движении

точки в

положительном направлении отсчёта дуговой координаты s .

26. Дайте определение радиусу кривизны.

Модуль вектора кривизны К есть величина, обратная радиусу

кривизны (радиусу кривой) в данной точке.
Направление вектора		K определяет вектор, который в пределе при
∆φ→0 совпадает с нормалью n .					И
∆φ→0 совпадает с нормалью n .			Д
Получим окончательно			Д
				1
			K =	ρn .
25. Дайте определение вектору кривизны.
Вектором кривизны K		кривой является
предел отношения
K = lim
K = lim	∆τ = dτ .
∆s→0	∆s	ds

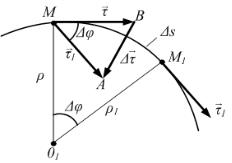
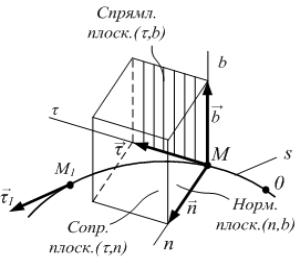
На рисунке в точках Μ и M1 показаны

касательные векторы, модули которых равны τ = τ1 =1.

Для оценки величины изменения вектора τ на дуге ∆s вектор τ1

перенесём в точку М. Тогда из векторного треугольника МАВ										∆τ = τ1 − τ.
В свою очередь ∆τ можно						выразить через ∆φ из треугольника МАВ:
∆τ =1 ∆ϕ.
Таким образом, модуль вектора кривизны
С							K = ∆ϕ.
К касательным векторам τ,							τ1	∆s
К касательным векторам τ,							τ1	на рисунке в точках М,	М1 проведены
нормали в в де отрезков					ρ,		ρ1,	которые пересекаются	в	точке	О1,
радиус							дуги ММ1. Величины ρ,		ρ1
называемой		центром		кр визны			дуги ММ1. Величины ρ,		ρ1	являются
ми кр в зны в точках М, М1.
Используя формулы геометрии и учитывая, что при ∆s → 0 ; ρ1 →ρ,
получим	∆s = ρ∆ϕ.
Тогда найдём K =				1 , где		ρ – радиус кривизны траектории.
				ρ
27.	Расскаж те			о	правиле
			А
построен	я	естественных				осей
координат.
Построимбв точке М кривой
естественные оси координат.
Первой		естественной				осью
является		касательная					τ.
Положительное			направление				Д
Положительное			направление			этой
оси совпадает			с направлением
единичного вектора касательной							τ,	И
направленного			в		сторону
возрастания дуги.
Перпендикулярно касательной оси τ располагается нормальная ось											n ,
направленная в сторону вогнутости кривой – к центру кривизны.
Оси τ и n образуют соприкасающуюся плоскость, которая находится
в плоскости кривой ММ1, т.е. в плоскости, образованной векторами τ,											τ 1,

при ММ1 →0 . Через ось n перпендикулярно оси τ проходит нормальная

плоскость, в которой перпендикулярно осям τ и n расположена вторая нормаль b, называемая бинормалью.

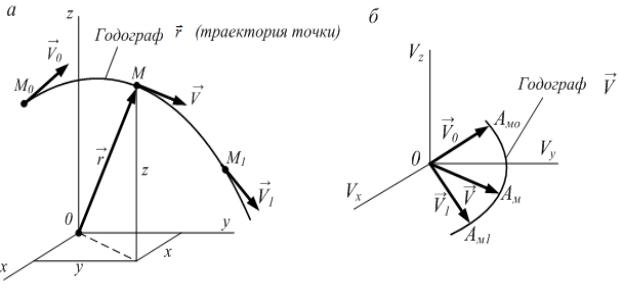
28. Расскажите о естественных осях координат.

Три взаимно перпендикулярные оси τ, n , b, положительные направления которых совпадают с направлениями единичных векторов τ,

n , b , называют естественными осями координат. Эти оси образуют в точке М естественный трёхгранник.

При движении точки М по кривой естественный трёхгранник движется вместе с точкой как твёрдое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.

Правило определения правой системы координат заключается в том,

чтобы, смотря навстречу вектору b , видеть поворот вектора τ к вектору n против вращения часовой стрелки.

Термин правая система координат заимствован из физики: вправо

происходит вращение буравчика, остриё которого совпадает с вектором b при повороте оси τ к оси n .

29. Нап ш те формулу для определения радиуса кривизны траектории
траектории
движен я точки.
СРад ус кр в зны		находим из формулы
		ρ =	V 2
			.
			an
б
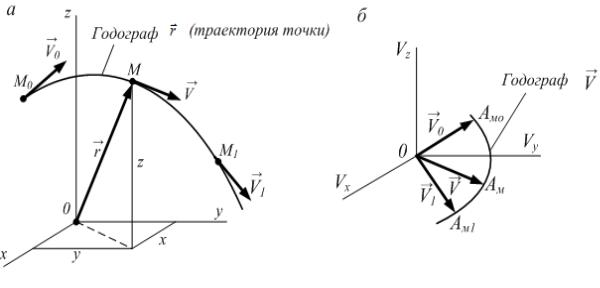
30. Что называется годографом вектора скорости?
Годографом вектора скорости является линия, на которой
располагаются концы вектора скорости в различные моменты времени,
если их начала совмест	ть в одной о щей точке.
А
31. Как строится годограф вектора скорости?
		Д
Для построения			И
	годографа вектора скорости выбирают точку,

например О (рис. б), и начала векторов скорости для различных моментов времени помещают в эту точку, не изменяя их направлений. Каждой точке М траектории (рис. а) соответствует своя изображающая точка АМ на

годографе вектора скорости (см. рис. б).

Масштаб скоростей при построении годографа вектора скорости может быть выбран отличным от масштаба для скоростей, изображаемых в

точках траектории. При движении точки М по траектории

соответствующая ей изображающая точка АМi	движется по годографу
вектора скорости.
При равномерном движении точки по прямой годографом вектора
скорости является одна точка, при неравномерном движении – отрезок
этой прямой.
С
32. Назовите параметрические уравнения годографа вектора скорости.
Пусть известны уравнения движения	точки в декартовых

координатах.

На р сунке а показаны траектория точки и несколько векторов
скорости			б показан годограф
скорости для разных моментов времени, а на рисунке
вектора скорости дв	жен я точки.
Точке М (x, y, z) на траектории соответствует точка АM (Vx ,Vy ,Vz ) на
годографе вектора	.
б
	А
	Д
Координаты точки АM , согласно определению годографа, выражают
		И
через проекции скорости на ортогональные оси координат ОVx Vy Vz по
формуле	j +Vz k , где Vx (t) = x ;	Vy (t) = y ;	Vz (t) = z .
V =Vxi +Vy

Представленные выражения проекций вектора скорости являются параметрическими уравнениями годографа вектора скорости.

<<< < Предыдущая 1 2 3 4 5 67 / 207 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20213.84 Mб72187.pdf
#
07.01.20213.85 Mб12188.pdf
#
07.01.20213.85 Mб162189.pdf
#
07.01.2021356.57 Кб0219.pdf
#
07.01.20213.86 Mб112190.pdf
#
07.01.20213.86 Mб152191.pdf
#
07.01.20213.87 Mб72192.pdf
#
07.01.20213.88 Mб22193.pdf
#
07.01.20213.89 Mб202194.pdf
#
07.01.20213.91 Mб82195.pdf
#
07.01.20213.92 Mб12196.pdf