
- •ВВЕДЕНИЕ
- •1. СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА
- •1.1. Рекомендации для проведения практического занятия
- •1.3. Контрольные вопросы для тестирования студентов
- •2. СИСТЕМА СХОДЯЩИХСЯ СИЛ
- •2.2. Методические рекомендации к решению задач
- •2.3. Контрольные вопросы для тестирования студентов
- •3. ТЕОРИЯ ПАР СИЛ
- •3.1. Рекомендации для проведения практического занятия
- •3.2. Контрольные вопросы для тестирования студентов
- •4. ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ
- •4.1. Рекомендации для проведения практического занятия
- •4.2. Методические рекомендации к решению задач
- •4.3. Контрольные вопросы для тестирования студентов
- •5. ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ В ПРОСТРАНСТВЕ
- •5.1. Рекомендации для проведения практического занятия
- •5.2. Методические рекомендации к решению задач
- •5.3. Контрольные вопросы для тестирования студентов
- •6. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
- •6.1. Рекомендации для проведения практического занятия
- •6.2. Методические рекомендации к решению задач
- •6.3. Контрольные вопросы для тестирования студентов
- •7. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- •7.1. Рекомендации для проведения практического занятия
- •7.2. Методические рекомендации к решению задач
- •7.3. Контрольные вопросы для тестирования студентов
- •8. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- •8.1. Рекомендации для проведения практического занятия
- •8.3. Контрольные вопросы для тестирования студентов
- •9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
- •9.1. Рекомендации для проведения практического занятия
- •9.2. Методические рекомендации к решению задач
- •9.3. Контрольные вопросы для тестирования студентов
- •10. МГНОВЕННЫЙ ЦЕНТР СКОРОСТЕЙ
- •10.1. Рекомендации для проведения практического занятия
- •10.2. Методические рекомендации к решению задач
- •10.3. Контрольные вопросы для тестирования студентов
- •11. ДИНАМИКА ТОЧКИ
- •11.1. Рекомендации для проведения практического занятия
- •11.2. Методические рекомендации к решению задач
- •11.3. Контрольные вопросы для тестирования студентов
- •12. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- •12.1. Рекомендации для проведения практического занятия
- •12.2. Методические рекомендации к решению задач
- •12.3. Контрольные вопросы для тестирования студентов
- •13. ТЕОРЕМА ОБ ИЗМЕНЕНИИ ГЛАВНОГО МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- •13.1. Рекомендации для проведения практического занятия
- •13.2. Методические рекомендации к решению задач
- •13.3. Контрольные вопросы для тестирования студентов
- •14. МОМЕНТЫ ИНЕРЦИИ ТЕЛА И МЕХАНИЧЕСКОЙ СИСТЕМЫ
- •14.1. Рекомендации для проведения практического занятия
- •14.2. Методические рекомендации к решению задач
- •14.3. Контрольные вопросы для тестирования студентов
- •15. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ
- •15.1. Рекомендации для проведения практического занятия
- •15.3. Контрольные вопросы для тестирования студентов
- •16. ПРИНЦИП ДАЛАМБЕРА
- •16.1. Рекомендации для проведения практического занятия
- •16.2. Методические рекомендации к решению задач
- •16.3. Контрольные вопросы для тестирования студентов
- •17. ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
- •17.1. Рекомендации для проведения практического занятия
- •17.3. Контрольные вопросы для тестирования студентов
- •18. ТЕОРИЯ УДАРА
- •18.1. Рекомендации для проведения практического занятия
- •18.2. Методические рекомендации к решению задач
- •18.3. Контрольные вопросы для тестирования студентов
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

14. МОМЕНТЫ ИНЕРЦИИ ТЕЛА И МЕХАНИЧЕСКОЙ СИСТЕМЫ
14.1. Рекомендации для проведения практического занятия
Цели занятия: познакомиться с особенностями применения общих теорем д нам ки при изучении движения твёрдого тела, научиться составлять д фференц альные уравнения поступательного, вращательного
плоскопараллельного движения твёрдого тела и использовать их при |
||||||
дифференцрован я скалярных и векторных функций скалярного |
||||||
решен |
первой |
второй |
задач |
динамики, |
познакомиться |
с |
Сальными уравнениями вращательного движения твёрдого тела |
||||||
вокруг неподв жной оси и движения твёрдого тела вокруг неподвижной |
||||||
точки. |
б |
|
|
|
||
Перед |
зучен ем данной |
темы |
рекомендуется повторить |
со |
||
студентами следующ е вопросы из курса математики: основные правила |
||||||
аргумента одной переменной; определенные и неопределенные интегралы; |
||||||
дифференц альные |
А |
их |
||||
уравнения с |
разделяющимися |
переменными и |
||||
интегрирование; линейные дифференциальные уравнения с постоянными коэффициентами (однородные и неоднородные) и их интегрирование, задача Коши в теории дифференциальных уравнений; скалярное произведение векторов и его свойства.
Следует повторить со студентамиДследующие вопросы из раздела
«Кинематика»: кинематика твердого тела (определение скоростей точек твердого тела при различных видах его движения – поступательном, вращательном, плоскопараллельном), вращение твёрдого тела вокруг неподвижной точки, углы Эйлера, кинематические уравнения Эйлера.
1.Уметь применять общие теоремы динамикиИдля изучения движения твёрдого тела.
2.Уметь составлять дифференциальные уравнения поступательного, вращательного и плоскопараллельного движения твёрдого тела и использовать их при решении первой и второй задач динамики.
3.Уметь определять моменты инерции диска, кольца, стержня, пластины.« Следует повторить со студентами следующие вопросы из раздела
104
14.2. Методические рекомендации к решению задач
Для решения задач динамики плоскопараллельного движения твёрдого тела рекомендуется:
1. |
Изобразить твёрдое тело, движение которого рассматривается, в |
текущем положении. |
|
С |
|
2. |
Выбрать и изобразить три системы координат: одну неподвижную и |
две подвижные (одну движущуюся поступательно и вторую жёстко |
|
связанную с твёрдым телом) с началами в центре масс твёрдого тела. |
|
3. |
Изобраз ть на расчётной схеме все внешние силы, приложенные к |
добавить |
|
твёрдому телу. |
|
4. |
остав ть д фференциальные уравнения движения твёрдого тела и |
|
к н м уравнен я связей. |
5. |
Если это нео ходимо, проинтегрировать дифференциальные |
уравнен я дв жен я определить искомые величины.
В некоторых случаях для решения задач оказывается более целесообразным вместо одного из дифференциальных уравнений движен я твёрдого тела спользовать теорему об изменении кинетической энергии механ ческой с стемы.
Задачи по при лижённой теории гироскопов можно разбить на два |
|
типа: |
б |
1.Определение прецессии оси трёхстепенного гироскопа по заданным внешним силам и угловой скорости собственного вращения ротора гироскопа.
2.Определение гироскопических реакций подшипников по известной
угловой скорости принудительной прецессии и угловой скорости собственного вращения ротора гироскопа.А
Задачи |
первого |
типа |
рекомендуется |
решать |
в |
такой |
последовательности: |
|
Д |
|
|||
1.Проверить, имеет ли гироскоп или гироскопическая система три степени свободы.
2.Выбрать две системы координат – подвижную и неподвижную, совместив их начало с неподвижной точкой гироскопа и направив одну из осей подвижной системы по оси вращения ротора.
3.Изобразить на рисунке внешние силы, приложенные к гироскопу.
4.Определить главный момент внешних сил относительно неподвижной точки.
5.Найти главный момент количеств движения гироскопа относительно неподвижной точки.
6.Применив теорему Резаля, определить движение оси гироскопа.
Взадачах, связанных с определением гироскопических давлений (гироскопических реакций опор), рекомендуется:И
105
|
1. Изобразить на рисунке векторы угловой скорости собственного |
|||||||||||||||||||||||||||||||||||||
вращения гироскопа и главного момента количеств движения. |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
2. Определить и изобразить на рисунке вектор угловой скорости |
|||||||||||||||||||||||||||||||||||||
прецессии оси гироскопа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
3. Найти гироскопический момент (главный момент внешних сил). |
|
||||||||||||||||||||||||||||||||||||
|
4. Определить направления и модули гироскопических давлений на |
|||||||||||||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
опоры (гироскопических реакций опор). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
14.3. Контрольные вопросы для тестирования студентов |
|
|
||||||||||||||||||||||||||||||||||
точки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
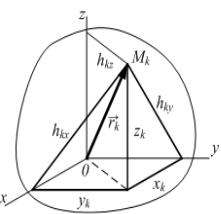
1. Что называют моментом инерции материальной точки и системы |
|||||||||||||||||||||||||||||||||||||
материальных точек относ тельно плоскости? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Момент |
|
нерц |
|
|
|
|
материальной |
точки |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
относ тельно плоскости есть произведение |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
массы |
|
|
|
|
|
на |
|
квадрат |
расстояния |
|
до |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
плоскости. |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Для |
|
|
|
|
M k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
JOyz = mk xk2 ; JOxz = mk yk2 ; |
JOxy = mk zk2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Для с стемы точек |
|
|
|
|
|
y2 ; J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
J |
Oyz |
= ∑m |
k |
x2 |
; J |
Oxz |
= ∑m |
k |
Oxy |
= ∑m |
k |
z2 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
оси? |
2. Что называют моментом инерции материальной точки относительно |
|||||||||||||||||||||||||||||||||||||
Момент инерции точки относительно оси есть произведение массы |
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
точки на квадрат расстоянияАот точки до оси. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Согласно определению получим для точки M k |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
J |
x |
= m |
k |
h2 |
; J |
y |
= m |
h2 ; |
|
J |
z |
= m |
k |
h2 ; |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
kx |
|
|
|
|
k ky |
|
|
|
|
|
kz |
|
|
|
|
|
|
|||||||||
|
для системы точек J |
|
|
|
= |
|
n |
m |
|
2 |
|
|
|
n |
|
|
|
|
2 |
|
|
n |
|
2 |
. |
|||||||||||||
|
|
|
|
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
x |
|
|
hД; J = ∑ m h ; J = ∑ m h |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
k kx |
y |
|
k = 1 |
k ky |
z |
k |
= 1 |
k kz |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Учитывая, что h2 |
= z |
2 |
+ y2 |
; |
|
|
h2 |
= x2 |
+ z |
2 ; |
|
h |
2 |
|
= x2 |
+ y2 , |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
kx |
|
|
|
k |
|
|
k |
|
|
|
ky |
k |
|
k |
|
kz |
k |
|
k |
|
|
|
|
||||||
можно записать |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
n |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
n |
|
2 |
|
2 |
|
|
|
|
n |
|
|
|
|
|
|
||||
|
J x |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
И2 2 |
||||||||||||||||
|
= ∑ mk (yk |
+ zk ); J y |
|
∑ mk (xk + zk ); |
J z |
= |
∑ |
mk |
(xk |
+ yk ) . |
|
|||||||||||||||||||||||||||
|
|
|
k = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
|
|
|
|
||||||
3. Что называют полярным моментом инерции тела относительно центра?
Полярным моментом инерции тела относительно центра называют сумму произведений масс точек тела на квадрат расстояний от точек до центра, т.е.
106
|
|
|
|
|
|
J |
|
= |
п |
r2 |
= |
п |
|
(x2 + y |
2 |
+ z2 ) . |
||
|
|
|
|
|
|
o |
∑m |
∑m |
k |
|||||||||
|
|
|
|
|
|
|
|
k=1 |
k k |
|
k =1 |
k |
|
k |
k |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полярный момент инерции тела равен половине суммы моментов |
||||||||||||||||||
инерции тела относительно осей координат. |
|
|
|
|
||||||||||||||
С |
|
|
|
|
|
|
2Jo = J x + J y + J z . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для сплошных твердых тел уравнение можно заменить интегралом |
||||||||||||||||||
|
|
|
|
|
|
|
|
Jo = ∫(x2 + y2 + z2 )dm . |
|
|
||||||||
Центробежнымимоментами инерции называют величины J xy , J yz , |
||||||||||||||||||
4. Что называют моментом инерции твердого тела относительно |
||||||||||||||||||
плоскости, оси точки? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Моментом |
нерц |
|
|
|
твердого тела относительно плоскости называют |
|||||||||||||
скалярную вел ч ну, равную сумме произведений массы каждой точки |
||||||||||||||||||
тела на квадрат расстоян |
я от этой точки до плоскости. |
|
||||||||||||||||
|
б |
|
|
|
|
|||||||||||||
5. Дайте определен |
|
|
центро ежным моментам инерции? |
|||||||||||||||
J zx , определяемые равенствами |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
А |
|
||||||||||||
|
J xy = ∑mk xk yk ; |
J yz = ∑mk yk zk ; |
J zx |
= ∑mk zk xk , |
||||||||||||||
где mk – массы точек; |
|
xk , yk , zk – их координаты. |
|
|
||||||||||||||
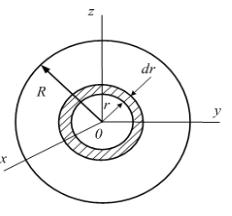
6. Как вычисляются осевые моменты инерции однородного круглого диска? |
||||||||||||||||||
Имеем |
тонкий |
|
|
|
|
|
|
|
Д |
|||||||||
|
|
однородный |
диск |
|
|
|
|
|||||||||||
радиусом R и массой m. Вычислим его |
|
|
|
|
||||||||||||||
момент инерции Jo |
относительно точки O. |
|
|
|
|
|||||||||||||
Этот момент инерции для тонкого диска |
|
|
|
|
||||||||||||||
совпадает с моментом инерции Jх |
|
|
|
|
||||||||||||||
относительно координатной оси Оx, |
|
|
|
|
||||||||||||||
перпендикулярной |
|
|
|
плоскости |
|
диска. |
|
|
|
|
||||||||
Разобьем диск на концентрические полоски |
|
|
|
|
||||||||||||||
шириной dr, принимаемые в пределе за |
|
|
|
|
||||||||||||||
материальные окружности. |
|
|
|
|
|
|
|
|
|
|
||||||||
Масса полоски равна ее площади 2πrdr , |
умноженной на удельную |
|||||||||||||||||
плотность |
ρ = |
m |
, |
|
|
т.е. |
dm =ρ 2πrdr . |
МоментИодной полоски |
||||||||||
πR2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
относительно точки О равен r2dm . Для всего диска |
|
|||||||||||||||||
|
|
Jo = |
m |
|
|
|
|
|
R |
|
|
|
|
4 |
= mR |
2 |
||
|
|
∫r2dm |
=ρ 2π |
∫r3dr =ρ 2π R |
|
. |
||||||||||||
|
|
|
|
o |
|
|
|
|
|
|
o |
|
|
|
4 |
2 |
|
|
Таким образом,
107
|
|
|
Jx = Jo = |
mR2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
Для осей координат Oz и Oy, расположенных в плоскости диска, в |
||||||||||||||||
силу симметрии J z = J y . Тогда |
J z = J y = |
J |
o |
= |
mR |
2 |
. |
|
|
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||
С |
|
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|||
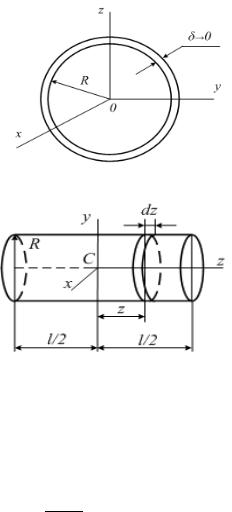
7. Как вычисляются осевые моменты |
|
|
|
|
|
|
|
|
|
|||||||
инерции тонкого кольца? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае тонкого кольца, имеющего |
|
|
|
|
|
|
|
|
|
|||||||
форму ц л ндра с малой толщиной стенки |
|
|
|
|
|
|
|
|
|
|||||||
цилиндра, масса которого m, радиус R и |
|
|
|
|
|
|
|
|
|
|||||||
δ → 0 , масса |
матер |
ала распределена |
|
по |
|
|
|
|
|
|
|
|
|
|||
ободу ц л ндр |
ческого кольца, имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|||
J x = Jo = mR2 ; |
J y = J z = 1 mR2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Как выч сляются осевые моменты инерции цилиндра? |
|
|
||||||||||||||
Для |
круглого однородного |
прямого |
|
|
|
|
|
|
|
|
|
|||||
длина l , |
выч сл м |
сначала его |
момент |
|
|
|
|
|
|
|
|
|
||||
инерции |
относ тельно продольной оси |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
А |
|
|
|||||||||||
симметрии Oz. Для этого разо ьем цилиндр |
|
|
|
|
|
|
|
|
|
|||||||
плоскостямиб, перпендикулярными оси Oz, |
|
|
|
|
|
|
|
|
|
|||||||
на тонкие диски массой dm и толщиной dz. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
Д2 |
dm. |
|||||||||||
Для такого диска момент инерции относительно |
оси Oz равен |
2 |
||||||||||||||
Расчетная |
схема показывает, что |
масса |
всего |
цилиндра образуется из |
||||||||||||
суммы элементарных дисков, т.е. масса цилиндра m = ∑dm .
Формула момента инерции цилиндра относительно его оси симметрии
2
совпадает с формулой момента инерции диска JИz = mR .
Формулы моментов инерции цилиндра для осей Оx, Оy, Jx=Jy совпадают с соответствующей формулой момента инерции для прямого стержня:
JCx = JCy = ml2 .
12
9. Какое тело называется гироскопом?
Гироскопом называют симметричное твердое тело, имеющее одну неподвижную точку, быстро вращающееся вокруг собственной оси. В технике применяют гироскопы, у которых центр тяжести находится на оси материальной симметрии.
108
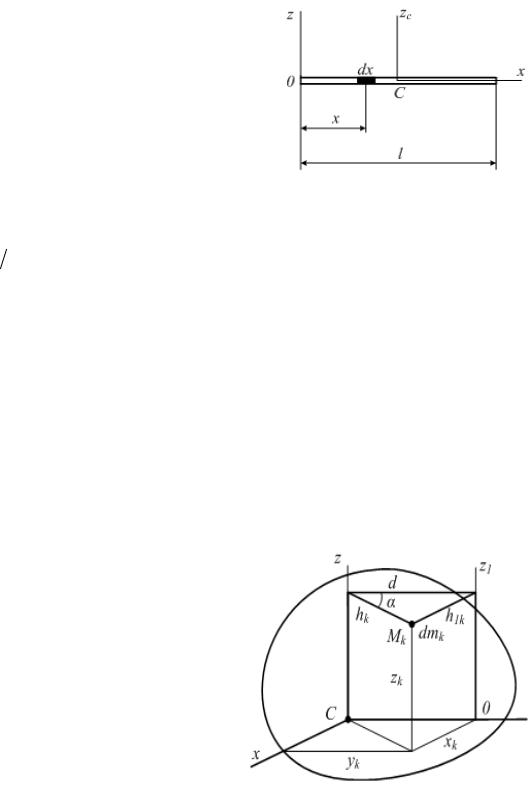
10. Как вычисляются осевые моменты инерции однородного стержня?
Имеем |
|
тонкий |
|
|
однородный |
|
|
|||||||||||
стержень длиной l и массой m. |
|
|
||||||||||||||||
Направим по стержню ось Ox. |
|
|
||||||||||||||||
Вычислим |
момент |
инерции |
|
стержня |
|
|
||||||||||||
относительно оси Oz, проходящей |
|
|
||||||||||||||||
перпендикулярно |
|
стержню |
через |
его |
|
|
||||||||||||
торец. |
огласно определению момента |
|
|
|||||||||||||||
инерции сплошного |
тела относительно |
|
|
|||||||||||||||
оси имеем |
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
||
|
|
|
|
Joz = |
∫ x2dm |
|
|
|
|
|
||||||||
|
|
|
|
= ρ∫ x2dx , т. к. dm = ρdx , |
|
|||||||||||||
С |
|
|
|
|
(l) |
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где ρ = m l |
– удельная плотность стержня. |
|
|
|||||||||||||||
Выч сляя |
нтеграл, получаем |
|
|
|
||||||||||||||
|
|
|
m l |
|
2 |
|
|
|
m l3 |
|
|
|
ml2 |
, таким образом, Joz = |
ml2 |
|||
иJoz = l ∫ x dx = l 3 = |
3 |
|
3 . |
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналог чным о разом можно получить момент инерции стержня для |
||||||||||||||||||
его центральной оси z |
|
: |
J |
|
= |
ml2 |
. |
|
|
|||||||||
C |
CZ |
|
|
|
||||||||||||||
|
|
б12 |
|
|
||||||||||||||
11. Чему равен момент инерции относительно параллельных осей. Теорема |
||||||||||||||||||
Гюйгенса-Штейнера? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Существует связь между моментами инерции тела относительно |
||||||||||||||||||
параллельных осей |
(теорема Гюйгенса-Штейнера), одна из которых |
|||||||||||||||||
|
|
|
|
|
|
|
А |
|
||||||||||
проходит через центр масс. |
|
|
|
|
|
|
|
|
|
|||||||||
Теорема. Момент инерции тела |
|
|
||||||||||||||||
JOz1 относительно некоторой оси Oz1 |
|
|
||||||||||||||||
равен |
сумме |
момента |
|
инерции |
JCz |
|
|
|||||||||||
тела |
относительно |
|
оси |
|
|
Cz, |
|
|
||||||||||
проходящей |
через |
|
|
|
центр |
|
|
|
Д |
|||||||||
|
|
|
|
|
|
масс |
И |
|||||||||||
параллельно |
данной |
|
оси, |
|
|
и |
||||||||||||
произведения массы тела на квадрат |
||||||||||||||||||
расстояний |
|
|
между |
|
|
осями: |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12. Как вычисляются осевые моменты инерции однородной треугольной пластины?
109
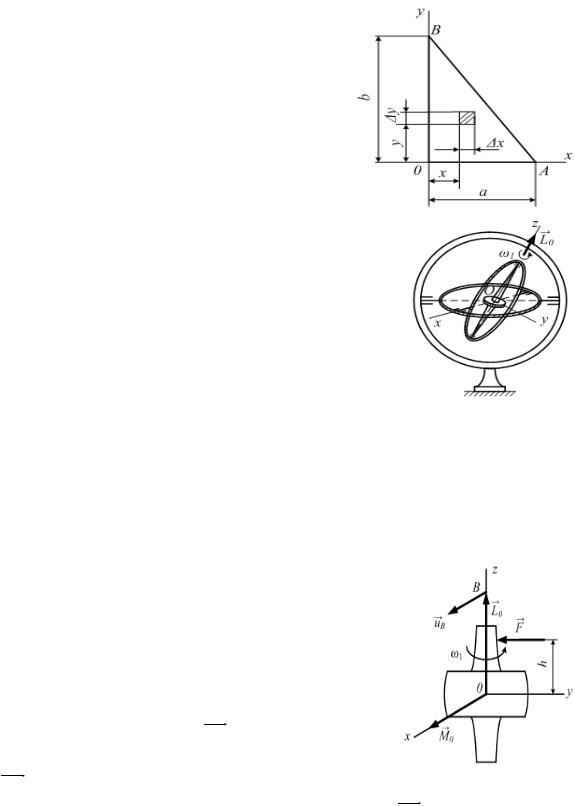
J x = |
mb2 |
; J y = |
ma2 |
. |
|
6 |
6 |
||||
|
|
|
|||
13. Что называется радиусом инерции? |
|||||
Радиусом инерции тела, например ix , |
|
называют линейную величину, квадрат |
|
С |
|
которой, |
умноженный на массу тела, равен |
моменту |
инерции тела относительно |
соответствующей оси координат: |
J |
x |
= i |
2m . |
||||||
|
|
|
|
|
|
|
|
|
x |
|
14. Какой г роскоп называется свободным? |
||||||||||
В |
г роскоп ческ х |
|
приборах |
гироскопы |
||||||
обычно закрепляют в кольцевом подвесе так, что |
||||||||||
любом повороте г роскопа его центр тяжести |
||||||||||
остается неподв жным. Такой гироскоп называется |
||||||||||
свободным. |
|
|
|
|
|
|
|
|
||
при15. В чём состо основное свойство свободного |
||||||||||
гироскопа? |
|
|
|
|
|
|
|
|
||
Пр меняемые в технике гироскопы имеют большую угловую |
||||||||||
скорость |
|
|
|
вращения ω1 вокруг своей оси симметрии. Если |
||||||
|
собственного |
|||||||||
тело вращается вокруг неподвижной оси Оz, являющейся осью симметрии |
||||||||||
тела, то вектор |
L0 кинетического момента совпадает с осью вращения: |
|||||||||
L0 = Lz = J zcω1, где J zc |
– момент инерции гироскопа относительно его оси |
|||||||||
симметрии. Ось свободного гироскопа сохраняет неизменное направление |
||||||||||
в пространстве по отношениюАк инерциальной (звездной) системе отсчета. |
||||||||||
Это важное свойство гироскопа используется |
||||||||||
при конструировании гироскопических приборов. |
||||||||||
|
|
|
|
|
|
|
|
Д |
||
16. Сформулируйте теорему Резаля. |
|
|||||||||
Пусть на ось быстро вращающегося гироскопа |
||||||||||
начинает |
действовать |
сила |
|
момент которой |
||||||
F , |
||||||||||
относительно центра О равен по модулю M0 = Fh. |
||||||||||
По теореме моментов |
|
|
|
|
|
|
И |
|||
|
|
dL |
|
|
d(OB) |
|
|
|
||
|
|
0 |
= M0 или |
|
|
= M0 , |
||||
|
dt |
|
dt |
|||||||
где OB – вектор, совпадающий с вектором L0 .
Отсюда, учитывая, что производная от вектора OB по времени равна скорости uB точки В, то uB = M0 . Равенство указывает, что скорость
конца вектора кинетического момента свободного гироскопа относительно центра О равняется по модулю и по направлению главному моменту
110
внешних сил относительно того же центра (теорема Резаля). Следовательно, точка В, а с нею и ось гироскопа будут перемещаться
параллельно вектору М0 . В результате находим, что если на ось быстро вращающегося гироскопа подействует сила, то ось начнет отклоняться не в
|
сторону действия силы, а по направлению, которое имеет |
вектор М0 |
|||||||||||
|
момента этой силы относительно неподвижной точки О гироскопа, т. е. |
||||||||||||
|
перпендикулярно силе. Из равенства следует также, что когда действие |
||||||||||||
|
силы F прекращается, |
то М0 , а следовательно, |
uB |
обращаются в нули и |
|||||||||
|
ось гироскопа останавл |
вается. |
|
|
|
|
|
|
|
||||
|
движен |
|
|
|
|
|
|
|
|||||
|
17. Что является мерой инертности при поступательном и вращательном |
||||||||||||
Сях? |
|
|
|
|
|
|
|
|
|||||
|
При поступательном движении твёрдого тела так же, как и при |
||||||||||||
|
движен |
матер альной точки, |
мерой инертности |
является |
масса. При |
||||||||
|
|
б |
|
его |
инертности является |
||||||||
|
вращательном |
дв жен |
твёрдого тела мерой |
|
|||||||||
|
момент |
нерц |
|
относ тельно оси вращения. |
|
|
|
|
|
||||
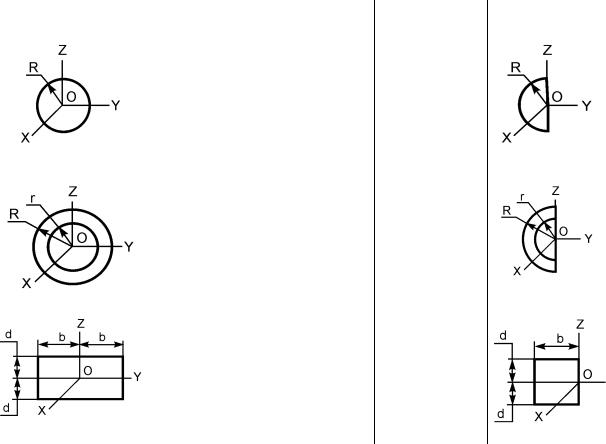
|
18. Расскаж те о моментах инерции однородных пластин. |
|
|
||||||||||
|
|
|
|
|
А |
|
|
||||||
|
|
|
Осевые моменты инерции однородных пластин |
||||||||||
|
Форма тела |
|
|
JOX |
|
JOY |
|
|
JOZ |
Форма тела |
|
||
|
|
|
|
|
|
m·R2/2 |
|
Д |
|
|
|||
|
|
|
|
|
|
|
m·R2/4 |
|
m·R2/4 |
|
|
||
|
|
|
|
|
m·(R2–r2)/2 |
|
m·(R2–r2)/4 |
И |
|
||||
|
|
|
|
|
|
|
m·(R2–r2)/4 |
|
|
||||
|
|
|
|
|
m·(b2+d2)/3 |
|
m·d2/3 |
|
|
m·b2/3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
111
