Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2191.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

3.86 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

15. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МЕХАНИЧЕСКОЙ СИСТЕМЫ

15.1. Рекомендации для проведения практического занятия

Цели занят я: выяснение области применения теоремы об изменении

кинетической энерг	при исследовании поведения механических систем,
приобретен е навыков составления дифференциальных уравнений
движен я механ ческ х систем с одной степенью свободы с помощью
Стеоремы об зменен	к нетической энергии в дифференциальной форме,
освоен е метод ки	пр менения теоремы об изменении кинетической

энергииПеред зучен ем данной темы рекомендуется повторить со студентами следующ е вопросы из курса математики: основные правила

в конечной форме для получения первых интегралов

дифференц альных уравнений движения механических систем.

б аргумента одной переменнойА, определенные и неопределенные интегралы;

дифференц рован я скалярных и векторных функций скалярного

дифференциальные уравнения с разделяющимися переменными и их интегрирование; линейные дифференциальные уравнения с постоянными коэффициентами (однородные и неоднородные) и их интегрирование; задача Коши в теории дифференциальных уравнений, скалярное произведение векторов и его свойстваД.

Следует повторить со студентами следующие вопросы из раздела

«Кинематика»: способы задания движения материальной точки, определение скорости и ускорения точки при векторном, координатном и естественном способах задания движения точки, естественные оси,

1.Владеть понятиями «кинетическая энергияИматериальной точки» и «кинетическая энергия механической системы».

2.Уметь вычислять кинетическую энергию твердого тела при поступательном, вращательном и плоскопараллельном его движениях, аестественный трехгранник, кинематика твердого тела (определение

также кинетическую энергию механических систем, состоящих из тел, совершающих перечисленные движения.

3. Владеть понятиями «элементарная работа силы», «работа силы на конечном перемещении» и «мощность силы».

112

4. Знать все формулы, необходимые для вычисления элементарной работы, полной работы и мощности силы, и уметь их применять при решении конкретных задач.

5. Уметь выводить теорему об изменении кинетической энергии механической системы в различных формах и формулировать ее

содержание.
С
6. Знать, как записывается теорема об изменении кинетической
энергии для неизменяемой механической системы. Свободно применять
теорему в разл чных ее формах к решению конкретных задач.
7. Владеть понят ями,		связанными с потенциальным силовым полем
силовая
(	функц я, работа	потенциальной силы, поверхности уровня,
потенц альная энерг я, полная механическая энергия и условия ее
сохранен я).
	15.2. Метод ческие рекомендации к решению задач
	б
Д фференц альная форма теоремы об изменении кинетической
энергии	механ ческой	системы используется для составления

дифференц ального уравнения движения систем с одной степенью свободы и, в частности, для нахождения ускорения движущихся тел. Эта форма может также использоваться для составления дифференциальных уравнений движения систем с несколькими степенями свободы совместно с другими общими теоремами динамики.

Конечная формаАтеоремы об изменении кинетической энергии механической системы позволяет получить первый интеграл дифференциальных уравнений движения в тех случаях, когда можно вычислить сумму работ внешних сил на конечном перемещении системы

без знания закона её движения.

Теорема об изменении кинетическойДэнергии в случаях, когда движущаяся механическая система является неизменяемой, позволяет исключить из рассмотрения все неизвестные внутренние силы, а при наложенных на систему идеальных, стационарных связях и неизвестные

реакции внешних связей.

При составлении дифференциального уравнения движения системы
следует:	И

1.Убедиться в том, что система имеет одну степень свободы.

2.Выбрать координату, относительно которой будет составляться уравнение движения.

3.Записать теорему об изменении кинетической энергии в дифференциальной форме.

113

4. Вычислить кинетические энергии отдельных тел системы. Кинетическую энергию системы вычислить как сумму кинетических энергий отдельных тел.

5. Угловые скорости тел системы и линейные скорости их центров масс выразить через заданную скорость. В результате кинетическая энергия механической системы также будет представлена как функция

Сэтого независимого параметра.

6. Вычислить производную по времени от кинетической энергии системы.

7. Изобраз ть на расчётной схеме все внешние силы, действующие на механическуюНайтис стему. Вычислить сумму мощностей внешних сил.

8. остав ть д фференциальное уравнение движения, используя для этого теорему об зменении кинетической энергии в дифференциальной

форме.

9. Задать начальные условия движения механической системы.

10. обобщее решение дифференциального уравнения движения.

11. Определ ть по начальным условиям постоянные интегрирования.

12. Подстав в значения постоянных интегрирования в общее решение

дифференц ального уравнения, найти закон движения механической системы. А

Теорема изменении кинетической энергии механической системы в конечной (интегральной форме) применяется, например, к решению задач в следующей постановке: механическая система, находящаяся в покое, под действием внешних сил приходит в движение. За некоторое время одно из тел системы перемещается на заданное расстояние.

Найти скорости, приобретённые телами системы. Порядок решения данной задачи следующий:

1.Убедиться в том, что механическая система имеет одну степень свободы.

2.Выбрать координату, с помощью которой будет определяться положение системы.

3.Записать теорему об изменении кинетической энергии механической системы в конечной форме, положив значение кинетической энергии механической системы в начальный момент времени равным нулю.

4.Изобразить на рисунке систему в начальном и конечном положениях. Вычислить кинетическую энергию системы в конечном положении как сумму кинетических энергий тел, входящих в её состав. На расчётной схеме показать все кинематические характеристики, от которых зависит кинетическая энергия системы.

5.Выразить кинетическую энергию системы через скорость тела, перемещение которого задано. ДИ

114

6. Изобразить на расчётной схеме все внешние и внутренние силы системы (в случае неизменяемой механической системы – только внешние силы).

7. Вычислить сумму работ сил, приложенных к системе, на заданном её перемещении.

Перемещения точек приложения сил и углы поворота тел, к которым

Сопредел ть скомую скорость, приравняв полученные в пунктах 5, 6 выражен я к нет ческой энергии системы и суммы работ сил.

приложены моменты, выразить через перемещение тела, которое задано.

8. Из теоремы об изменении кинетической энергии в конечной форме

15.3. Контрольные вопросы для тестирования студентов

1. Что называется к нетической энергией материальной точки?

К нет ческой энергией материальной точки называют половину веден я массы точки на квадрат ее скорости:

	mV 2			mV 2
произ
T =		;	T =		.
	2			2
Квадрат модуля скорости равен скалярному квадрату вектора
скорости, поэтому данные выражения равноценные. Кинетическая энергия
б
является скалярной положительной величиной. В СИ единицей
кинетической энергии является джоуль: 1				ж=1 Н·м.

2. Что называется кинетической энергией механической системы?
Кинетической энергией механической системы Т называют сумму
кинетических энергийАвсех точек механической системы, т.е.
n m V 2		n m V 2
T = ∑	k k	= ∑	k k	.
	2		2
k =1		k =1
Кинетическая энергия как точки, так и системы не зависит от
направления скоростей точек. Кинетическая энергия может быть равна
	Д
нулю для системы только при условии, если все точки системы находятся
в покое.			И

3. Сформулируйте теорему Кёнига.

Теорема Кенига: кинетическая энергия системы в абсолютном

движении складывается из кинетической энергии центра масс, если в нем сосредоточить всю массу системы, и кинетической энергии системы относительно центра масс, т.е.

	mV	2			m V 2
T =	c		+Tc(r) , где	Tc(r) = ∑	k kr .

	2				2

115

Величина Tc(r) является кинетической энергией относительного

движения системы относительно системы координат, движущейся поступательно вместе с ее центром масс, или кинетической энергией системы относительно центра масс.

4. Запишите формулу для вычисления кинетической энергии твердого тела

при поступательном движении.

При поступательном движении твердого тела скорости всех точек

тела од наковы: Vk

=V ,

поэтому кинетическая энергия тела равна сумме

кинетическ

х энерг

й всех его точек, т.е.

при

СT = ∑

mkVk

= V

∑m

= mV

k =1 2

k =1 k

где m – масса тела; V – скорость точки тела.

5. Зап ш те формулу для вычисления кинетической энергии твердого тела

вращательном дв жен и.

= J z

T = ∑ mkVk =

∑mk hk2 =

J z

или

k =1 2

k =1

где J – момент инерции тела относительно оси вращения Oz.

Кинетическая энергия тела при вращательном движении вокруг неподвижной оси равна половине произведения момента инерции тела

относительно оси вращения на квадрат угловой скорости тела.
					Д
6. Запишите формулу для вычисления кинетической энергии твердого тела
при плоскопараллельном движении.
Плоское движение тела по теореме Кенига
можно рассматривать как совокупность двух
движений:	поступательного				переносного
					И
движения вместе с центром масс и
относительного		вращательного			движения
относительно центра масс.
Следовательно,			по теореме Кенига
кинетическая энергия при плоскопараллельном
движении равна
			mV 2	ω2
		T =	2c + Jcz	2 .

При плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела вместе с

116

Fτ=Fсоsφ,

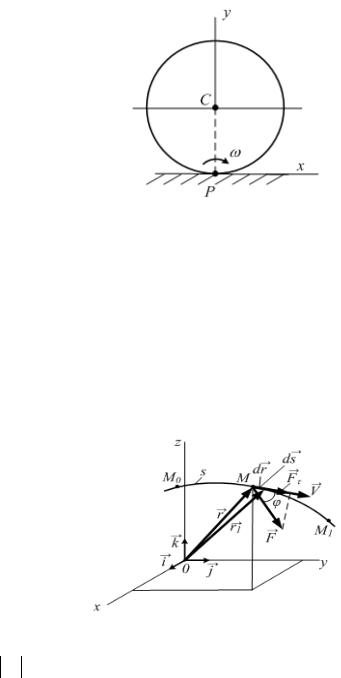
центром масс и кинетической энергии от
вращения вокруг оси, проходящей через центр
масс и перпендикулярной плоскости движения.
Учитывая, что VC=ω·CP (P– мгновенный
центр скоростей), получаем второй способ
определения	кинетической энергии					твердого
С
тела при плоском движении
T =	ω2			2 ) = J pz		ω2	,
	2					2
кинетич
где J pz – момент			нерц и тела относительно оси Рz,					проходящей через
мгновенный центр скоростей перпендикулярно плоскости движения.
К нет ческая			энергия		тела	при плоском		движении равна
еской энерг			этого тела при вращении относительно МЦС.
б
Плоское дв жен е, состоящее из двух движений (поступательного и
вращательного), можно заменять одним вращением вокруг мгновенного
центра скоростей.
7. Зап ш те формулу для вычисления элементарной работы силы для
			А
случая, когда движение точки приложения силы задано векторным способом.
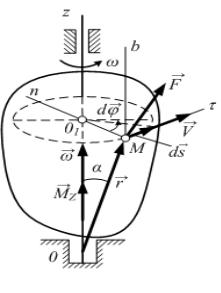
Элементарная ра ота d					силы	F	на
элементарном		перемещении			ds	равна
произведению	касательной составляющей
силы на элементарное перемещение, т.е.
		dA = Fτds ,			Д

где Fτ – проекция силы F на направление

скорости точки приложения или на направление элементарного перемещения.

Элементарное перемещение ds по модулюИсовпадает с элементарным изменением радиуса-вектора ds = dr , тогда

где φ – угол между вектором силы и вектором скорости точки М.

8. Выясните, при каких условиях элементарная работа силы положительна,

отрицательна, равна нулю.

Элементарная работа равна произведению модуля силы, модуля перемещения силы и косинуса угла между векторами силы и перемещения.

dA=Fdscosφ.

117

Элементарная работа является скалярной величиной. Ее знак определяется знаком проекции силы Fτ на положительное перемещение ds.

При Fτ >0 элементарная работа dA>0, а при Fτ < 0 dA<0.

Отметим частные случаи: если φ = 0°, то dA=Fds; если φ = 90°, то dA =0; если φ =180°, то dA= –Fds.

Таким образом, если сила перпендикулярна элементарному перемещению, то ее элементарная работа равна нулю. В частности, работа нормальной составляющей силы Fn всегда равна нулю.

9. Зап ш те формулы для вычисления работы силы на конечном перемещен .

Тогда работу А можно выразить формулой

С			n
С			A = lim Σ dAk ,
			n→∞ k=1
где dAk – работа на k-м элементарном перемещении. Так как сумма в
формуле		является интегральной		суммой определения
криволнейного нтеграла на участке кривой М0 M1 , то заменим ее
интегралом
			M1
			A = ∫Fτds .
			M0
	работы
		А
Используя другие выражения для элементарной работы, полную
работу силы на конечном перемещении М0М можно представить в разных
формах:	M1	M1	Д
	M1	M1			t
	A = ∫Fdr	= ∫(Fxdx + Fydy + Fz dz) или		A = ∫FVdt ,
	M0	M0			0
где момент времени t = 0 соответствует точке М0, а мо мент времени t –
точке M1 .			И
точке M1 .

10. Как вычисляется работа силы тяжести?

Работа силы тяжести равна произведению силы на величину вертикального перемещения и имеет положительное или отрицательное значение:

A=±Gh.

Величина работы силы тяжести положительная, когда векторы силы

тяжести G и вертикального перемещения h совпадают, т.е. работа положительная при опускании точки и отрицательная при подъеме. Работа силы тяжести на замкнутой траектории равна нулю.

118

11. Как вычисляется работа силы

упругости?

Работа силы F на конечном перемещении M H M К равна

хк		cx	2	xК		2		2

А=−с ∫	xdx = −					сxK	−	сxH	.
		2			= −	2		2

хн				xH

Работа растяжен я пружины отрицательна. Если пружина будет
возвращать накопленную энергию, ее работа будет положительна, она
гидравлОна также равна нулю, если точки M H и M К	перемещаются по
может спользоваться для совершения полезной работы.
СНа этом пр нц пе работают пружинные,	пневматические и
ческ е аккумуляторы энергии.
Работа л нейной силы упругости не зависит от траектории
б

перемещен я, ра ота по лю ому замкнутому циклу равна нулю.

сфере, в центре которой закреплена пружина.

12. Как выч сляется ра ота силы трения?

Вектор силы трения является касательным к траектории движения и направлен противоположно вектору скорости точки М приложения силы.

Точка	М	перемещается	по
шероховатой		поверхности	по
криволинейной траектории.			Д
Сила трения определяется по закону
Кулона:		А
	FTP = fN .
Работа силы трения на конечном перемещении М0М1 определяется по
формуле				И
		M1	M1	И
		M1	M1	fNds .
		A =– ∫FTP ds = − ∫		fNds .
		M0	M0

Если N =const , то FTP = const и A = −FTP s ,

где s – длина дуги М0М1, по которой перемещается точка М.

13. Что называется мощностью силы?

Мощность силы или интенсивность какого-либо источника силы можно оценивать работой, которую он может совершить за единицу

времени. Мощность N = dA .

Мощность можно представить в виде N = F V = FV cosϕ.

119

Таким образом, мощность равна скалярному произведению векторов силы и скорости точки. Из формулы следует, что чем больше скорость, тем

меньше сила при одной и той же мощности. Есл и N = FV = const , то при изменении силы необходимо менять скорость. Следовательно, если от источника силы с заданной мощностью нужно получить большую силу, то её можно получить только при малой скорости. В СИ единицей мощности является ватт: 1 Вт = 1 Дж/с.

14. Как определяется работа силы,
приложенной к твердому телу, вращающемуся
вокруг неподв жной оси?
Элементарная					работа		силы,
приложенной к какой-либо точке тела,
С
вращающегося вокруг неподвижной оси,
равна	про зведен ю				момента		силы
	тельно		оси		вращения			на
элементарный угол поворота тела.
Полная			ра ота		на	конечном
относи
перемещен			ϕ
			ϕ
			A = ∫	M zdϕ.
			0
		б
В частном случае, если момент силы относительно оси вращения
является постоянным, т. е. M z (F) = const, работу определяют по формуле
					A = ± M zϕ,
где φ –	угол поворота тела.
				А
Работа положительна, если направление момента совпадает с
направлением вращения тела.

15. Как определяется мощность силы, приложенной к твердому телу, вращающемуся вокруг неподвижной оси?

Мощность в случае вращения твердого тела вокруг неподвижной оси
определяется по выражению	Д
N = dA =	M z dϕ	= ±M zω.
	dt
dt
Мощность силы, приложенной к телу, вращающемуся вокруг
неподвижной оси, равна произведению момента силы относительно оси
		И

вращения тела на угловую скорость. Знак мощности определяется аналогично знаку работы.

16. Сформулируйте теорему об изменении кинетической энергии материальной точки в дифференциальной форме.

120

Теорема об изменении кинетической энергии для точки в дифференциальной форме: дифференциал кинетической энергии точки равен элементарной работе силы, действующей на точку:

		mV 2
		d			= dA.
			2
			2
17.	формулируйте	теорему			об	изменении			кинетической	энергии
материальной точки в конечной форме.
Теорему об зменен и кинетической энергии точки в конечной форме
		mV 2	–		mV	2
изменен			–		0 = A,
изменен					2
		2			2
Ст. . к нет ческой энергии точки на каком-либо перемещении
равно работе с лы, действующей на точку на том же перемещении.
18.	формул руйте	теорему			об	изменении			кинетической	энергии
	об
механической с стемы в д фференциальной форме.
Теорема		и кинетической энергии механической системы в
дифференц альной форме
		dT			= N e + N i .
	А
		dt
Производная по времени от кинетической энергии механической
системы равна сумме мощностей внешних и внутренних сил системы.
19. Сформулируйте теорему об изменении кинетической энергии
механической системы в конечной форме.
		T −T	=		Ae	+ Ai	.
		0			1−2	1−2
Изменение кинетической энергии механической системы при ее
перемещении из одного положения в другое равно сумме работ внешних и
внутренних сил на этом же перемещении.								И
								И
20. Влияют ли внутренние силы механической системы на изменение ее
кинетической энергии?				Д
Если система содержит недеформируемые абсолютно твердые тела, то
						n			= 0 .
работа внутренних сил системы равна нулю: ∑Aki									= 0 .
						k =1

21. Дайте определение понятию «силовое поле».

Пусть точка движется в некотором пространстве и на нее со стороны пространства действует сила, которая зависит от положения точки в этом пространстве, но не зависит от скорости движения. В этом случае говорят, что в пространстве задано силовое поле или что точка движется в силовом поле. Соответствующие понятия для системы материальных точек аналогичны.

121

Силы, зависящие от положения точек их приложения, в механике встречаются часто. Например, сила упругости, приложенная к материальной точке, которая движется по горизонтальной прямой под действием пружины. Важнейшим примером силового поля в природе является гравитационное поле: действие Солнца на планету данной массы определяется в каждой точке пространства законом всемирного тяготения.

22. Какое силовое поле называется потенциальным?

иловое поле называют потенциальным, если существует скалярная

функц я U,

зав сящая только от координат xk , yk , zk точки Мк – точки

материальной с стемы:

F =

∂U (x, y, z)

;

∂U (x, y, z) ; F

= ∂U (x, y, z) ,

k =1,2,...,n.

Сkx

∂zk

∂xk

∂yk

Функц я U(x, y, z) называется силовой функцией.

23.

Расскаж те

свойствах

силовой

функции

силовой

Рассмотр м

свойства

функц .

Элементарная

ра ота

связана с

силовой функцией следующим о разом:

dA = F dx + F

dy + F dz =

∂U

dx +

∂U

dy +

∂U

dz = dU ,

т.е. dA = dU .

∂x

∂y

∂z

Таким образом, элементарная работа силы в потенциальном силовом

поле равна полному дифференциалу от силовой функции.

Полная работа силы

на участке от точки M0 (x0 , y0 , z0 ) до точки

M1 (x1 , y1 , z1 ) равна

A =

∑dA =

∑dU =U1(x1, y1, z1) −U0 (x0 , y0 , z0 ) =U1 −U0 ,

где A =U1 −U0 .

Из полученных выражений следуют выводыИ:

1. Работа силы в потенциальном силовом поле по замкнутой траектории равна нулю.

2. Работа силы в поте нциальном силовом поле зависит только от начального и конечного положений точек и не зависит от формы траектории.

24. Покажите связь потенциальной силы с энергией?

Потенциальной энергией П в рассматриваемой точке силового поля М называют работу, которую совершают силы поля, действующие на

122

материальную точку при ее перемещении из данного положения М в начальное положение М0, т.е.

П = AMM0 или П = AMM0 =U0 – U .

вяжем силовую функцию U с потенциальной энергией. Имеем

F =

∂U

= –

∂П

; F =

∂U

= −

∂П

;

F =

∂U

= −

∂П

∂x

y ∂y

∂y

z ∂z

∂z

∂x

т.е. dA = dU = −d

;

A =U −U0 = П0 − ПП, или

П = −U .

25. Пр вед те пр меры вычисления потенциальной энергии.

1. Однородное поле тяжести. Пусть m – масса точки; g – ускорение свободного паден я.

Тогда по формуле A = mgh получим

= 0;

Fy = 0; Fz = −mg;

П = A = −mgz.

ловое

поле

упругой

пружины.

Пусть

материальная точка

движется вдоль

оси Оx под действием

пружины, к которой она

лена.

прикре

xК

хк

По формуле А=−с ∫ xdx = −

сxK

−

сxH

= −

хн

если при х=0 пружина не деформирована, то, полагая х0=0, получим

П = −A =

1 cx2 .

26. В чем заключается закон сохранения механической энергии?

Для механическойАсистемы имеем dT = dA + dA ,

т.е. приращение кинетической энергии системы за конечное время равно

работе всех сил системы за то же время.

Пусть все силы системы (внутренние и внешние) потенциальны и их

потенциал П не зависит явно от времени. В этом случае элементарная

работа сил системы будет полнымДдифференциалом dA + dA = −dП ,

тогда следует, что dT + dП = 0 .

Сумма кинетической и потенциальной

энергий

называется

полной

механической

энергией

системы:

E =T + П = const . И

Равенство называется интегралом движения, т.е. если все силы системы потенциальны и потенциал не зависит от времени, то при движении системы ее полная механическая энергия постоянна. Это закон сохранения механической энергии. Следует иметь в виду, что для справедливости закона сохранения механической энергии требование о том, чтобы все силы системы были потенциальными, необязательно. Достаточно потребовать, чтобы потенциальными были силы, работа которых на действительном перемещении системы отлична от нуля.

123

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2016 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20213.84 Mб72187.pdf
#
07.01.20213.85 Mб12188.pdf
#
07.01.20213.85 Mб162189.pdf
#
07.01.2021356.57 Кб0219.pdf
#
07.01.20213.86 Mб112190.pdf
#
07.01.20213.86 Mб152191.pdf
#
07.01.20213.87 Mб72192.pdf
#
07.01.20213.88 Mб22193.pdf
#
07.01.20213.89 Mб202194.pdf
#
07.01.20213.91 Mб82195.pdf
#
07.01.20213.92 Mб12196.pdf