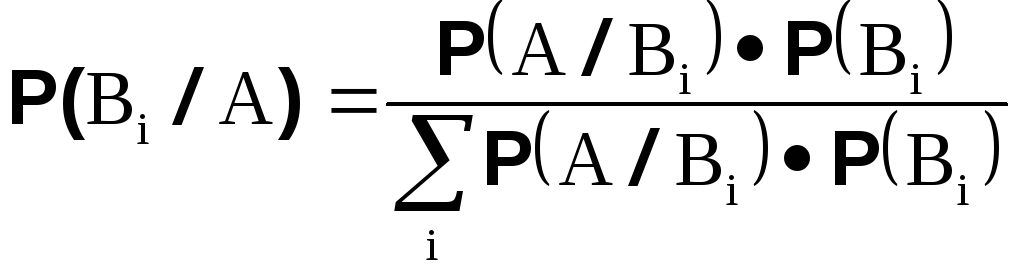- •Теория вероятностей Введение в теорию вероятностей Предмет теории вероятностей
- •Возникновение и развитие теории вероятностей До появления аксиоматики Колмогорова
- •В наше время
- •Необходимость теории вероятностей как науки
- •Возможность анализа случайных явлений
- •Расчет шансов и прогнозирование последствий
- •Игра по крупному
- •Основные понятия и определения Первичные понятия Опыт (эксперимент)
- •Элементарный исход
- •Пространство элементарных исходов
- •Советы по построению пространства элементарных исходов.
- •Определения Подмножества
- •Операции над подмножествами
- •Случайные события
- •Информационный смысл понятия сигма - алгебра
- •Пересечение сигма-алгебр
- •Вероятностное пространство
- •Парадокс определения вероятностного пространства
- •Независимые события
- •Теорема (о непрерывности вероятностной меры)
- •Дискретная вероятностная модель
- •Конечное пространство элементарных исходов
- •Классическая вероятностная модель
- •Связь классической вероятностной модели с комбинаторикой
- •Основная формула комбинаторики
- •Факториал
- •Урновая схема
- •Общее определение вероятности для экспериментов с конечным или счетным числом исходов
- •Дискретное распределение и вероятность
- •Равномерное распределение - классическая вероятностная модель
- •Биномиальное распределение – схема Бернулли
- •Мультиномиальное распределение – схема бросания частиц по ячейкам
- •Геометрическое распределение – испытания до первого успеха
- •Распределение Паскаля – испытания до m-того успеха
- •Пуассоновское распределение - теорема Пуассона
- •Теорема Пуассона.
- •Сходимость по вариации - приближение одних моделей другими
- •Использование понятия независимости для построения моделей. Произведение вероятностных пространств.
- •Примеры построения моделей.
- •Расчет надежности при параллельном соединении элементов.
- •Расчет надежности при последовательном соединении элементов
- •Расчет надежности сложной системы.
- •Замечания к примерам.
- •Условная вероятность
- •Урновая схема
- •Марковская зависимость
- •Формула полной вероятности и формула Байеса
- •Случайные величины
- •Отображения вероятностных пространств
- •Случайная величина
- •Борелевская сигма-алгебра
- •Свойства случайных величин
- •Случайный вектор
- •Распределения случайных величин и векторов
- •Точки непрерывности и разрыва функции распределения
- •Несобственные функции распределения
- •Геометрическое распределение
- •Мера Лебега на прямой.
- •Плотность распределения
- •Вероятностный смысл плотности распределения
- •Бета-распределение на отрезке [0,1]
- •Смеси распределений.
- •Нормальное (гауссовское) распределение.
- •Экспоненциальное (показательное) распределение.
- •Гамма-распределение.
- •Построение меры в конечномерном пространстве Борелевская сигма-алгебра в конечномерном пространстве
- •Определение случайного вектора
- •Мера Лебега в конечномерном пространстве
- •Мера Лебега на квадрате - Задача о встрече
- •Независимые случайные величины
- •Многомерное нормальное распределение
- •Числовые характеристики случайных величин и векторов
- •Интеграл Лебега – математическое ожидание
- •Свойства интеграла Лебега (математического ожидания)
- •Теоремы о предельном переходе под знаком интеграла Лебега
- •Теорема Лебега о мажорируемой сходимости
- •Неравенства Неравенство Маркова
- •Неравенство Чебышева. Дисперсия
- •Неравенство Коши-Буняковского-Шварца. Ковариация
- •Неравенство Йенсена.Выпуклые функции
- •Неравенство Ляпунова.Моменты
- •Вычисление математического ожидания.
- •Теорема Лебега о замене переменных
- •Вычисление интеграла Лебега на прямой.
- •Вычисление интеграла Лебега в произведении пространств. Теорема Фубини
- •Теорема Фубини
- •Вычисление маргинальных плотностей
- •Вычисление числовых характеристик важных распределений.
- •Абсолютная непрерывность вероятностных мер
- •Абсолютно непрерывные и сингулярные меры и распределения
- •Теорема Радона-Никодима
- •Суммирование независимых случайных величин
- •Сходимость последовательностей случайных величин и их распределений
- •Сходимость почти наверное
- •Закон больших чисел в форме Бернулли
- •Теорема Шеффе
- •Преобразование Лапласа и производящая функция
- •Теорема единственности для характеристических функций и характеристические функции важных распределений
- •Предельные теоремы теории вероятностей
- •Классическая схема
- •Закон больших чисел в форме Чебышева
- •Закон больших чисел для схемы серий
- •Закон больших чисел в форме Хинчина
- •Условное математическое ожидание, условная вероятность и условное распределение
- •Определение и основные свойства условного математического ожидания
- •Теорема существования и единственности условного математического ожидания
- •Математическое ожидание одной случайной величины относительно другой
- •Свойства условного математического ожидания
- •Определение условной вероятности, условного распределения и условной плотности Условная вероятность
- •Условное распределение
- •Вычисление условной плотности и условного математического ожидания
Парадокс определения вероятностного пространства
Вернемся к исходной постановке задачи теории вероятностей. Нашей целью было построение математической модели случайного явления, которая помогла бы количественно оценить вероятности случайных событий. В то же время для построения вероятностного пространства необходимо задать вероятность, т.е. вроде бы именно то, что мы ищем (?).
Разрешение этого парадокса в том, что для полного определения вероятности как функции на всех элементах F, обычно достаточно задать ее на лишь на некоторых событиях изF,вероятность которых нам легко определить,а затем, пользуясь ее счетной аддитивностью, вычислить на любом элементеF.
Независимые события
Важным понятием теории вероятностей является независимость.
События AиBназываются независимыми, если
![]()
т.е. вероятность одновременного осуществления этих событий равна произведению их вероятностей.
Попарно
События в счетном или конечном наборе называются независимыми попарно, если любая пара из них является парой независимых событий
![]()
В совокупности
События в счетном или конечном наборе называются независимыми в совокупности , если вероятность одновременного осуществления любого конечного поднабора из них равна произведению вероятностей событий этого поднабора.
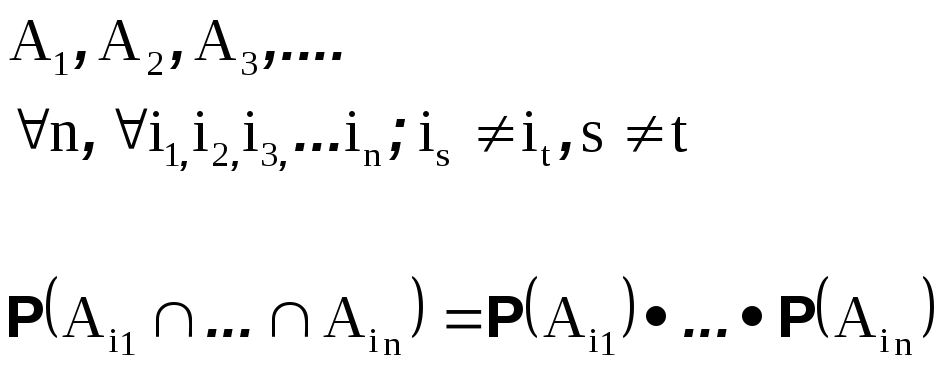
Ясно, что независимые в совокупности события независимы и попарно. Обратное неверно.
Условная вероятность
Условной вероятностью события Aпри условии, что произошло событиеB называется величина
![]()
Условную вероятность пока определим лишь для событий B, вероятность которых не равна нулю.
Если события AиBнезависимы, то
![]()
Свойства и теоремы
Простейшие свойства вероятности
|
Следует из того, что А и не-А противоположны и свойства конечной аддитивности вероятности |
Вероятность противоположного события |
|
Следует из того, что невозможное и достоверное события противоположны |
Вероятность невозможного события
|
|
Следует из того , что
|
Монотонность вероятности
и в этом случае
|
|
Следует из того, что любое событие содержится в пространстве элементарных исходов |
Ограниченность вероятности
|
|
Следует из представления |
Вероятность объединения событий
|
|
Следует из предыдущего |
Полуаддитивность вероятности
|
|
Докажите сами! |
Счетная полуаддитивность вероятности
|
|
Следует из счетной аддитивности вероятности и определения полной группы событий |
Вероятности полной группы событий Сумма вероятностей полной группы событий равна 1.
|
|
Следует из счетной аддитивности вероятности, определения полной группы событий и определения условной вероятности |
Формула полной вероятности
Если
Если вероятности всех событий полной группы больше нуля, то также
|
|
Следует из предудущей формулы и определения условной вероятности |
Формула Байеса
Если
|
Теорема (о непрерывности вероятностной меры)
Формулировка.
Пусть
![]()
убывающая последовательность событий с пустым общим пересечением
![]()
Тогда
![]() .
.
Доказательство.
Заметим, что события
![]()
попарно несовместны и
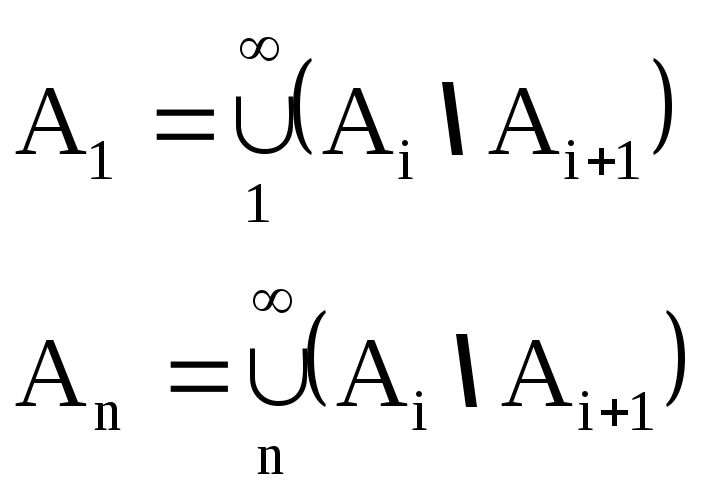
Следовательно ряд из вероятностей событий
![]()
сходится и его хвост, равный
![]()
стремится к нулю.
|
Докажите! |
Верно и обратное – ограниченная непрерывная конечно-аддитивная функция является счетно-аддитивной. |
Заметим,
что для доказательства важна только
конечность значения
![]() ,
поэтому теорема справедлива не только
для вероятностных, но и для любых
конечнных мер.
,
поэтому теорема справедлива не только
для вероятностных, но и для любых
конечнных мер.