Темы лекций Функциональный анализ

Лекция №1

1. Множества, операции над множествами. Формулы двойственности.

2. Биекция: [a,b]↔ [a₁ ,b₁]; (a,b)↔ (a₁ ,b₁); (-π/2, π/2)↔ (-∞;∞); N↔2N.

3. Эквивалентные множества; мощность множества; сравнение мощностей.

4. Счетные множества. Счетность Z.

5. Утверждения: любое бесконечное множество содержит счетное подмножество; любое подмножество счетного множества конечно или счетно.

6. Теорема: а) объединение конечного и счетного множества счетно; б) объединение конечного числа счетных множеств счетно; г) объединение счетного числа счетных множеств счетно (.

7. Пример: мн-во Q (разобран на семинаре).

8. Теорема: если А – бесконечно, а В – конечно или счетно, то 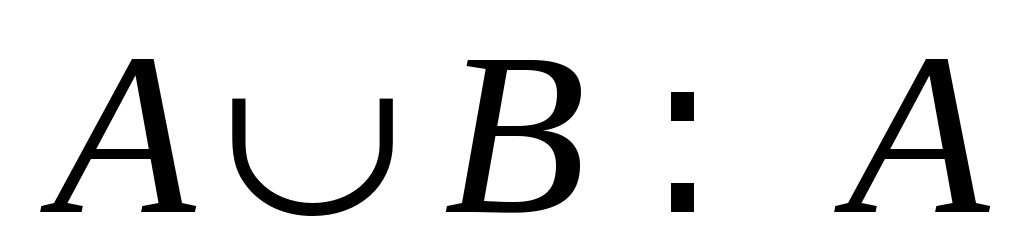(доказана на семинаре). Следствие: А – бесконечное несчетное, а В – конечное или счетное его подмножество, тогда ().

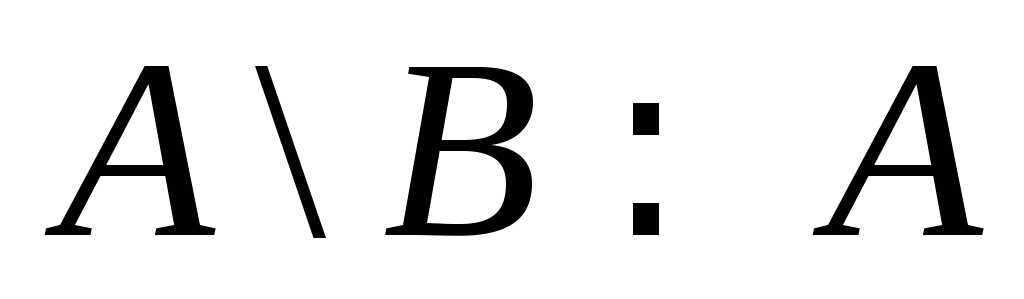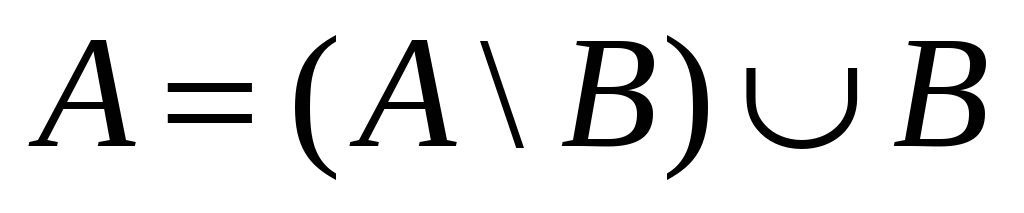9. Пример: [0,1]↔ [0,1) ↔ (0,1) ↔ R¹.

Лекция №2

1. Прямое произведение двух счетных множеств счетно (таблица T(n,m)).

2. Пример: мн-во точек в Rⁿ c рациональными координатами счетно:

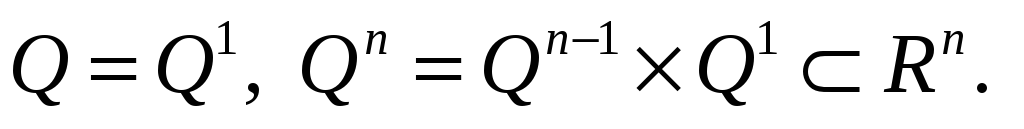
3. Теорема: если элементы множества А определяются n значками, каждый из которых независимо от других пробегает счетное множество, то мн-во А счетно (док-во по индукции). (Предыдущий пример можно решить на основании этой теоремы.)

4. Примеры: мно-во многочленов с рациональными коэффициентами счетно; мн-во алгебраических чисел счетно.

5. Теорема: множество точек отрезка [0,1] несчетно (доказана на семинаре). Мощность континуум.

6. Примеры: мн-во двоичных последовательностей ↔ [0,1); мн-во возрастающих последовательностей натуральных чисел; мн-во последовательностей натуральных чисел (было на семинаре).

7. Теорема: конечное или счетное объединение непересекающихся множеств мощности с (континуум) также имеет мощность с (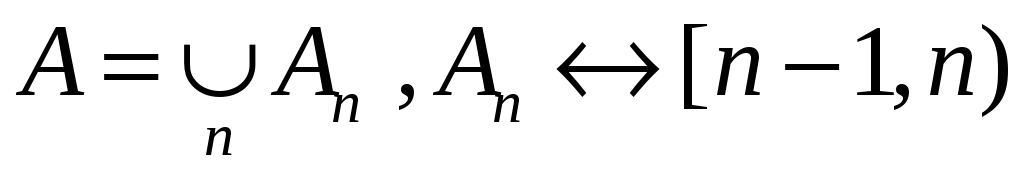). (То же верно для континуального объединения.)

8. Пример: мн-во всех многочленов с вещественными коэффициентами любых степеней ( А_n – мн-во многочленов не выше n- ой степени).

9. Теорема. Если элементы множества А определяются n значками (cчетным числом значков), каждый из которых независимо от других пробегает множество мощности с, то мн-во А имеет мощность с:

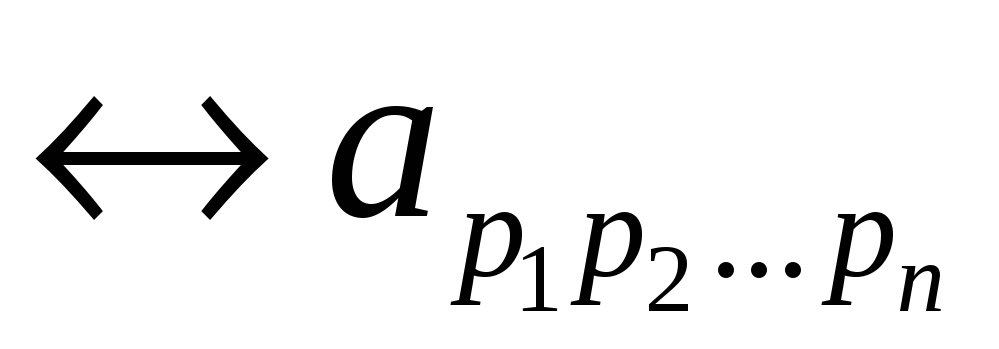
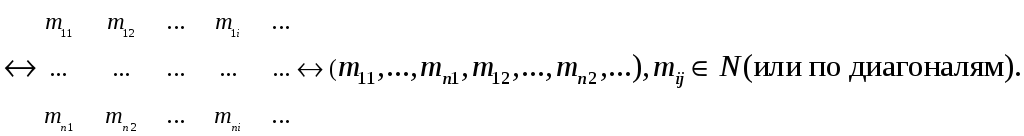
10. Пример. Континуальность: множества Rⁿ; множества R^∞ всех последовательностей действительных чисел.

11. Теорема: если элементы множества А определяются cчетным числом значков, каждый из которых независимо от других принимает два значения, то мн-во А имеет мощность с. (Рассмотреть сначала последовательности из нулей и единиц и сопоставить их с двоичными числами из [0,1].)

12. Теорема Кантора-Бернштейна (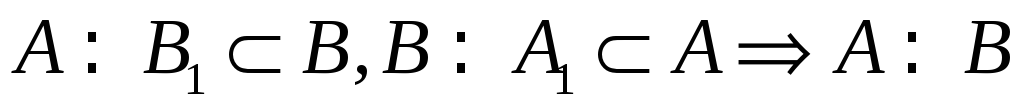) и следствие из нее (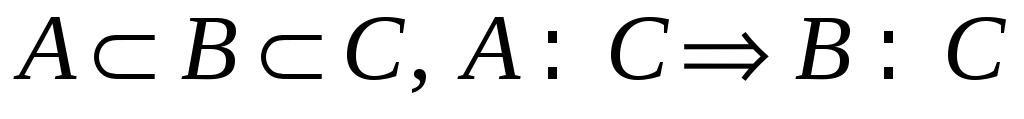). Континуальность множества всех непрерывных функций на отрезке.

13. Теорема: множество всех подмножеств данного множества имеет мощность большую, чем исходное множество.

Лекция №3

1. Метрические пространства. Открытый и замкнутый шары, окрестность, открытое и замкнутое множества, предел последовательности.

2. Открытый шар – открытое множество. Замкнутый шар – замкнутое множество.

3. Теоремы: а); 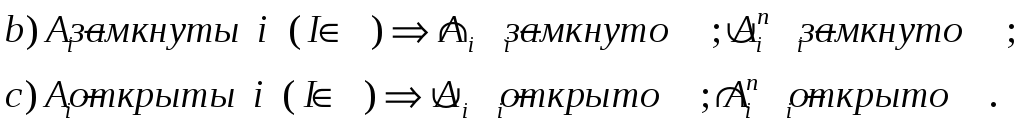Замечание к теоремам b), c) (нельзя заменить n на бесконечность)

4. Примеры: Rⁿ, С[a,b], C₂[a,b], l₁, l₂, l_∞.

5. Нормированные пространства (примеры). Метрика, порожденная нормой.

6. Сходимости по норме и покоординатная (l₁, l₂, l_∞) , по норме и поточечная (С[a,b], C₂[a,b]).

7. Предгильбертовы пространства. Норма, порожденная скалярным произведением. Примеры: C₂[a,b], l₂.

8. Тождество параллелограмма. Примеры не предгильбертовых пространств: С[a,b], l₁ ,l_∞.

9. Полные пространства. Примеры полных (Rⁿ, С[a,b], l₂) и неполных (C₂[a,b]) пространств.

10. Замыкание [A] множества A. Плотные и всюду плотные множества. Примеры всюду плотных множеств: [Q]=R; [P_n(x)]=C[a,b] , C₂[a,b]; [финитные последовательности]=l₂, l₁ ,l_∞.

11. Сепарабельные пространства. Примеры: [P_n(x) с рациональными коэффициентами)]=C[a,b] , C₂[a,b]; [финитные последовательности с рациональными координатами]=l₂, l₁ ; несепарабельные –BC(R), l_∞.

12. Банаховы (Rⁿ, C[a,b], l₂,l₁ ,l_∞) и гильбертовы (l₂) пространства.

13. Эквивалентные нормы. Теорема: любое конечномерное ЛНП является полным и сепарабельным. Пополнение метрического пространства.

14. Непрерывные отображения. Теорема: прообраз открытого(замкнутого) множества открыт(замкнут).

15. Сжимающие отображения. Теорема о сжимающем отображении. Оценка погрешности.

Литература. 1) Натансон И.П. Теория функций вещественной переменной.

2) Колмогоров А.Н., С.В.Фомин. Элементы теории функций и функционального анализа.

3