Использование понятия независимости для построения моделей. Произведение вероятностных пространств.

Во многих практических задачах априори ясно, что некоторые случайные события в эксперименте независимы. Естественно требовать, чтобы эти же события были независимы и в математической модели, описывающей данный эксперимент. Определение независимости в теории вероятностей имеет аналитический характер и, следовательно, требование независимости событий в модели, приводит к ограничениям на используемую вероятность. Эти ограничения вместе с дополнительными качественными (симметричность) или количественными требованиями часто позволяют однозначно определить подходящую вероятность.

Рассмотрим, например, эксперимент, описываемый элементарным исходом вида

где первая координата описывает одну случайную компоненту, а вторая другую случайную компоненту опыта.

Если предположить N₁вариантов у первой компоненты и N₂– у второй, то для того, чтобы задать вероятность, необходимо в общем случае N_1*N₂ –1 вероятностей элементарных исходов (столько, сколько всего пар минус одна – мы знаем , что сумма всех вероятностей пар должна быть равна 1).

Если заранее известно, что компоненты независимы, то количество вероятностей событий, которые мы должны задать , чтобы однозначно определить вероятность, уменьшается до N₁ +N₂ –2 (N₁ –1 на первую и N₂ –1 на вторую компоненту). Далее, вероятность элементарного исхода определяется как произведение вероятностей значений его компонент.

Подобный прием мы использовали при построении моделей для схемы Бернулли и мультиномиальной схемы.

В общем случае пусть элементарный исход некоторого эксперимента представляется в виде вектора с n координатами.

Пусть известно, что координаты вектора описывают независимые компоненты, т.е. все события вида

должны быть независимы. Тогда, если для описания i-той компоненты использовать вероятностное пространство

с соответствующими распределениями

то для описания всего эксперимента естественно использовать следующее вероятностное пространство

где

т.е.

т.е.

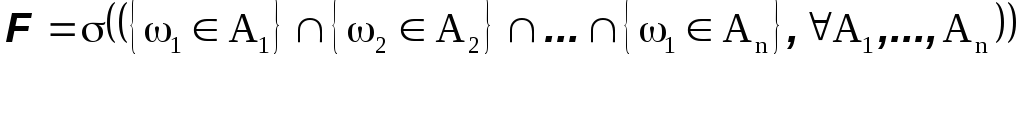
минимальная сигма-алгебра, содержащая все события, описывающие поведение компонент.

Распределение в результирующем пространстве определяется по формуле

Так построенное вероятностное пространство называется произведением вероятностных пространств

а его составляющие, соответственно, произведениями пространств элементарных исходов, произведением сигма-алгебр и произведением вероятностных мер.

Примеры построения моделей.

Ранее были рассмотрены два примера построения моделей с использованием понятия независимости – схема Бернулли и мультиномиальная схема. Приведем еще несколько примеров.

Расчет надежности при параллельном соединении элементов.

Для повышения надежности ответственной системы обычно применяют резервирование ее элементов, т.е. дублируют важные части системы. Вместо одного элемента включают одновременно несколько элементов для того, чтобы при отказе одного из них система на прекращала работу.

Предположим, что вероятность отказа основного элемента (за некоторый промежуток времени – период работы) равна 0,1. Нас интересует надежность системы, составленной из параллельно подключенных 4 одинаковых элементов. Если предположить, что отказы элементов вызываются внутренними (брак при изготовлении, усталость материала, износ и т.п.), а не внешними (повышение напряжения питания, физическое разрушение при аварии) причинами, то естественно ( в первом приближении) считать отказы разных элементов независимыми.

В качестве элементарного исхода рассмотрим двоичный вектор

имеющий 4 координаты – соответственно состоянию каждого элемента в конце заданного промежутка времени ( 1 – исправен, 0 - отказ). Из условия задачи следует, что события , связанные с разными координатами должны быть независимы, следовательно, используя формулу

в нашем случае получаем

и т.д.

Система будет работоспособной весь период времени, если не отказал хотя бы один из ее элементов. Этому условию удовлетворяют все элементарные исходы, кроме одного

Сообразите, как рассчитать надежность такой системы при неодинаково надежных, но независимых элементах	Таким образом, вероятность отказа всей системы равна а вероятность безотказной работы (надежность)
Покажите ,что это действительно можно делать, если отказы элементов независимы в совокупности	Заметим, что если рассматриваемая система является частью более сложной системы, то можно при расчетах надежности заменить эти четыре элемента одним, с вероятностью отказа 0,0001.