Мера Лебега на прямой.

Можно показать, что существует (не вероятностная) мера на прямой, которая приписывает каждому отрезку его длину. Эта мера называется мера Лебега (на прямой). В дальнейшем будем обозначать эту меру

Плотность распределения

В тех случаях, когда функцию распределения можно представить в виде интеграла (Римана) от неотрицательной функции

функцию f называют плотностью, соответствующей функции распределения F, или плотностью F .

Если функция распределения имеет плотность, то эта функция распределения непрерывна и такие функции распределения называют абсолютно непрерывными. Точные смысл понятию абсолютная непрерывность будет дан в дальнейшем. Заметим, что представление функции распределения в виде интеграла от некоторой функции неоднозначно, поэтому у одной функции распределения может быть несколько различных плотностей. Впрочем, различаться они могут только в не очень большом числе точек. Поэтому обычно плотностью называют наиболее прилично ведущую себя функцию f – непрерывную или почти непрерывную. Ее и приводят в различных справочниках. Нарисуем, например, график плотности равномерного на отрезке [0,2] распределения.

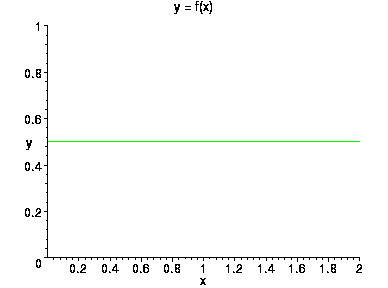
Очевидно, любая плотность удовлетворяет условию

Зная плотность распределения нетрудно подсчитывать вероятности различных множеств.

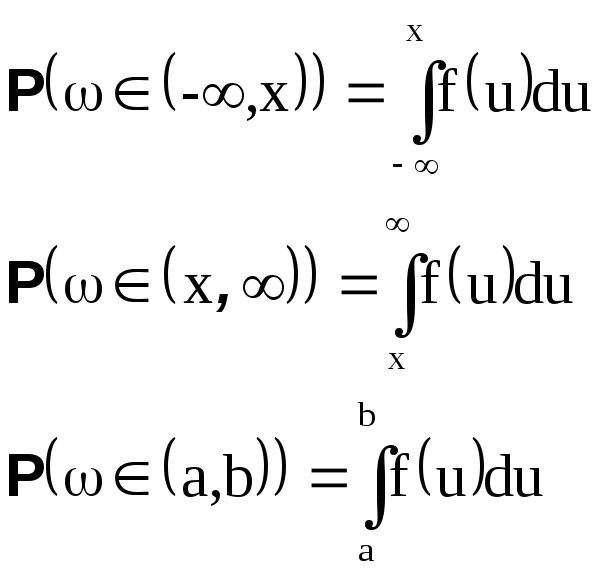
и, вообще, если индикаторная функция

множества

интегрируема по Риману на любом конечном отрезке, то

Если g(x) – неотрицательная функция, удовлетворяющая условию

то функция

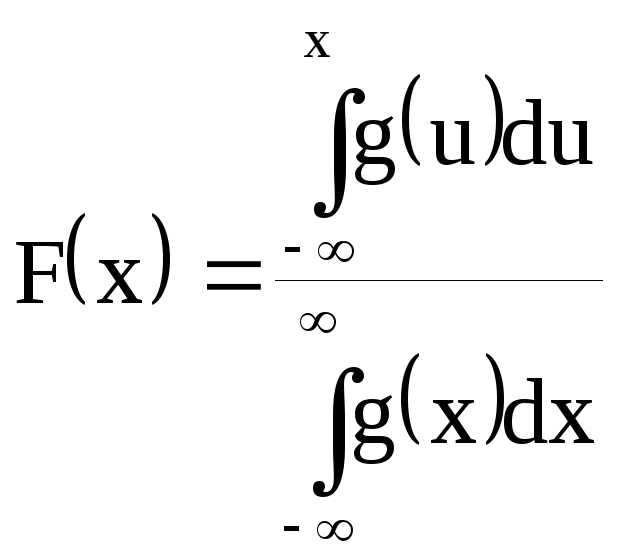
будет функцией распределения с плотностью

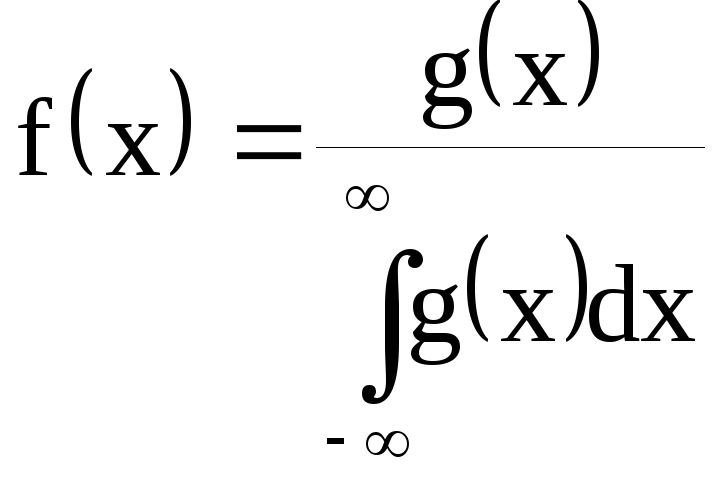
Этот факт позволяет построить множество примеров непрерывных функций распределения

Вероятностный смысл плотности распределения

Если плотность распределения непрерывна в точке x, то

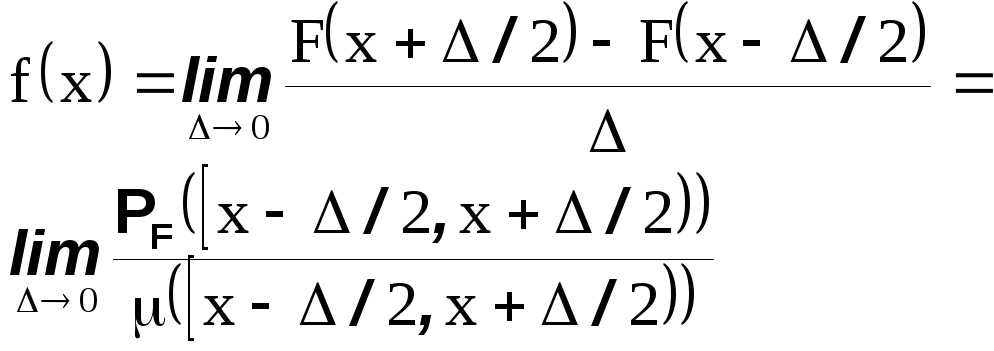
т.е. плотность это предельный коэффициент пропорциональности между вероятностью P и мерой Лебега. Отношение плотности в точке x к плотности в точке y показывает насколько вероятнее малая окрестность точки x такой же малой окрестности точки y. У равномерного распределения на отрезке [a,b] плотность постоянна на [a,b] ,т.е. все окрестности одинаковой длины имеют одинаковую вероятность. Это хорошо согласуется с представлением о совершенно случайном выборе точки из отрезка.

Бета-распределение на отрезке [0,1]

Связь между бета-функцией и гамма-функцией выражается соотношением

Рассмотрим функцию Эта функция неотрицательна, и при положительных a и b существует интеграл , который называется бета-функцияв точке (a,b).

Тогда функция

будет плотностью. Соответствующее ей распределение называется бета-распределениес параметрами (a,b) на отрезке [0,1].

В частном случае, при a=1 и b =1 получается равномерное распределение на отрезке [0,1]. Бета-распределение используется для моделирования ситуаций в которых точка случайно, но, вообще говоря, неравномерно выбирается из отрезка. Для того, чтобы понять, как устроено это распределение, построим график плотности бета-распределения при различных значениях параметров (a,b)

a=2 ,b=4

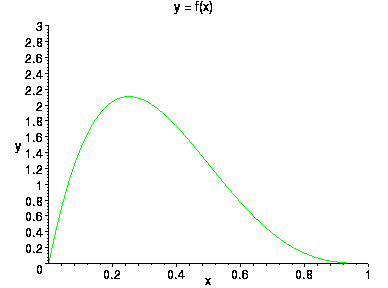
a=4 ,b=2

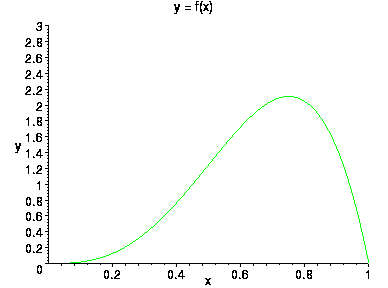
a=4 ,b=4

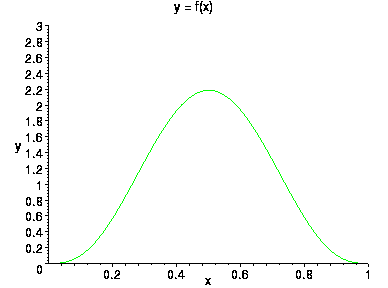
При a и b, больших единицы, плотность обращается в 0 на концах отрезка и имеет максимум в точке

Эта плотность подходит для моделирования ситуаций, в которых случайная точка имеет наибольшую вероятность находиться в окрестности точки x₀ , например, стрельба по отрезку, при которой точка x₀ является точкой прицеливания.

Придумайте примеры ситуаций, которые естественно описывать следующими бета-распределениями

При a и b, меньших единицы, вид плотности радикально меняется. a=1/2 , b=1/2

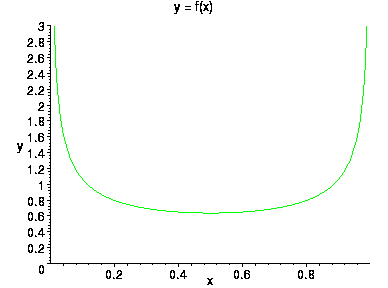
a=1/4 , b=2/3

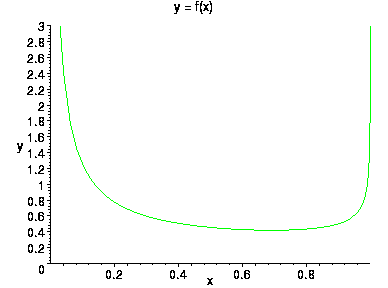
Наконец, приведем вид плотности бета-распределения при a=1/4 , b=4

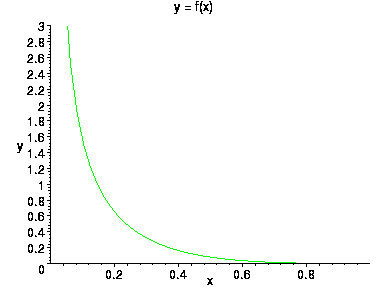
Для бета-распредления распределения используют обозначение

.