Советы по построению пространства элементарных исходов.

Имейте в виду задачу, которую вы хотите решить - то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию.

На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель.

Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны.

Очень удобно выбирать элементарные исходы в виде векторов (в смысле точек в пространстве), размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.

Определения Подмножества

Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.

• Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.

• Элементарный исход можно представить в виде

• ,

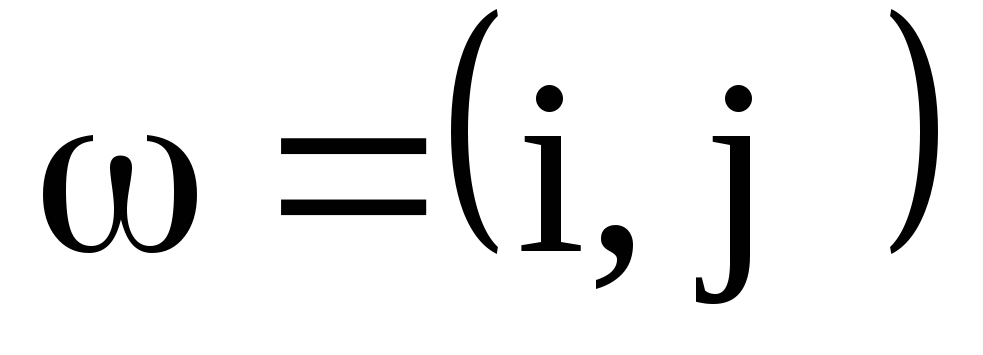• где i – число очков на первой кости, j – второй кости.

• Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:

• 

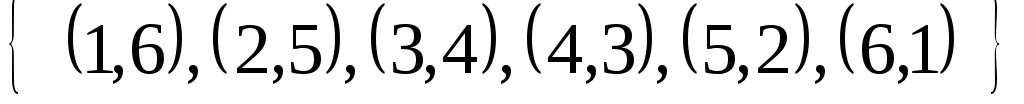
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…

A =

Пустое подмножество обозначим

Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.

Множество всех элементарных событий  называется, естественно, достоверное событие.

Элементарный исход как случайное событие представляет собой одноточечное подмножество.

Операции над подмножествами

Стандартные операции над подмножествами применяются в теории вероятностей и имеют вероятностную интерпретацию.

Дополнение

Дополнение до подмножества A - это подмножество

т. е. дополнением к Aявляется подмножество, включающее в себя все элементарные исходы, не содержащиеся вA. С точки зрения теории вероятностей подмножествоAпредставляет событие, которое естественно назвать отрицаниеAили не-A. Т.е.A в опыте не произошло («не наступило»).

Объединение

Объединением двух подмножеств AиBявляется подмножество

Соответственно и интерпретация : произошло или A илиB.

Пересечение

Пересечением двух подмножеств : AиBявляется подмножество

Соответственно и интерпретация : и A иB произошли одновременно.

Разность

Разностью двух подмножеств AиBявляется подмножество

Соответственно и интерпретация : A произошло,B - нет.

Симметричная разность

Симметричной разностью двух подмножеств AиBявляется подмножество

Соответственно и интерпретация : произошло только одно из этих двух событий.

Количество элементов в подмножестве

Если количество элементов в подмножестве A конечно, то будем обозначать его так

Отношения между подмножествами

Вложение

Подмножество В вложено в подмножествоA, если любой элементарный исход, содержащийся вBтакже содержится и вA.

Интерпретация:

Стрелкой будем пользоваться также и для утверждений типа: “из A следует B” в формулировках определений и теорем

из BследуетA

Т.е, если произошло B, то произошло и A.

Несовместность

Подмножества A и B называются несовместными (непересекающимися), если они не содержат общих элементарных исходов.

В теории вероятностей это означает, что A и B одновременно произойти не могут.

Противоположность

Подмножества A и B называются противоположными или дополнительными друг к другу, если они несовместны и их объединение достоверно.

В теории вероятностей это означает, что в опыте обязательно произойдет одно и только одно из этих событий.

Убывающая последовательность событий

Пусть

последовательность событий.

Она называется убываюшей, если каждое следующее событие этой последовательности вложено в предыдущее.

Аналогично можно определить возрастающую последовательность событий.

Формулы

Для доказательства равенства двух подмножеств AиBдостаточно показать, чтоAвложено вB,и чтоBвложено вA

Следующие формулы позволяют выразить одни операции с подмножествами через другие. Доказательства проведите сами.

Полная группа подмножеств

Полной группой подмножеств называется конечный набор или счетная последовательность попарно несовместных подмножеств объединение которых достоверно:

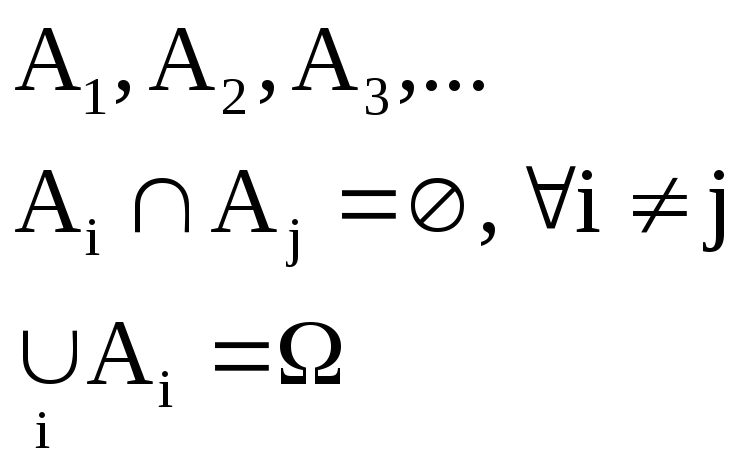
В опыте обязательно произойдет одно и только одно из этих событий.

Любые два противоположных подмножества образуют полную группу подмножеств.

Если пространство элементарных исходов конечно или счетно, то сами элементарные исходы являются полной группой подмножеств.

Алгебра и сигма-алгебра

При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:

Алгебра событий A это набор подмножеств пространства элементарных исходовдля которого выполняются следующие условия:

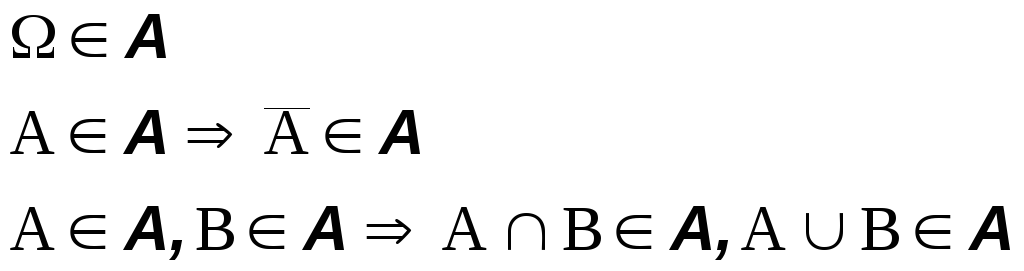
Сигма - алгебра событий F это набор подмножеств пространства элементарных исходовдля которого выполняются следующие условия:

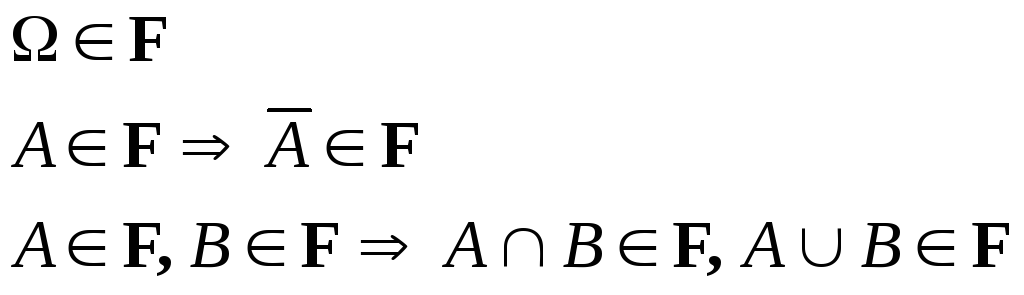
и для любой счетной последовательности

Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.

Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.

Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.

Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств

Если алгебра или сигма-алгебра содержит событие A , то она обязана содержать и отрицаниеA. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.

Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.