Теорема Радона-Никодима

Теорема.

Пусть - две сигма-конечные меры и. Тогда существует и единственна с точностью до значений на множествемеры нуль функциятакая, что

Единнственность с точностью до значений на множестве меры нуль означает, что если- другая функция, удовлетворяющая условию

, то

Случайная величина называется производной Радона-Никодима мерыотносительно мерыили плотностью мерыотносительно мерыи обозначается так

Если мера абсолютно непрерывна относительно меры, то можно заменять вычисление интеграла Лебега по мерена вычисление интеграла Лебега по мере, что показывает следующая лемма

Лемма.

Пусть - две сигма-конечные меры и. Тогда для любой случайной величины

Доказательство.

Для простых случайных величин равенство очевидно. Далее применяем теорему о монотонной сходимости.

Используя данную лемму, нетрудно показать, что если , то

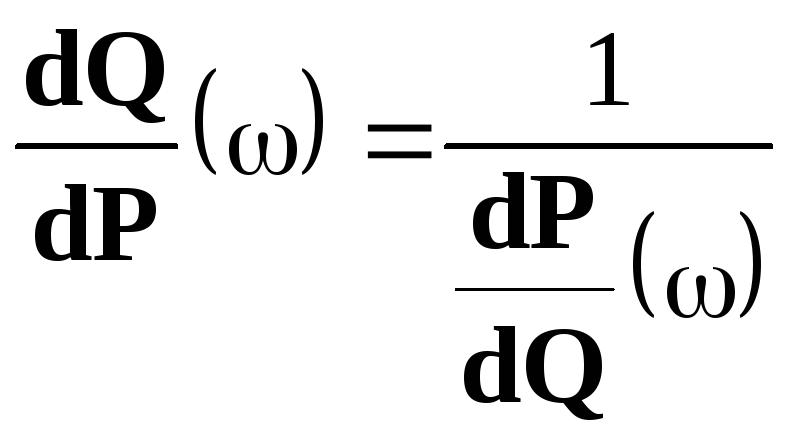
и если- три сигма-конечные мерыи, то

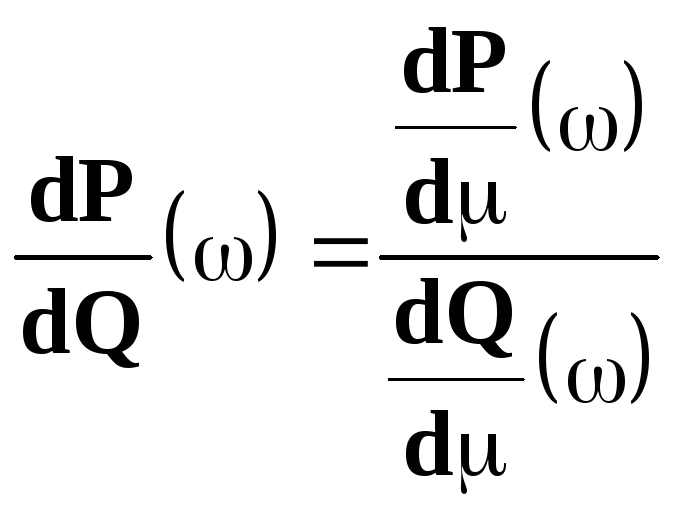
Приведем примеры абсолютно непрерывных, эквивалентных и сингулярных распределений и вычислим соответствующие плотности.

Пример 1.

Пусть -два дискретных распределения на одном и том же множестве значений

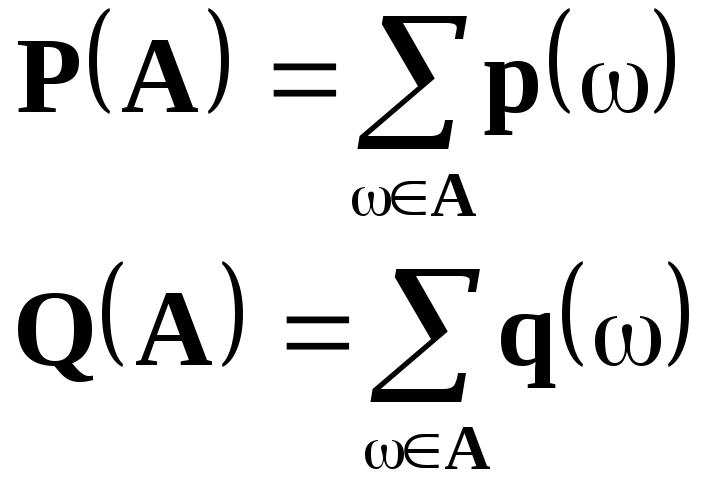
Тогда , если , тои для тех, для которых

для остальных можно определять плотность произвольным образом.

Если , то

В частности, любые два пуассоновских распределения эквивалентны, так как для распределения Пуассона величина

положительна при любых

Пример 2.

Пусть -два распределения на прямой с плотностями

Здесь - мера Лебега.

Напомним, что плотности определяются неоднозначно

Тогда , если существуют варианты плотностей такие, что , тои для тех, для которых

для остальных можно определять плотность произвольным образом.

Указание: покажите, что если на множествеA и, то

Доказательствопроведите самостоятельно.

В частности, если , то

Например, любые два нормальных распределения эквивалентны, так как для любого нормального распределения существует вариант плотности, который всюду больше нуля.

Пример 3.

Проверьте!

Равномерное распределение на отрезке абсолютно непрерывно относительно равномерного распределения на отрезке, если. Эти распределения эквивалентны тогда и только тогда , когда отрезки совпадают, и сингулярны когда отрезки не пересекаются.

Суммирование независимых случайных величин

Чрезвычайно важным объектом теории вероятностей является сумма независимых случайных величин. Именно исследования распределения сумм независимых случайных величин заложили фундамент для развития аналитических методов теории вероятностей.

Распределение суммы независимых случайных величин

В данном разделе мы получим общую формулу, позволяющую вычислить функцию распределения суммы независимых случайных величин, и рассмотрим несколько примеров.

Распределение суммы двух независимых случайных величин. Формула свертки

Пусть

независимые случайные величины с функциями распределения

соответственно

Тогда функцию распределения F суммы случайных величин

можно вычислить по следующей формуле (формула свертки)

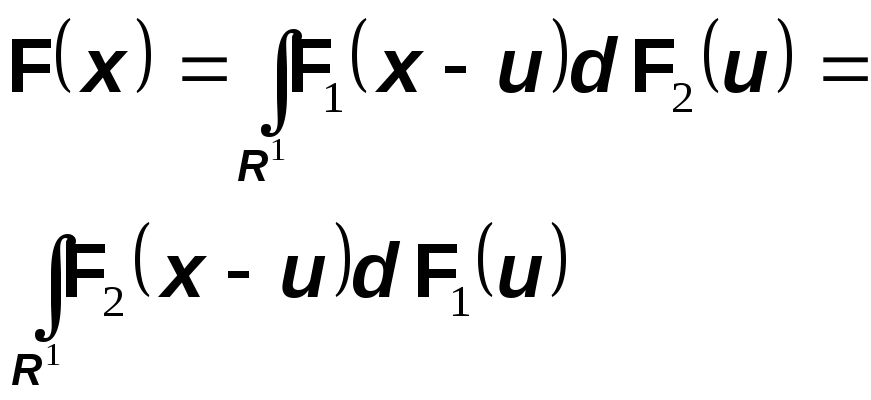
Для доказательства воспользуемся теоремой Фубини.

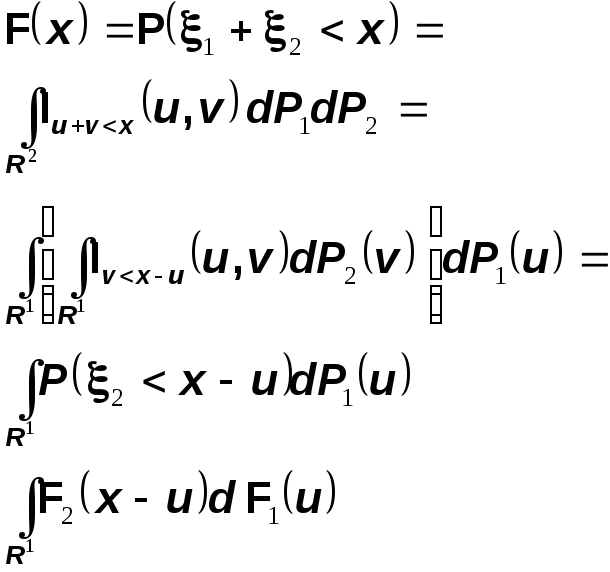
Аналогично доказывается вторая часть формулы.

Плотность распределения суммы двух независимых случайных величин

Если распределения обеих случайных величины имеют плотности, то плотность суммы этих случайных величин можно вычислить по формуле

Если распределение случайной величины (или) имеет плотность, то плотность суммы этих случайных величин можно вычислить по формуле

Для доказательства этих утверждений достаточно воспользоваться определением плотности.

Кратные свертки

Вычисление суммы конечного числа независимых случайных величин производится с помощью последовательного применения формулы свертки. Функция распределения суммы k независимых одинаково распределенных случайных величин с функцией распределенияF

называется k –кратной сверткой функции распределенияF и обозначается

Примеры вычисления распределения сумм независимых случайных величин

В этом пункте приведены примеры ситуаций, при суммировании случайных величин сохраняется вид распределения. Доказательства представляют собой упражнения на суммирование и вычисление интегралов.

Суммы независимых случайных величин. Нормальное распределение

Пусть

тогда

Суммы независимых случайных величин.Биномиальное распределение

Пусть

тогда

Суммы независимых случайных величин.Пуассоновское распределение

Пусть

тогда

Суммы независимых случайных величин.Гамма распределение

Пусть

тогда

Пуассоновский процесс

Пусть

последовательность независимых одинаково распределенных случайных величин, имеющих экспоненциальное распределение с параметром

Случайная последовательность точек

на неотрицательной полуоси называется пуассоновский (точечный) процесс.

Вычислим распределение числа точек

пуассоновского процесса в интервале (0,t)

События

эквиваленты, поэтому

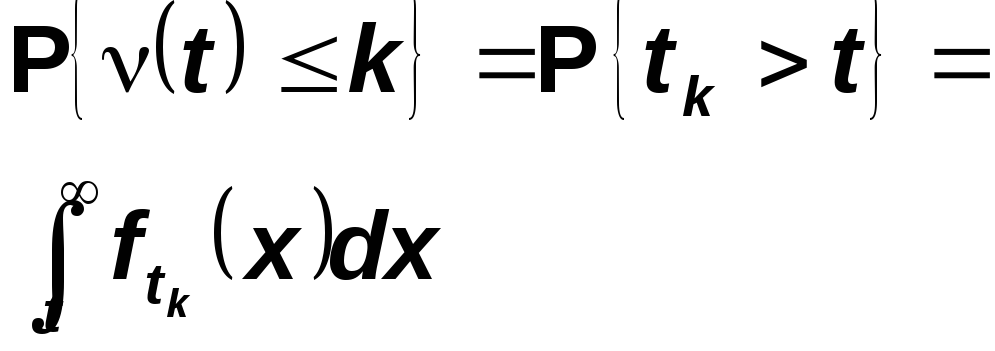
Но распределение случайной величины

является распределением Эрланга порядка k, поэтому

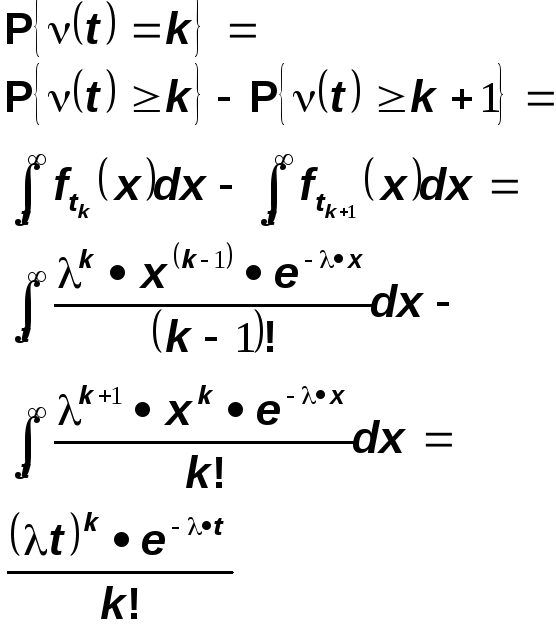
Таким образом распределение количества точек пуассоновского процесса в интервале (o,t)это пуассоновское распределение с параметром

Пуассоновский процесс используется для моделирования моментов наступления случайных событий – процесса радиоактивного распада, моментов поступления звонков на телефонную станцию, моментов появления клиентов в системе обслуживания, моментов отказа оборудования.