Вычисление математического ожидания.

Если случайная величина простая, то ее математическое ожидание вычисляется непосредственно по определению. Например, если все значения

случайной величины

равновероятны, то ее математическое ожидание равно среднему арифметическому этих значений

Заметим , что у простой случайной величины математическое ожидание всегда конечно.

Для дискретной случайной величины, принимающей счетное число различных значений, имеем (приближая ее снизу последовательностью простых случайных величин)

Этот ряд не всегда сходится, и поэтому существуют дискретные случайные величины, не имеющие конечного математического ожидания. Простым достаточным условием конечности математического ожидания является ограниченность модуля случайной величины сверху (константой или другой случайной величиной, имеющей конечное математическое ожидание).

Заметим, что для вычисления математического ожидания дискретной случайной величины нам достаточно знать только ее распределение. Этот факт справедлив и в общем случае, что показывает следующая теорема.

Теорема Лебега о замене переменных

Пусть

случайная величина и g(x) – борелевская функция

Тогда

если хотя бы один из этих интегралов существует.

Проверьте!

Доказательство. Легко проверить, что утверждение теоремы верно для неотрицательных простых функций.

Следовательно, в силу теоремы о монотонной сходимости оно верно и для произвольных неотрицательных случайных величин. Далее, как обычно представим произвольную случайную величину в виде разности

и завершим доказательство.

Заметим, что справа стоит интеграл Лебега по прямой. Поэтому, для эффективного вычисления произвольных интегралов Лебега, надо научиться вычислять

• распределения случайных величин

• интегралы Лебега на прямой

Как мы уже знаем, вычисление распределения на прямой эквивалентно вычислению его функции распределения. Поэтому займемся вторым пунктом.

Вычисление интеграла Лебега на прямой.

Так как на распределение на прямой однозначно определяется функцией распределения

то интеграл Лебега часто обозначают так

и называют интегралом Лебега-Стильтьеса от функции g по функции F.

Если функция распределения имеет плотность

то предыдущий интеграл интеграл превращается в интеграл

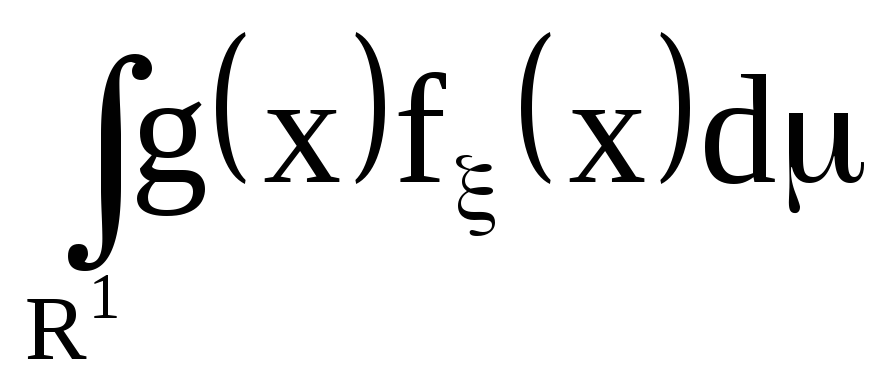
где

мера Лебега на прямой.

Для доказательства этого достаточно опять рассмотреть простые функции и перейти к пределу. Можно показать, что

если функция g (x) интегрируема по Риману, то

где последний интеграл понимается в смысле Римана.

Таким образом, в практически важных случаях вычисление интеграла Лебега сводится к вычислению конечной суммы, ряда или интеграла Римана (или их комбинаций). В дальнейшем для интегралов по мере Лебега будем опускать символ и использовать такое же обозначение как и для интегралов Римана.

Вычисление интеграла Лебега в произведении пространств. Теорема Фубини

В математическом анализе кратные интегралы часто вычисляются с помощью сведения их к повторным интегралам. Аналогично можно вычислять и интегралы Лебега, в тех случаях, когда основное вероятностное пространство является произведением вероятностных пространств.

Теорема Фубини

Пусть основное пространство является произведением двух пространств

и существует

Тогда

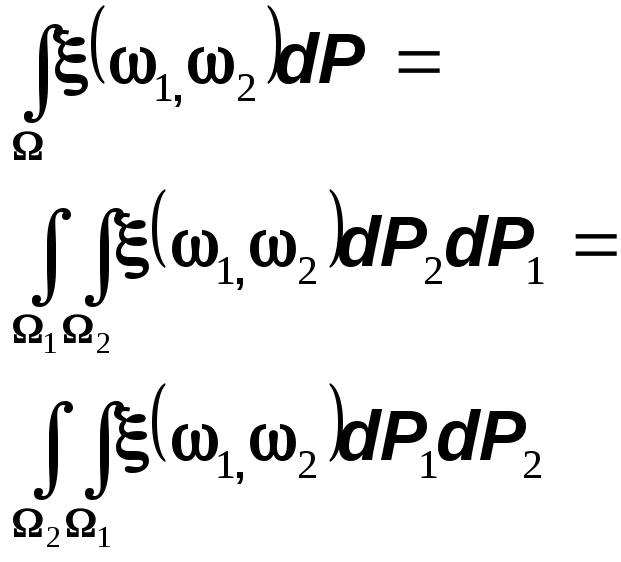
Теорема обобщается на любое конечное произведение вероятностных пространств. Доказательство можно найти, например, в книге Ширяева.