2.1. Локализация корней

Локализация корней – это процедура нахождения в области определения функции таких отрезков, на которых уравнение (2.1) имеет только один корень (одно решение). Для локализации корней уравнения (2.1) необходимо иметь критерий, позволяющий убедиться, что, во-первых, на некотором рассматриваемом отрезке 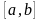числовой оси имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки (не равны нулю), то есть 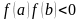, то на этом отрезке расположен по крайней мере один корень (нечетное число корней). Если 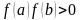, то на отрезке либо нет корней, либо их четное число, данный случай рассматриваться не будет.

Как видно из рис. 2.1, условие не обеспечивает единственности корня, но является необходимым условием его наличия. Достаточным условием, обеспечивающим единственность корня на отрезке , является требование монотонности функции на данном отрезке. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства ее производной 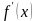. Заметим, что если на области определения функции отсутствуют точки, в которых ее производная равна нулю или не существует, то функция монотонна на всей области определения.

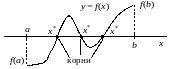
Рис. 2.1. Локализация корней. Функция не монотонна на отрезке .

Таким образом, если на отрезке функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки (не равны нулю), то на рассматриваемом отрезке существует один и только один корень соответствующего уравнения .

Число называется корнем кратности уравнения (2.1), если при 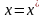вместе с функцией равны нулю ее производные до порядка 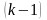: 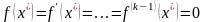. Корень кратности один называется простым.

Воспользовавшись рассмотренным критерием, составим общий алгоритм аналитической локализации корней нелинейного уравнения с одной переменной:

1. Вычисление первой производной функции .

2. Выявление на области определения функции интервалов монотонности, определяемых точками, в которых 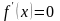или не существует.

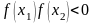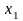3. Выбор среди интервалов монотонности тех, на концах которых значения функции имеют разные знаки, , где и 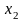– границы интервалов.

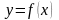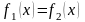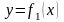Локализацию корней можно выполнить графически, если удается построить график функции и определить отрезки, на которых она имеет только одну точку пересечения с осью абсцисс. В ряде случаев бывает удобно заменить уравнение эквивалентным уравнением вида , корни которого определяются абсциссами точек пересечения графиков функций и 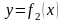. В качестве примера рассмотрим уравнение 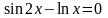. Перейдем к эквивалентному уравнению 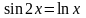и построим графики функци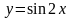й и 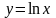(рис. 2.2).

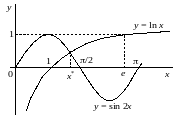
Рис. 2.2. Графическая локализация корней уравнения .

Из графиков, представленных на рис. 2.2, видно, что уравнение содержит один корень , расположенный в интервале .

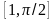Локализация корней может быть также выполнена табличным способом. Допустим, что корни уравнения (2.1) находятся на отрезке 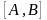оси . Выбор данного отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной задачи. Будем вычислять значения , начиная с точки 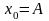, двигаясь вправо с некоторым шагом 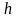(рис. 2.3). Получим набор значений функции 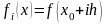, 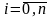. При обнаружении пары соседних значени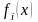й и 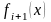, имеющих разные знаки (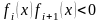 ), соответствующие значения аргумента можно считать границами отрезка, содержащего корень.

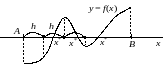
Рис. 2.3. Табличный подход к локализации корней.

Надежность табличного подхода к локализации корней уравнений зависит как от характера функции , так и от выбранной величины шага . Действительно, если при достаточно малом значении 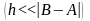на границах текущего отрезка 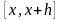функция принимает значения одного знака, то естественно ожидать, что уравнение корней на этом отрезке не имеет. Однако, это не всегда так. При несоблюдении условия монотонности функции на отрезке в его пределах могут оказаться корни уравнения (рис.2.4.а). Также на отрезке может располагаться несколько корней и при выполнении условия 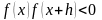(рис. 2.4.б).

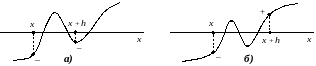
Рис 2.4. Наличие нескольких корней при несоблюдении условия монотонности функции: а) 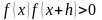; б) .

Предвидя подобные ситуации, следует выбирать достаточно малые значения , учитывая характер функции , например, с учетом значений . Поскольку табличный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может быть велико при малых значениях , то его целесообразно реализовывать на компьютере, но не рационально использовать при ручном счете. Локализуя корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность данного значения не будет превосходить половины шага 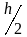. Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность локализации корней до любого наперед заданного значения, однако данный способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не целесообразен для уточнения корней и используется только для их локализации. Уточнение корней проводится с помощью других методов, более экономичных в плане вычислительных ресурсов.

В общем случае в связи с отсутствием гарантий надежности (рис. 2.4) табличный способ локализации корней практически не применяется на практике.