
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
Математически
условие сходимости можно установить
следующим образом. Представим приближения
и
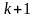 в форме
в форме
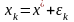 и
и
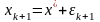 ,
где
,
где
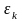 и
и
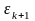 – отклонения приближений от корня.
Функцию
вблизи точки
приближенно заменим первыми двумя
членами ряда Тейлора, тогда итерационная
формула (2.11) примет вид
– отклонения приближений от корня.
Функцию
вблизи точки
приближенно заменим первыми двумя
членами ряда Тейлора, тогда итерационная
формула (2.11) примет вид
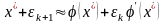 ,
,
но поскольку является корнем уравнения, то первые слагаемые в правой и левой частях этого выражения тождественно равны и, следовательно,
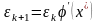 .
.
Для сходимости
итерационного процесса необходимо,
чтобы погрешность на каждом шаге убывала
(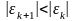 ),
откуда следует, что в окрестности корня
должно выполняться условие
),
откуда следует, что в окрестности корня
должно выполняться условие
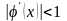 (то есть
(то есть
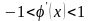 ). (2.12)
). (2.12)
Таким образом, для
того чтобы итерационный процесс (2.11)
был сходящимся, необходимо, чтобы
абсолютная величина производной
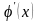 в окрестности корня была меньше единицы.
Если это условие выполняется на отрезке
локализации корня, то в качестве
начального приближения можно взять
любую точку, принадлежащую данному
отрезку (
).
в окрестности корня была меньше единицы.
Если это условие выполняется на отрезке
локализации корня, то в качестве
начального приближения можно взять
любую точку, принадлежащую данному
отрезку (
).
Переход от уравнения
(2.1) к уравнению в итерационной форме
(2.10) можно осуществить различными
способами в зависимости от вида функции
.
Необходимо построить функцию
так, чтобы выполнялось условие сходимости
(2.12). Рассмотрим один из общих алгоритмов
перехода от уравнения (2.1) к уравнению
(2.10). Умножим левую и правую части
уравнения (2.1) на произвольную константу
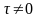 и добавим к обеим частям неизвестное
.
При этом корни исходного уравнения не
изменятся
и добавим к обеим частям неизвестное
.
При этом корни исходного уравнения не
изменятся
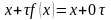 или
или
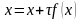 .
(2.13)
.
(2.13)
Уравнение (2.13)
эквивалентно уравнению (2.10), если
положить, что
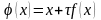 .
Произвольный выбор константы
.
Произвольный выбор константы
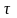 позволяет обеспечить выполнение условия
сходимости (2.12). Поскольку в данном
случае
позволяет обеспечить выполнение условия
сходимости (2.12). Поскольку в данном
случае
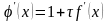 ,
значение
следует выбирать так, чтобы выполнялось
условие
,
значение
следует выбирать так, чтобы выполнялось
условие
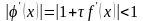 .
.
Желательно выбрать
величину
такой, чтобы
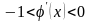 ,
тогда сходимость будет двухсторонней
(рис. 2.12.в). В этом случае в качестве
критерия окончания итерационного
процесса можно использовать соотношение
(2.6).
,
тогда сходимость будет двухсторонней
(рис. 2.12.в). В этом случае в качестве
критерия окончания итерационного
процесса можно использовать соотношение
(2.6).
Замечание.
При сходимости последовательных
приближений к корню с разных сторон,
что имеет место при
в окрестности корня (рис.2.12.в), величина
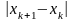 превосходит истинную погрешность, то
есть
превосходит истинную погрешность, то
есть
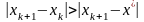 и критерий окончания итерационного
процесса (2.6) является объективным. Если
же
и критерий окончания итерационного
процесса (2.6) является объективным. Если
же
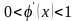 ,
то сходимость к корню носит односторонний
характер (рис. 2.11.а), и условие
может выполниться гораздо раньше
требования
,
то сходимость к корню носит односторонний
характер (рис. 2.11.а), и условие
может выполниться гораздо раньше
требования
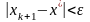 .
В этом случае контроль достигнутой
точности лучше осуществлять проверкой
неравенства
.
В этом случае контроль достигнутой
точности лучше осуществлять проверкой
неравенства
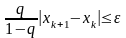 ,
где
,
где
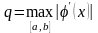 .
.
Наибольшая скорость
сходимости в методе итераций будет
наблюдаться при
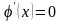 .
Этого можно добиться, выбрав параметр
зависящим
от
в виде
.
Этого можно добиться, выбрав параметр
зависящим
от
в виде
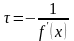 .
.
При этом итерационная формула (2.11) переходит в формулу Ньютона
.
Таким образом, метод Ньютона можно трактовать как частный случай метода итераций, обладающий максимальной скоростью сходимости.
2.2.7. Комбинированный метод хорд и касательных
Рассмотренные в данной главе методы хорд и касательных могут быть объединены в комбинированный метод, так как их совместное применение на каждой итерации позволит значительно быстрее сокращать длину отрезка локализации корня. Вместе с тем вычислительная сложность полученного комбинированного метода будет сопоставима с суммарной вычислительной сложностью методов хорд и касательных.
Пусть рассматривается
отрезок локализации корня
.
Комбинированный метод может быть
применен, если выполняются следующие
условия:
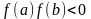 и
и
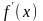 и
и
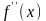 сохраняют знак на отрезке
.
При выполнении указанных условий
приближения к корню уравнения
сохраняют знак на отрезке
.
При выполнении указанных условий
приближения к корню уравнения
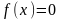 по методу хорд и по методу касательных
подходят к значению
данного корня с противоположных сторон.
Поэтому для быстроты нахождения корня
удобно применять оба метода одновременно.
Так как один метод даёт значение корня
с недостатком, а другой – с избытком,
то достаточно легко добиться заданной
точности. Схема решения нелинейного
уравнения комбинированным методом
включает следующие этапы:
по методу хорд и по методу касательных
подходят к значению
данного корня с противоположных сторон.
Поэтому для быстроты нахождения корня
удобно применять оба метода одновременно.
Так как один метод даёт значение корня
с недостатком, а другой – с избытком,
то достаточно легко добиться заданной
точности. Схема решения нелинейного
уравнения комбинированным методом
включает следующие этапы:
Вычисление значений функции
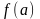 и
и
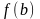 .
.Проверка выполнения условия . Если условие не выполняется, то отрезок выбран неправильно.
Нахождение производных и .
Проверка постоянства знаков производных на отрезке . Если нет постоянства знака, то отрезок выбран неверно.
Для метода касательных за выбирается тот из концов отрезка , где выполняется условие
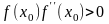 ,
то есть
,
то есть
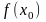 и
и
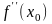 имеют один знак. Другой конец отрезка
выбирается для метода хорд, обозначим
его через
имеют один знак. Другой конец отрезка
выбирается для метода хорд, обозначим
его через
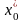 .
.Расчет приближения корней по каждому из методов:
а) по методу
касательных:
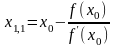 ;
;
б) по методу хорд:
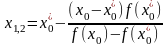 .
.
Вычисление первого приближения корня:
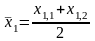 .
.Проверка выполнения условий:
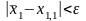 – для метода касательных;
– для метода касательных;
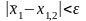 – для метода хорд;
– для метода хорд;
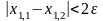 – для комбинированного метода. Здесь
– заданная точность вычисления корня.
Если какое-либо условие не выполняется,
то применение метода продолжается с
пятого шага для тех методов, условия
прекращения выполнения которых не
выполнены.
– для комбинированного метода. Здесь
– заданная точность вычисления корня.
Если какое-либо условие не выполняется,
то применение метода продолжается с
пятого шага для тех методов, условия
прекращения выполнения которых не
выполнены.
После первой
итерации отрезок локализации корня
сужается и принимает вид
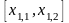 .
На второй итерации приближенные значения
корня для методов касательных и хорд
(в соответствии с пунктами 5 и 6)
рассчитываются соответственно по
формулам:
.
На второй итерации приближенные значения
корня для методов касательных и хорд
(в соответствии с пунктами 5 и 6)
рассчитываются соответственно по
формулам:
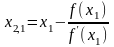 и
и
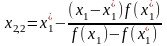 .
.
В общем случае
вычисления продолжаются, пока не будет
найдено такое приближение корня
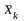 ,
при котором
,
при котором
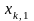 и
и
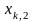 совпадут с точностью
совпадут с точностью
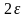 .
.
Формулы расчета приближений корня на итерации имеют вид
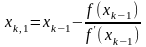 и
и
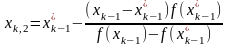 .
.
