
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
Результаты вычисления значений функции .
|
1 |
2,5 |
4 |
0 |
1,000 |
0,400 |
0,250 |
0,5 |
0,800 |
0,320 |
0,200 |
1 |
0,500 |
0,200 |
0,125 |
Формула (4.16) дает следующий результат:
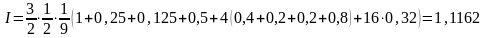 .
.
Между тем истинное
значение интеграла, рассчитанное
аналитически,
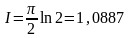 .
Таким образом, абсолютная погрешность
.
Таким образом, абсолютная погрешность
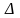 составит
составит
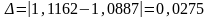 ,
а относительная –
,
а относительная –
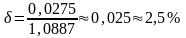 ,
хотя значения
и
довольно велики. Значительно большую
точность можно получить, разбив исходный
прямоугольник
на более мелкие прямоугольники, изменив
соответствующим образом и значения
коэффициентов.
,
хотя значения
и
довольно велики. Значительно большую
точность можно получить, разбив исходный
прямоугольник
на более мелкие прямоугольники, изменив
соответствующим образом и значения
коэффициентов.
Основным и неустранимым недостатком приближенной формулы (4.16) является то, что она применима лишь для прямоугольных областей со сторонами, параллельными координатным осям. Применение ее для других областей, например для круга, вызывает уже весьма серьезные затруднения.
Другим способом приближенного вычисления двойных интегралов являются формулы, в которых точки, где следует вычислять значения функции, задаются заранее специальным образом. Подбор данных точек производится так, чтобы полученная формула была точной для всех многочленов некоторой достаточно высокой степени при минимальном количестве этих точек.
Приведем формулу
такого рода. Обозначим через
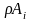 ,
,
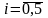 ,
точки, полярные координаты которых
,
точки, полярные координаты которых
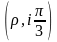 ,
тогда для единичного круга
имеет место следующая формула Люстерника:
,
тогда для единичного круга
имеет место следующая формула Люстерника:
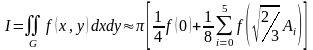 . (**)
. (**)
Таким образом, для
приближенного вычисления двойного
интеграла по кругу следует вычислить
значения функции в семи точках, одна из
которых лежит в центре круга. Остальные
точки лежат в вершинах правильного
шестиугольника, вписанного в окружность
радиуса
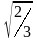 ,
их расположение представлено на рис.4.14,
причем возле каждой точки указан
коэффициент, на который нужно умножить
значение функции в соответствующей
точке.
,
их расположение представлено на рис.4.14,
причем возле каждой точки указан
коэффициент, на который нужно умножить
значение функции в соответствующей
точке.
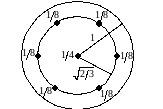
Рис. 4.14. Область интегрирования, представленная единичным кругом.
Очевидно, что с помощью подстановки легко преобразовать интеграл по любому кругу в интеграл по кругу радиуса 1, после чего для вычисления его значения можно воспользоваться указанной выше формулой Люстерника (**).
Если область интегрирования не прямоугольник и не круг, например,
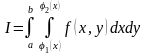 ,
,
где
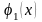 и
и
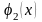 – произвольные функции, то для вычисления
двойного интеграла требуются другие
методы. Приведем общие рассуждения.
– произвольные функции, то для вычисления
двойного интеграла требуются другие
методы. Приведем общие рассуждения.
Для функции двух переменных рассмотрим случай произвольной области интегрирования , пример представлен на рис. 4.15.
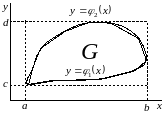
Рис. 4.15. Произвольная область интегрирования .
Заключим область
в прямоугольник со сторонами, параллельными
осям координат, и обозначим его через
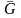 .
Для рассматриваемого интеграла значения
и
на рис. 4.15 определены следующим образом:
.
Для рассматриваемого интеграла значения
и
на рис. 4.15 определены следующим образом:
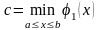 ,
,
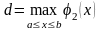 .
Введем в рассмотрение функцию
.
Введем в рассмотрение функцию
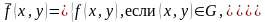
Тогда
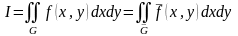 .
Интеграл по области
может быть вычислен по одному из описанных
выше алгоритмов. При этом точность
вычисления интеграла существенно
зависит от выбора области
и может быть повышена при изменении
шага интегрирования по осям. Границы
области
могут быть описаны с помощью кусочно-линейной
аппроксимации. При вычислении значения
функции
следует различать случаи, когда точка
.
Интеграл по области
может быть вычислен по одному из описанных
выше алгоритмов. При этом точность
вычисления интеграла существенно
зависит от выбора области
и может быть повышена при изменении
шага интегрирования по осям. Границы
области
могут быть описаны с помощью кусочно-линейной
аппроксимации. При вычислении значения
функции
следует различать случаи, когда точка
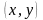 принадлежит и не принадлежит области
.
Общая идея определения данных случаев
будет рассмотрена далее.
принадлежит и не принадлежит области
.
Общая идея определения данных случаев
будет рассмотрена далее.
Особое место среди
методов вычисления кратных интегралов
занимают методы Монте-Карло (статистических
испытаний), рассматриваемые в разд. 4.8.
Изложим идею данных методов в самом
общем виде. Пусть область интегрирования
двойного интеграла представляет собой
не прямоугольник и не круг, тогда заключим
ее в прямоугольник, координаты углов
которого определяются точками
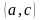 ,
,
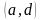 ,
,
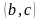 ,
,
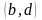 ,
аналогично рис. 4.15. На отрезках
и
будем генерировать значения равномерно
распределенных случайных величин
,
аналогично рис. 4.15. На отрезках
и
будем генерировать значения равномерно
распределенных случайных величин
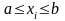 и
и
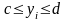 ,
,
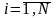 ,
где
– их количество. В результате будет
получено
точек
.
Исходя из геометрической вероятности,
отношение количества
точек, попавших в область
,
к общему числу точек
,
умноженное на площадь прямоугольника
со сторонами
и
,
где
– их количество. В результате будет
получено
точек
.
Исходя из геометрической вероятности,
отношение количества
точек, попавших в область
,
к общему числу точек
,
умноженное на площадь прямоугольника
со сторонами
и
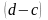 ,
будет являться значением искомого
интеграла. Заметим, что с ростом числа
генерируемых точек точность вычисления
значения интеграла будет возрастать,
а само количество точек должно быть
достаточно велико.
,
будет являться значением искомого
интеграла. Заметим, что с ростом числа
генерируемых точек точность вычисления
значения интеграла будет возрастать,
а само количество точек должно быть
достаточно велико.
Ключевым является
вопрос установления принадлежности
генерируемых точек
,
,
области
.
Аппроксимируем область
с помощью отрезков прямых линий,
соединяющих некоторые из ее граничных
точек, при этом число выбранных точек
должно быть достаточно велико. Введем
в рассмотрение некоторый полюс, например,
начало координат
 ,
и каждую генерируемую точку будем
соединять с ним прямой линией. Если
число пересечений данной линии с
отрезками прямых, аппроксимирующих
область
,
четно или равно нулю, то точка не
принадлежит области
,
а если нечетно, – то принадлежит.
Приведенные рассуждения проиллюстрированы
на рис. 4.16.
,
и каждую генерируемую точку будем
соединять с ним прямой линией. Если
число пересечений данной линии с
отрезками прямых, аппроксимирующих
область
,
четно или равно нулю, то точка не
принадлежит области
,
а если нечетно, – то принадлежит.
Приведенные рассуждения проиллюстрированы
на рис. 4.16.
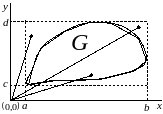
Рис. 4.16. Иллюстрация определения принадлежности точек области .
Приведенные выше рассуждения о способах вычисления двойных интегралов по области интегрирования общего вида (представленной не кругом и не прямоугольником), носят качественный характер. Прикладные вопросы вычисления кратных интегралов по непрямоугольным областям интегрирования в настоящем учебно-методическом пособии рассматриваться не будут.
