
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
4.7. Вычисление кратных интегралов
Для вычисления
кратных интегралов вида
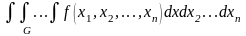 также используются численные методы.
В рамках данного учебно-методического
пособия ограничимся рассмотрением
двойных интегралов
также используются численные методы.
В рамках данного учебно-методического
пособия ограничимся рассмотрением
двойных интегралов
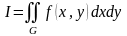 .
Будем
рассматривать неотрицательную непрерывную
функцию
.
Будем
рассматривать неотрицательную непрерывную
функцию
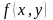 ,
заданную на квадрируемом (имеющем
площадь, ограниченном) множестве
,
заданную на квадрируемом (имеющем
площадь, ограниченном) множестве
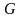 (области интегрирования) плоскости
(области интегрирования) плоскости
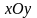 .
Определим разбиение
.
Определим разбиение
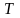 множества
как его представление в виде объединения
конечного числа
квадрируемых частей,
множества
как его представление в виде объединения
конечного числа
квадрируемых частей,
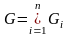 .
Можно считать, что разбиение
области
на части
.
Можно считать, что разбиение
области
на части
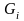 ,
,
определяется выбором геометрических
фигур, которыми представлены
,
.
,
,
определяется выбором геометрических
фигур, которыми представлены
,
.
В случае интегрирования
функции
рассматривались длины частей разбиения
отрезка
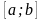 :
,
,
,
.
В случае интегрирования функции
обобщением понятия длины
будет площадь
:
,
,
,
.
В случае интегрирования функции
обобщением понятия длины
будет площадь
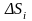 части
области
.
части
области
.
В каждой части
,
,
произвольным образом выберем точку
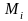 ,
имеющую координаты
,
имеющую координаты
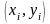 .
Обозначим
.
Обозначим
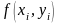 ,
,
через
.
Составим двумерную интегральную сумму
,
,
через
.
Составим двумерную интегральную сумму
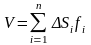 .
Очевидно, что каждое слагаемое полученной
суммы соответствует объему тела с
основаниями
и высотой
.
.
Очевидно, что каждое слагаемое полученной
суммы соответствует объему тела с
основаниями
и высотой
.
В разд. 4.1 было показано, что простая (одномерная) интегральная сумма в случае интегрирования функции на отрезке представляет собой площадь ступенчатой фигуры, составленной из прямоугольников c основаниями, соответствующими длинам частей разбиения отрезка , и с высотами, равными значениям функции в точках , выбранных на основаниях.
Аналогично,
двухмерная интегральная сумма
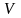 численно равна объему ступенчатого
тела, составленного из вертикальных
столбиков, имеющих части
,
,
области
своими основаниями, а значения функции
в некоторой принадлежащей им точке
равными высотам.
численно равна объему ступенчатого
тела, составленного из вертикальных
столбиков, имеющих части
,
,
области
своими основаниями, а значения функции
в некоторой принадлежащей им точке
равными высотам.
Очевидно, что для
заданной области
и непрерывной функции
можно составить не одну, а бесконечное
множество интегральных сумм, потому
что область
можно разбить на части
,
,
различными способами, а также по-разному
выбрать в них точки
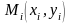 ,
.
В результате численная величина
интегральной суммы
зависит от способа разбиения области
и от выбора внутренних точек
в ее частях
,
.
,
.
В результате численная величина
интегральной суммы
зависит от способа разбиения области
и от выбора внутренних точек
в ее частях
,
.
Введем понятие
диаметра частей
–
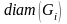 ,
значение которого определяется как
точная верхняя грань расстояния между
точками множества
.
В общем случае диаметром
,
значение которого определяется как
точная верхняя грань расстояния между
точками множества
.
В общем случае диаметром
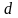 плоской фигуры
плоской фигуры
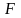 называется наибольшая из хорд данной
фигуры. Будем считать, что область
ограничена контуром
.
Предположим, что части
,
,
изменяются и начинают бесконечно
уменьшаться (не только в смысле величины
их площади, но и в смысле значений их
диаметров), так что даже самый большой
из их диаметров бесконечно уменьшается.
Это означает, что части
,
,
становятся все более малыми и так как
они должны заполнять постоянную площадь
внутри контура
,
то их число должно бесконечно увеличиваться.
С дугой стороны, непрерывная функция
является ограниченной и для всех точек
называется наибольшая из хорд данной
фигуры. Будем считать, что область
ограничена контуром
.
Предположим, что части
,
,
изменяются и начинают бесконечно
уменьшаться (не только в смысле величины
их площади, но и в смысле значений их
диаметров), так что даже самый большой
из их диаметров бесконечно уменьшается.
Это означает, что части
,
,
становятся все более малыми и так как
они должны заполнять постоянную площадь
внутри контура
,
то их число должно бесконечно увеличиваться.
С дугой стороны, непрерывная функция
является ограниченной и для всех точек
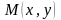 справедливо неравенство:
справедливо неравенство:
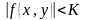 ,
,
где
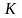 – постоянная величина. Отсюда следует,
что общий член
– постоянная величина. Отсюда следует,
что общий член
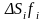 двухмерной интегральной суммы
имеет абсолютную величину, меньшую чем
двухмерной интегральной суммы
имеет абсолютную величину, меньшую чем
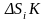 и, значит, бесконечно уменьшается.
и, значит, бесконечно уменьшается.
Таким образом, когда наибольший из диаметров частей , , бесконечно уменьшается, двухмерная интегральная сумма становится суммой бесконечно увеличивающегося числа слагаемых с бесконечно уменьшающимися значениями. В этих условиях двухмерная интегральная сумма стремится к определенному пределу, всегда одному и тому же, какую бы форму не имели бесконечно уменьшающиеся части , области , и каким бы образом ни выбирались в них точки , .
В рамках настоящего учебно-методического пособия доказательство данного важного предположения не приводится, однако его можно найти в более подробных курсах, посвященных интегральному исчислению.
Предел двухмерной интегральной суммы называется двойным (определенным) интегралом и обозначается следующим образом:
. (*)
Если областью
интегрирования
является прямоугольник (
,
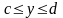 )
со сторонами, параллельными осям
координат, то для вычисления двойного
интеграла можно использовать любой из
рассмотренных в данной главе методов.
Например, применение формулы средних
прямоугольников при постоянном шаге
интегрирования дает следующий результат
)
со сторонами, параллельными осям
координат, то для вычисления двойного
интеграла можно использовать любой из
рассмотренных в данной главе методов.
Например, применение формулы средних
прямоугольников при постоянном шаге
интегрирования дает следующий результат

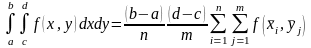 ,
,
где
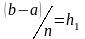 и
и
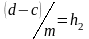 – шаги для отрезков интегрирования на
и
– шаги для отрезков интегрирования на
и
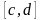 соответственно по
и
,
а
соответственно по
и
,
а
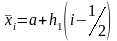 и
и
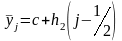 – средние точки отрезков интегрирования,
рис. 4.12.
– средние точки отрезков интегрирования,
рис. 4.12.
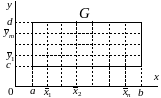
Рис. 4.12. Вычисление интеграла по прямоугольной области интегрирования.
Заметим, что с
повышением кратности интегралов резко
возрастает объем вычислений и рассмотренный
подход становится неэффективным.
Например, если мы разбиваем интервал
изменения каждой переменной всего на
десять частей, то для вычисления тройного
интеграла нам потребуется вычислить
сумму тысячи слагаемых, а при вычислении
десятикратного интеграла, потребуется
сумма, количество слагаемых в которой
определяется числом
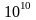 .
Вычисление такой суммы затруднительно
даже на самых быстродействующих
современных компьютерах. В этом случае
применяют другие методы численного
интегрирования, среди которых особое
место занимает метод статистических
испытаний (Монте-Карло), разд. 4.8.
.
Вычисление такой суммы затруднительно
даже на самых быстродействующих
современных компьютерах. В этом случае
применяют другие методы численного
интегрирования, среди которых особое
место занимает метод статистических
испытаний (Монте-Карло), разд. 4.8.
Остановимся на
общей идее получения формул вычисления
двойных интегралов, которая заключается
в их приведении к повторным интегралам
и последовательном применении формул
методов Ньютона-Котеса, например, формулы
Симпсона. Пусть требуется вычислить
двойной интеграл (*) по прямоугольнику
со сторонами, параллельными координатным
осям. Разобьем прямоугольник
на четыре равных прямоугольника средними
линиями и обозначим стороны данных
меньших прямоугольников соответственно
через
и
.
Значения функции
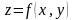 ,
вычисленные в узловых точках, обозначим
соответственно через
,
вычисленные в узловых точках, обозначим
соответственно через
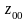 ,
,
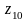 ,
,
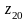 ,
,
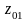 ,
,
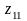 и т.д. Результат разбиения прямоугольной
области интегрирования представлен на
рис. 4.13.
и т.д. Результат разбиения прямоугольной
области интегрирования представлен на
рис. 4.13.
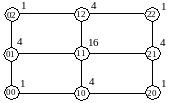
Рис. 4.13. Разбиение прямоугольной области интегрирования.
Тогда двойной интеграл (*) можно представить в виде
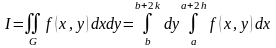
или
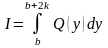 ,
где
,
где
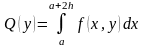 . (4.13)
. (4.13)
К каждому из полученных интегралов, в свою очередь, можно применить формулу Симпсона (4.8). Из (4.13) получим
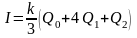 . (4.14)
. (4.14)
С другой стороны
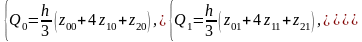 (4.15)
(4.15)
Подставив (4.15) в (4.14), получаем, что исходный интеграл (*) может быть вычислен по формуле
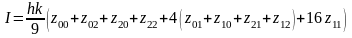 . (4.16)
. (4.16)
Таким образом, остается вычислить значения функции в узлах, номера которых отмечены в кружках на рис. 4.13.
Рассмотрим пример. Требуется вычислить интеграл
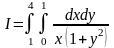 .
.
Решение.
Принимая
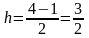 и
и
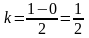 ,
вычислим значения функции
,
вычислим значения функции
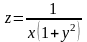 .
Результаты приведенны в табл. 4.1.
.
Результаты приведенны в табл. 4.1.
Таблица 4.1.
