1.7. Вопросы для самопроверки

1. Перечислите основные этапы исследования и математического моделирования явлений реального мира, раскройте их содержание.

2. Охарактеризуйте взаимосвязь этапов исследования и математического моделирования явлений, укажите их связь с численными методами.

3. Дайте определение численных методов, охарактеризуйте аналитические и приближенные методы.

4. Перечислите основные этапы решения математических задач с применением ЭВМ, раскройте их содержание и взаимосвязь.

5. Сформулируйте и поясните основные проблемы вычислительной математики.

6. Сформулируйте общую постановку задачи вычисления, дайте определение корректной задачи, раскройте ее содержание.

7. Охарактеризуйте понятие устойчивости решения задачи.

8. Перечислите основные источники погрешностей и раскройте их сущность.

9. Дайте определение абсолютной и относительной погрешности, приведите примеры.

10. Дайте определение значащих и верных цифр в записи чисел, приведите примеры.

11. Запишите формулы расчета абсолютной и относительной погрешности результата сложения чисел и , где и – их погрешности.

12. Запишите формулы расчета абсолютной и относительной погрешности результата вычитания чисел и , где и – их погрешности.

13. Запишите формулы расчета абсолютной и относительной погрешности результата умножения чисел и , где и – их погрешности.

14. Запишите формулы расчета абсолютной и относительной погрешности результата деления чисел и , где и – их погрешности.

15. Запишите формулы расчета абсолютной и относительной погрешности вычисления значения функции, зависящей от одного аргумента.

16. Объясните принцип представления чисел с плавающей точкой в памяти ЭВМ.

17. Каковы особенности выполнения арифметических операций над машинными числами?

18. Что является вершинами и дугами графа вычислительного процесса, значения каких параметров соответствуют его вершинам и дугам?

19. Приведите примеры графов вычислительных процессов основных математических операций, какие параметры соответствуют их дугам?

20. Объясните принцип расчета общей погрешности результата выполнения арифметических операций с помощью соответствующего графа вычислительного процесса, приведите пример.

Глава 2. Решение нелинейных уравнений с одной переменной

Решение нелинейных уравнений с одним неизвестным (одной переменной) является одной из важных математических задач, возникающих в различных разделах экономических и технических наук. В общем случае нелинейное уравнение с одним неизвестным можно записать в виде:

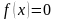, (2.1)

где 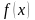– некоторая непрерывная функция аргумента , имеющая ограниченную или неограниченную область определения.

Всякое число 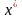, обращающее функцию в ноль, называется корнем уравнения (2.1). Как правило, при решении научных и инженерных задач функция содержит ряд параметров и исследователя интересует поведение решений уравнения 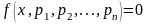(изменение значений его корней) в зависимости от изменения параметров 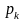, 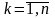. В таких случаях, не нарушая общности задачи, можно поменять местами неизвестное и любой из параметров , то есть решать уравнение относительно другой неизвестной величины.

Нелинейные уравнения с одним неизвестным подразделяются на алгебраические и трансцендентные (далее в тексте данные виды уравнений обобщены понятием нелинейных уравнений).

Уравнение (2.1) называется алгебраическим, если функция является алгебраической функцией 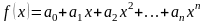. Алгебраическое уравнение всегда может быть представлено в канонической форме:

,

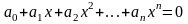где 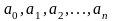– коэффициенты уравнения, а максимальный показатель степени – степень алгебраического уравнения.

Всякий многочлен степени имеет корней, действительных или комплексных. Комплексным называется число 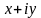, где 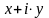и – вещественные числа, а – мнимая единица, .

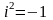Если функция не является алгебраической, то уравнение (2.1) называется трансцендентным, причем в зависимости от вида оно называется тригонометрическим, логарифмическим, показательным. Например, 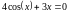, , 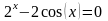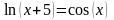. В некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических уравнений. Заметим, что уравнения и 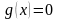называются равносильными (эквивалентными), если множества их решений совпадают.

Методы решения нелинейных уравнений подразделяются на прямые (аналитические, точные) и итерационные (численные). Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по данной формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для алгебраического уравнения выше четвертой степени с целыми или вещественными коэффициентами не удается получить аналитическое решение в радикалах (в виде формулы с конечным числом арифметических действий). В таких случаях приходится обращаться к численным методам, позволяющим получить приближенные значения корней с некоторой заданной точностью. К таким случаям следует отнести также те, в которых формулы для получения точного решения существуют, но столь громоздки, что использование приближенных методов оказывается предпочтительным (например, решение алгебраических уравнений третьей, четвертой и последующих степеней).

При применении численных методов задача решения нелинейного уравнения разбивается на два этапа: локализация (отделение) корней, то есть нахождение таких отрезков на оси 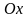(в области определения функции), в пределах которых содержится единственный корень, и уточнение корней, то есть вычисление приближенных значений корней с заданной точностью. Фактически решить нелинейное уравнение (2.1) означает: установить, имеет ли оно корни, определить число корней, установить отрезки локализации корней и найти значения корней с заданной точностью.