3.2.1. Прямой метод

Пусть на интерполяционной сетке заданы значения некоторой функции: 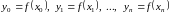. Требуется построить полином степени не выше , такой чтобы выполнялись условия, позволяющие однозначно определить значения его коэффициентов:

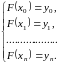(3.11)

Геометрически процесс замены таблично заданной функции интерполянтом заключается в проведении графика функции через все узловые точки функции (рис. 3.1).

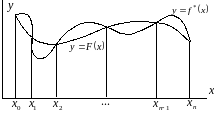
Рис. 3.1. Интерполирование функции .

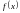На рис. 3.1 помимо графика интерполянта представлен график функции 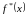, также проведенный через все узловые точки , , функции , но, очевидно, являющийся неудачным результатом ее интерполяции.

Если не указан класс функции (не описаны ее свойства), то задача интерполирования не является корректной, так как отсутствие информации о характере поведения функции между узлами может привести к непредсказуемым погрешностям при построении интерполянта . На ЭВМ в качестве интерполянтов обычно используются полиномы степени не выше . В этом случае система уравнений (3.11) превращается в систему уравнений для неизвестных коэффициентов :

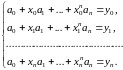(3.12)

Система (3.12) состоит из 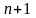уравнения и неизвестного и имеет единственное решение, которым являются значения коэффициентов интерполянта .

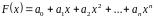Единственность решения доказывается тем, что определитель данной системы, так называемый определитель Вандермонда, отличен от нуля

.

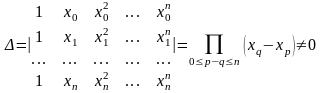Единственность решения означает, что разные способы вычисления коэффициентов интерполянта дают в результате один и тоже полином.

Рассмотрим пример. Пусть рассматриваются три узла интерполяционной сетки, в которых известны значения некоторой функци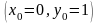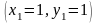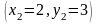и: , , . Требуется интерполировать функцию полиномом второй степени 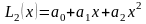, определив его коэффициенты .

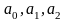Решение. На основании исходных данных известно, что 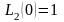, , 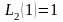а 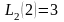, составим систему уравнений (3.12) для определения значений коэффициентов прямым методом:

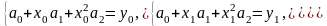
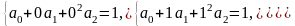
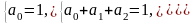
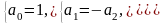
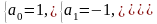
В результате получаем ответ: .

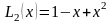3.2.2. Полином Лагранжа

Для построения интерполяционного многочлена прямым методом необходимо предварительно решить систему уравнений (3.12). Интерполяционная формула Лагранжа не требует решения системы (3.12) и в общем виде соответствующий полином можно представить следующей формулой:

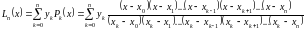, (3.13)

где 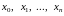– узлы интерполяционной сетки, а 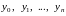– значения функции в соответствующих узловых точках.

Заметим, что многочлен 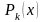удовлетворяет следующему требованию:

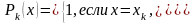
Многочлен равен нулю в точках 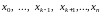, а в точке 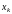равен единице. Это обеспечивает требование прохождения интерполяционного многочлена через все узлы интерполяционной сетки.

Каждое из слагаемых формулы (3.13) является полиномом степени не выше , следовательно, 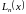также есть полином степени не выше . Формула (3.13) составлена так, чтобы выполнялось условие 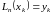. Если функция достаточно гладкая, то есть имеет непрерывные производные вплоть до порядка включительно, то погрешность интерполяции, определяемую формулой 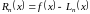, можно оценить следующим образом:

,

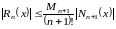где , .

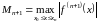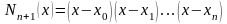Рассмотрим пример. Пусть рассматриваются три узла интерполяционной сетки, в которых известны значения некоторой функции: , , . Требуется интерполировать функцию полиномом Лагранжа второй степени .

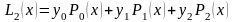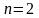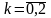Решение. На основании исходных данных известно, что и , определим 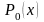, 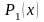и :

;

;

.

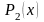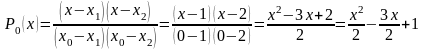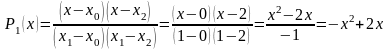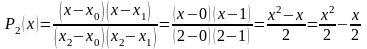В результате

.

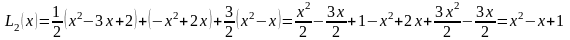Получаем ответ: 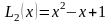(полученный в данном примере результат совпадает с результатом, полученным ранее при интерполировании функции прямым методом, однако, в общем случае совпадение результатов может и не наблюдаться).