
- •Глава 1. Численные методы и особенности использования эвм
- •Глава 2. Решение нелинейных уравнений с одной переменной 23
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций 47
- •Глава 4. Численное интегрирование 75
- •Глава 5. Приближенное интегрирование дифференциальных уравнений 108
- •Глава 6. Численное дифференцирование 139
- •Глава 7. Методы численной оптимизации 150
- •Предисловие
- •Глава 1. Численные методы и особенности использования эвм в решении математических задач
- •1.1. Математическое моделирование и численные методы
- •1.2. Общая постановка и понятие устойчивости задач вычисления
- •1.3. Структура погрешности решения задач вычисления
- •1.4. Абсолютная и относительная погрешности
- •Пример 1.4. Примеры записи абсолютной погрешности числа :
- •Пример 1.5. Пример записи относительной погрешности числа :
- •1.5. Погрешность машинных вычислений и представлений чисел в памяти эвм
- •1.6. Графы вычислительных процессов
- •1.7. Вопросы для самопроверки
- •Глава 2. Решение нелинейных уравнений с одной переменной
- •2.1. Локализация корней
- •2.2. Уточнение корней
- •2.2.1. Метод половинного деления (бисекции, дихотомии)
- •2.2.2. Метод хорд
- •2.2.3. Метод Ньютона (касательных)
- •2.2.4. Модифицированный метод Ньютона
- •2.2.5. Метод секущих
- •2.2.6. Метод итераций
- •Б) односторонний расходящийся процесс; в) двухсторонний сходящийся процесс; г) двухсторонний расходящийся процесс.
- •2.2.7. Комбинированный метод хорд и касательных
- •2.3. Вопросы для самопроверки
- •Глава 3. Методы приближения, интерполяции и аппроксимации функций
- •3.1. Методы приближения функций
- •3.1.1. Формула Тейлора, ряд Тейлора
- •3.1.2. Полиномы Чебышева
- •3.1.3. Экономизация степенных рядов
- •3.1.4. Приближения с помощью дробно-рациональных функций
- •3.2. Методы интерполяции функций
- •3.2.1. Прямой метод
- •3.2.2. Полином Лагранжа
- •3.2.3. Полином Ньютона
- •Конечные разности функции .
- •3.3. Методы аппроксимации функций
- •3.3.1. Среднеквадратичная аппроксимация
- •Некоторые регрессионные модели.
- •Премиальные фонды и прибыли предприятий
- •Расчет сумм для проведения регрессионного анализа
- •Коэффициенты регрессии
- •Расчет суммы квадратов отклонений по линейной модели
- •Сумма квадратов отклонений для рассматриваемых моделей
- •3.3.2. Полиномиальная аппроксимация
- •3.3. Вопросы для самопроверки
- •Глава 4. Численное интегрирование
- •4.1. Понятие определенного интеграла
- •4.2. Классификация методов численного интегрирования
- •4.3. Методы Ньютона-Котеса
- •4.3.1. Методы прямоугольников
- •4.3.2. Метод трапеций
- •4.3.3. Метод Симпсона (метод парабол)
- •4.4. Погрешность методов Ньютона-Котеса
- •4.5. Вычисление интегралов с заданной точностью
- •4.6. Особые случаи численного интегрирования
- •4.7. Вычисление кратных интегралов
- •Результаты вычисления значений функции .
- •4.8. Методы Монте-Карло
- •4.9. Вопросы для самопроверки
4.3.2. Метод трапеций
На каждом частичном
отрезке интегрирования
,
,
заменим подынтегральную функцию
полиномом первой степени
– прямой линией, проходящей через точки
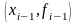 и
:
и
:
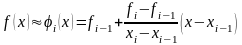 ,
.
,
.
Пояснение.
В общем виде уравнение прямой линии,
проходящей через две точки
и
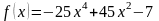 ,
задается следующим образом:
,
задается следующим образом:
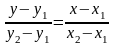 ,
откуда
,
откуда
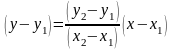 .
.
Подставляя полученное выражение в формулу (4.1) и выполняя интегрирование по частичным отрезкам, приходим к формуле трапеций:
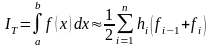 ,
.
,
.
На отрезках
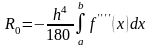 ,
,
площадь под графиком функции
заменяется площадями трапеций с
основаниями, равными значениям функции
,
,
площадь под графиком функции
заменяется площадями трапеций с
основаниями, равными значениям функции
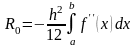 на концах отрезка, и высотой, равной
на концах отрезка, и высотой, равной
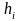 (рис. 4.7).
(рис. 4.7).
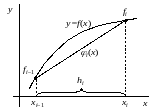
Рис. 4.7. Иллюстрация метода трапеций.
В случае постоянного
шага интегрирования, когда
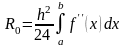 ,
,
формула трапеций принимает вид
,
,
формула трапеций принимает вид
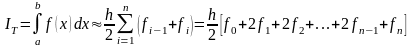 . (4.6)
. (4.6)
Для удобства вычислений формулу (4.6) записывают следующим образом:
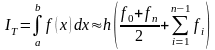 .
.
Вид представленной
формулы позволяет сделать вывод, что
она может быть сформирована также исходя
из других соображений, так как получаемый
с ее применением результат является
средним арифметическим результатов
использования формул левых (4.3) и правых
(4.4) прямоугольников. Поэтому
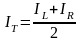 и указанное утверждение справедливо
для случаев равных и неравных шагов
интегрирования.
и указанное утверждение справедливо
для случаев равных и неравных шагов
интегрирования.
Замечание. Несмотря на то, что в методе трапеций для аппроксимации подынтегральной функции используются полиномы первой степени, по сравнению с методами прямоугольников, которые используют полиномы нулевой степени, точность метода трапеций оказывается ниже точности метода средних прямоугольников. Более высокая точность метода средних прямоугольников объясняется «удачным» выбором узловых точек для вычисления значений подынтегральной функции.
4.3.3. Метод Симпсона (метод парабол)
Аппроксимацию
функции
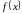 по методу трапеций можно интерпретировать
как замену исходной функции
некоторой кусочно-линейной функцией.
Ошибка метода в данном случае определяется
«грубостью» предложенного способа
аппроксимации функции. Естественно
допустить, что если исходную функцию
аппроксимировать на частичных отрезках
не линейными функциями, а полиномами
более высоких порядков, то ошибка
соответствующего метода численного
интегрирования должна уменьшиться. В
методе Симпсона в
качестве функции, с помощью которой на
частичных отрезках интегрирования
заменяется исходная функция
,
выбрана парабола.
по методу трапеций можно интерпретировать
как замену исходной функции
некоторой кусочно-линейной функцией.
Ошибка метода в данном случае определяется
«грубостью» предложенного способа
аппроксимации функции. Естественно
допустить, что если исходную функцию
аппроксимировать на частичных отрезках
не линейными функциями, а полиномами
более высоких порядков, то ошибка
соответствующего метода численного
интегрирования должна уменьшиться. В
методе Симпсона в
качестве функции, с помощью которой на
частичных отрезках интегрирования
заменяется исходная функция
,
выбрана парабола.
Пояснение.
Более высокая точность вычисления
интегралов обеспечивается при
использовании параболической аппроксимации
(полиномом второй степени)
по трем соседним точкам. Для нахождения
коэффициентов
,
и
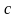 полинома, проходящего через точки
,
,
полинома, проходящего через точки
,
,
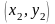 ,
требуется найти решение следующей
системы линейных уравнений
,
требуется найти решение следующей
системы линейных уравнений
относительно неизвестных , , .
Разделим отрезок
интегрирования
на четное число
равных отрезков с шагами
.
На каждом отрезке
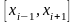 длиной
длиной
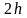 ,
содержащем три узла
,
содержащем три узла
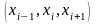 ,
заменим подынтегральную функцию
полиномом второй степени
,
заменим подынтегральную функцию
полиномом второй степени
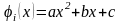 .
Пример представлен на рис. 4.8.
.
Пример представлен на рис. 4.8.
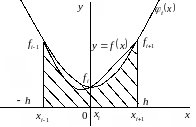
Рис. 4.8. Пример замены функции параболой.
Для рассматриваемого примера значения коэффициентов , и могут быть вычислены следующим образом:
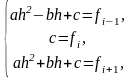
откуда
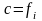 ,
,
,
,
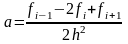 ,
а
,
а
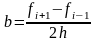 .
.
В результате рассматриваемый полином второй степени примет вид
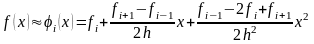 .
.
Интегрируя приведенное выражение на отрезке , получим
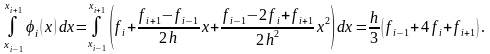 (4.7)
(4.7)
Приближенное значение интеграла на исходном отрезке интегрирования получим суммированием частичных интегралов (4.7) по всем отрезкам :
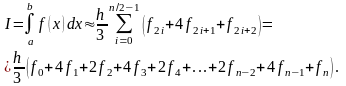 (4.8)
(4.8)
Полученное соотношение называется формулой Симпсона или формулой парабол, в соответствии с которой искомый определенный интеграл вычисляется как суммарная площадь параболических сегментов на всех частичных отрезках интегрирования .
Если подынтегральную функцию заменять полиномом второй степени на отрезках , , с привлечением дополнительных точек , – середин данных отрезков, то число отрезков разбиения может быть любым (не обязательно четным), а формула (4.8) будет иметь вид
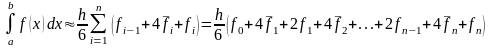 .
(4.9)
.
(4.9)
Напомним, что
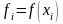 ,
,
,
,
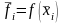 ,
.
,
.
Замечание 1. Формула (4.8) может быть использована для вычисления интегралов от функций, заданных как аналитическим выражением, так и таблично, тогда как формула (4.9) применима только в тех случаях, когда подынтегральная функция задана аналитически.
Замечание 2. Рассмотренные формулы, используемые для приближенного вычисления интегралов, называются квадратурными формулами. Нетрудно заметить, что все рассмотренные выше формулы имеют следующую структуру:
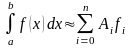 ,
,
где
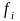 – значения подынтегральной функции в
узловых точках
,
а
– весовые коэффициенты.
– значения подынтегральной функции в
узловых точках
,
а
– весовые коэффициенты.
