2.2.2. Метод хорд

Рассматриваемый метод, как и метод половинного деления, предназначен для уточнения корня на отрезке , на концах которого функция принимает значения разных знаков, а на самом отрезке непрерывна и монотонна. Очередное приближение , в отличие от метода половинного деления, выбирается не в середине отрезка , а в точке, где ось абсцисс пересекается прямой линией (хордой), проведенной через точк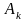и и 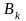, имеющие соответственно координаты 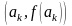, 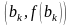(рис. 2.7).

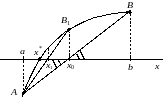
Рис. 2.7. Иллюстрация метода хорд.

Запишем уравнение прямой линии (хорды), проходящей через точк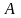и и :

.

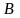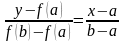Для отыскания точки пересечения хорды с осью абсцисс 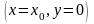получим уравнение

.

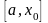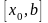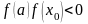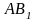В качестве нового отрезка для продолжения итерационного процесса выбирается тот из двух отрезков и , на концах которого функция принимает значения разных знаков. Для рассматриваемого случая (рис. 2.7) выбираем отрезок , так как . Следующая итерация состоит в определении нового приближения как точки пересечения хорды с осью абсцисс и так далее. Процесс уточнения корня заканчивается, когда расстояние между очередными приближениями станет меньше заданной точности, то есть

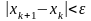, (2.6)

или при выполнении условия (2.5).

Замечание. Метод половинного деления и метод хорд очень похожи, в частности, процедурой проверки знаков функции на концах отрезка, при этом второй из них в ряде случаев дает более быструю сходимость итерационного процесса, хотя также обладает линейной скоростью сходимости. Кроме этого, оба рассмотренных метода не требуют знания дополнительной информации о функции , например, не требуется чтобы функция была дифференцируемой. Непрерывность функции на отрезке гарантирует сходимость данных методов. Более сложные методы уточнения корня используют дополнительную информацию о функции , прежде всего свойство дифференцируемости. В результате они обычно обладают более быстрой сходимостью, но применимы для более узкого класса функций и их сходимость не всегда гарантирована. Примером данных методов служит метод Ньютона (касательных).

Замечание. Метод хорд иногда называют также методом пропорциональных частей: корень ближе к тому из концов отрезка его локализации, в котором модуль значения ординаты меньше. Данное утверждение основано на подобии треугольников 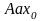и 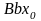(рис. 2.7). В то же время данное утверждение не всегда верно, так как возможны случаи, аналогичные представленному на рис. 2.8.

Рис. 2.8. Нарушение пропорциональности частей отрезка локализации корня.

2.2.3. Метод Ньютона (касательных)

Для данного метода предполагается, что и отличны от нуля и сохраняют знак на отрезке локализации корня. Пусть известно начальное приближение к корню (вопрос выбора начального приближения будет подробно рассмотрен далее). Проведем в данной точке касательную к графику функции (рис. 2.9).

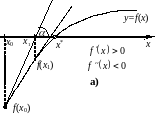
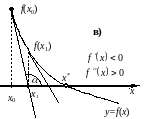
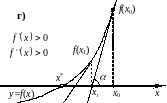
Рис. 2.9. Иллюстрации метода Ньютона.

Касательная к графику функции в точке 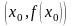пересекает ось абсцисс в точке , которую будем рассматривать в качестве следующего приближения. Значение (на основании рис. 2.9) может быть рассчитано следующим образом:

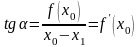, выражая , получим .

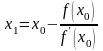Аналогично могут быть найдены и следующие приближения. Формула для вычисления приближения 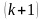имеет вид

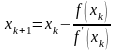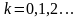_, . (2.7)

Из формулы (2.7) следует условие применимости метода: функция должна быть дифференцируемой и в окрестности корня не должна менять знак ( должна быть монотонной). В качестве условий окончания итерационного процесса может быть использовано условие (2.5) или (2.6).

Замечание. В методе Ньютона, в отличие от методов половинного деления и хорд, не обязательно задавать отрезок , содержащий корень уравнения, а достаточно найти некоторое начальное приближение корня на интервале, где выполняются условия монотонности и непрерывности функции.

Замечание. Формула метода Ньютона может быть получена и из других соображений. Зададимся некоторым начальным приближением корня . Заменим функцию в окрестности точки некоторым количеством первых слагаемых результата ее разложения в ряд Тейлора, например

,

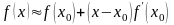и вместо нелинейного уравнения решим линеаризованное уравнение

,

которое, вообще говоря, является уравнением касательной к графику функции в точке начального приближения корня . Рассмотрим решение данного уравнения как следующее (первое) приближение к искомому значению корня. Решение уравнения очевидно:

.

Повторяя рассмотренный процесс, приходим к формуле Ньютона (2.7).

Пояснение. Ряд Тейлора для функции в окрестности точки имеет вид

.

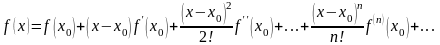Исследуем сходимость метода Ньютона. Выясним основные условия сходимости последовательности значений , вычисляемых по формуле (2.7), к корню уравнения (2.1). Предполагая, что дважды непрерывно дифференцируема, разложим 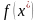в ряд Тейлора в окрестности приближения

.

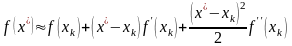В результате уравнение примет вид

.

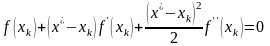Разделив полученное соотношение на 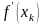и перенеся часть слагаемых из левой части в правую, получим:

.

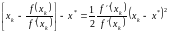Учитывая, что выражение в квадратных скобках, согласно формуле (2.7), равно , получаем

.

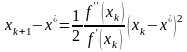В результате справедлива следующая оценка:

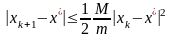, (2.8)

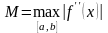где , а .

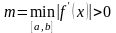Очевидно, что ошибка вычисления корня убывает, если

.

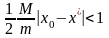Полученное условие означает, что сходимость метода Ньютона зависит от выбора начального приближения корня . Оценка (2.8) характеризует скорость убывания погрешности для метода Ньютона: на каждом шаге погрешность пропорциональна квадрату погрешности на предыдущем шаге. Следовательно, метод Ньютона обладает квадратичной сходимостью.

Рассмотрим принцип выбора начального приближения в методе Ньютона. Как следует из приведенных выше соотношений, сходимость итерационной последовательности, получаемой в методе Ньютона, зависит от выбора начального приближения . Это можно заметить и из геометрической интерпретации метода. Так, если в качестве начального приближения взять точку 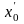, а не (рис. 2.10), то сходимость итерационного процесса не гарантируется. Это обусловлено тем, что получаемое приближение корня может не принадлежать отрезку его локализации или интервалу монотонности и непрерыности функции.

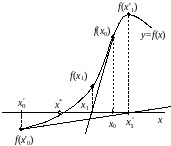
Рис. 2.10. Пример отсутствия сходимости метода Ньютона.

Если в качестве начального приближения выбрать точку , то получим сходящуюся последовательность. В общем случае, если задан отрезок , содержащий корень, и известно, что функция монотонна на данном отрезке, то в качестве начального приближения можно выбрать ту границу отрезка , где совпадают знаки функции и второй производной (рис. 2.9). Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.